Координационный номер

Число атомов, молекул или ионов, связанных с молекулой или кристаллом

В химии , кристаллографии и материаловедении координационное число , также называемое лигантией , центрального атома в молекуле или кристалле — это число атомов, молекул или ионов, связанных с ним. Ион/молекула/атом, окружающий центральный ион/молекулу/атом, называется лигандом . Это число определяется несколько иначе для молекул, чем для кристаллов.

Для молекул и многоатомных ионов координационное число атома определяется простым подсчетом других атомов, с которыми он связан (одинарными или множественными связями). ^[1] Например, [Cr(NH ₃ ) ₂ Cl ₂ Br ₂ ] ⁻ имеет Cr ³⁺ в качестве центрального катиона, который имеет координационное число 6 и описывается как гексакоординированный . Обычные координационные числа — 4 , 6 и 8.

Молекулы, многоатомные ионы и координационные комплексы

Шаростержневая модель газообразного U(BH ₄ ) ₄ , которая характеризуется 12-координатным металлическим центром. ^[2]

[Co(NH ₃ ) ₆ ] ³⁺ , который имеет 6-координированный металлический центр с октаэдрической молекулярной геометрией .

Хлор(трифенилфосфин)золото(I) , которое имеет 2-координированный металлический центр.

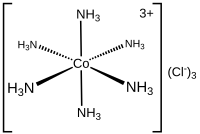
В химии координационное число , первоначально определенное в 1893 году Альфредом Вернером , представляет собой общее число соседей центрального атома в молекуле или ионе. ^{[1] [3]} Это понятие чаще всего применяется к координационным комплексам .

Простые и банальные случаи

Наиболее распространенное координационное число для комплексов переходных металлов d- блока равно 6. Координационное число не различает геометрию таких комплексов, т. е. октаэдрическую или тригонально-призматическую.

Для комплексов переходных металлов координационные числа варьируются от 2 (например, Au ^I в Ph ₃ PAuCl) до 9 (например, Re ^VII в [ReH ₉ ] ²⁻ ). Металлы в f -блоке ( лантаноиды и актиноиды ) могут иметь более высокое координационное число из-за их больших ионных радиусов и наличия большего количества орбиталей для связывания. Координационные числа от 8 до 12 обычно наблюдаются для элементов f -блока. Например, с бидентатными ионами нитрата в качестве лигандов Ce ^IV и Th ^IV образуют 12-координационные ионы [Ce(NO ₃ ) ₆ ] ²⁻ ( церийаммонийнитрат ) и [Th(NO ₃ ) ₆ ] ²⁻ . Когда окружающие лиганды намного меньше центрального атома, возможны даже более высокие координационные числа. Одно исследование вычислительной химии предсказало особенно стабильный PbHe²⁺
₁₅ион, состоящий из центрального иона свинца , координированного не менее чем с 15 атомами гелия. ^[4] Среди фаз Франка-Каспера упаковка металлических атомов может давать координационные числа до 16. ^[5] На противоположной крайности стерическое экранирование может приводить к необычно низким координационным числам. Крайне редкий случай металла, принимающего координационное число 1, происходит в комплексе арилталлия(I) на основе терфенила 2,6-Tipp ₂ C ₆ H ₃ Tl, где Tipp — это 2,4,6-триизопропилфенильная группа. ^[6]

Полигаптолиганды

Координационные числа становятся неоднозначными, когда речь идет о полигаптолигандах. Для π-электронных лигандов, таких как ион циклопентадиенида [C ₅ H ₅ ] ⁻ , алкены и ион циклооктатетраенида [C ₈ H ₈ ] ²⁻ , число соседних атомов в π-электронной системе, которые связываются с центральным атомом, называется гаптичностью . [ ^7] В ферроцене гаптичность η каждого аниона циклопентадиенида равна пяти, Fe( η ⁵ -C ₅ H ₅ ) ₂ . Существуют различные способы назначения вклада, вносимого в координационное число центрального атома железа каждым лигандом циклопентадиенида. Вклад может быть назначен как один, поскольку имеется один лиганд, или как пять, поскольку имеется пять соседних атомов, или как три, поскольку имеется три электронных пары. Обычно берется подсчет электронных пар. ^[8]

Поверхности и реконструкция

Координационные числа хорошо определены для атомов внутри кристаллической решетки : подсчитываются ближайшие соседи во всех направлениях. Число соседей внутреннего атома называется объемным координационным числом . Для поверхностей число соседей более ограничено, поэтому поверхностное координационное число меньше объемного координационного числа. Часто поверхностное координационное число неизвестно или является переменным. ^[9] Поверхностное координационное число также зависит от индексов Миллера поверхности. В объемно-центрированном кубическом (ОЦК) кристалле объемное координационное число равно 8, тогда как для поверхности (100) поверхностное координационное число равно 4. ^[10]

Исследования случаев

Обычный способ определения координационного числа атома — рентгеновская кристаллография . Связанные методы включают нейтронную или электронную дифракцию. ^[11] Координационное число атома можно определить напрямую, подсчитав ближайших соседей.

α-Алюминий имеет правильную кубическую плотноупакованную структуру, ГЦК , где каждый атом алюминия имеет 12 ближайших соседей, 6 в одной плоскости и 3 выше и ниже, а координационный полиэдр представляет собой кубооктаэдр . α-Железо имеет объемно-центрированную кубическую структуру, где каждый атом железа имеет 8 ближайших соседей, расположенных в углах куба.

Графитовый слой, атомы углерода и связи C–C показаны черным цветом.

Два наиболее распространенных аллотропа углерода имеют разные координационные числа. В алмазе каждый атом углерода находится в центре правильного тетраэдра, образованного четырьмя другими атомами углерода, координационное число равно четырем, как и у метана. Графит состоит из двумерных слоев, в которых каждый углерод ковалентно связан с тремя другими углеродами; атомы в других слоях находятся дальше и не являются ближайшими соседями, что дает координационное число 3. ^[12]

структура bcc

Ионы с координационным числом шесть образуют высокосимметричную «структуру каменной соли».

Для химических соединений с регулярной решеткой, таких как хлорид натрия и хлорид цезия , подсчет ближайших соседей дает хорошую картину окружения ионов. В хлориде натрия каждый ион натрия имеет 6 ионов хлора в качестве ближайших соседей (при 276 пм) в углах октаэдра , а каждый ион хлора имеет 6 атомов натрия (также при 276 пм) в углах октаэдра. В хлориде цезия каждый цезий имеет 8 ионов хлора (при 356 пм), расположенных в углах куба , а каждый хлорид имеет восемь ионов цезия (также при 356 пм) в углах куба.

Осложнения

В некоторых соединениях связи металл-лиганд могут не все находиться на одинаковом расстоянии. Например, в PbCl ₂ координационное число Pb ²⁺ можно было бы считать равным семи или девяти, в зависимости от того, какие хлориды назначены в качестве лигандов. Семь хлоридных лигандов имеют расстояния Pb-Cl 280–309 пм. Два хлоридных лиганда находятся на большем расстоянии, с расстояниями Pb-Cl 370 пм. ^[13]

В некоторых случаях используется другое определение координационного числа, которое включает атомы, находящиеся на большем расстоянии, чем ближайшие соседи. Очень широкое определение, принятое Международным союзом кристаллографии (IUCR), гласит, что координационное число атома в кристаллическом теле зависит от модели химической связи и способа расчета координационного числа. ^{[14] [15]}

Некоторые металлы имеют нерегулярные структуры. Например, цинк имеет искаженную гексагональную плотноупакованную структуру. Правильная гексагональная плотноупакованная структура сфер предсказывает, что каждый атом имеет 12 ближайших соседей и треугольный ортобикупольный (также называемый антикубооктаэдром или двойниковым кубооктаэдром) координационный полиэдр. ^{[12] [16]} В цинке есть только 6 ближайших соседей в 266 пм в той же плотноупакованной плоскости с шестью другими, следующими за ближайшими соседями, равноудаленными, по три в каждой из плотноупакованных плоскостей выше и ниже в 291 пм. Считается разумным описывать координационное число как 12, а не как 6. ^[15] Аналогичные соображения можно применить к регулярной объемно-центрированной кубической структуре, где в дополнение к 8 ближайшим соседям есть еще 6, примерно на 15% более удаленных, ^[12] и в этом случае координационное число часто считается равным 14.

Структура NiAs

Многие химические соединения имеют искаженные структуры. Арсенид никеля , NiAs, имеет структуру, в которой атомы никеля и мышьяка имеют 6-координацию. В отличие от хлорида натрия, где ионы хлорида имеют кубическую плотную упаковку, анионы мышьяка имеют гексагональную плотную упаковку. Ионы никеля имеют 6-координацию с искаженным октаэдрическим координационным полиэдром, где колонны октаэдров имеют противоположные грани. Ионы мышьяка не имеют октаэдрической координации, а имеют тригональный призматический координационный полиэдр. Следствием такого расположения является то, что атомы никеля расположены довольно близко друг к другу. Другими соединениями, которые имеют эту структуру или близкородственную ей, являются некоторые сульфиды переходных металлов, такие как FeS и CoS , а также некоторые интерметаллиды. В теллуриде кобальта(II), CoTe, шесть атомов теллура и два атома кобальта находятся на одинаковом расстоянии от центрального атома Co. ^[12]

_{Структура} Fe2O3_​​​

Два других примера часто встречающихся химических веществ — это Fe ₂ O ₃ и TiO ₂ . Fe ₂ O ₃ имеет кристаллическую структуру, которую можно описать как имеющую почти плотно упакованный массив атомов кислорода с атомами железа, заполняющими две трети октаэдрических отверстий. Однако у каждого атома железа есть 3 ближайших соседа и 3 других немного дальше. Структура довольно сложная, атомы кислорода координируются с четырьмя атомами железа, а атомы железа, в свою очередь, разделяют вершины, ребра и грани искаженных октаэдров. ^[12] TiO ₂ имеет структуру рутила . Атомы титана 6-координированы, 2 атома при 198,3 пм и 4 при 194,6 пм, в слегка искаженном октаэдре. Октаэдры вокруг атомов титана разделяют ребра и вершины, образуя трехмерную сеть. Оксидные ионы имеют 3-координаты в тригональной плоской конфигурации. ^[17]

Использование в квазикристаллах, жидкостях и других неупорядоченных системах

Первое координационное число жидкости Леннарда-Джонса

Второе координационное число жидкости Леннарда-Джонса

Координационное число систем с беспорядком не может быть точно определено.

Первое координационное число можно определить с помощью функции радиального распределения g ( r ): ^{[18] [19]} где r ₀ — самое правое положение, начиная с r  = 0, при котором g ( r ) приблизительно равно нулю, r ₁ — первый минимум. Следовательно, это площадь под первым пиком g ( r ). $${\displaystyle n_{1}=4\pi \int _{r_{0}}^{r_{1}}r^{2}g(r)\rho \,dr,}$$

Аналогично определяется второе координационное число : $${\displaystyle n_{2}=4\pi \int _{r_{1}}^{r_{2}}r^{2}g(r)\rho \,dr.}$$

Альтернативные определения координационного числа можно найти в литературе, но по сути основная идея та же. Одно из этих определений следующее: Обозначая положение первого пика как r _p , $${\displaystyle n'_{1}=8\pi \int _{r_{0}}^{r_{p}}r^{2}g(r)\rho \,dr.}$$

Первая координационная оболочка представляет собой сферическую оболочку с радиусом от r ₀ до r ₁ вокруг центральной исследуемой частицы. ^{[20] [21]}

Ссылки

1. IUPAC , Compendium of Chemical Terminology , 2nd ed. («Золотая книга») (1997). Онлайн-исправленная версия: (2006–) «координационное число». doi :10.1351/goldbook.C01331
2. Haaland, Arne; Shorokhov, Dmitry J.; Tutukin, Андрей V.; Volden, Hans Vidar; Swang, Ole; McGrady, G. Sean; Kaltsoyannis, Nikolas; Downs, Anthony J.; Tang, Christina Y.; Turner, John FC (2002). "Молекулярные структуры двух металлических тетракис(тетрагидроборатов), Zr(BH ₄ ) ₄ и U(BH ₄ ) ₄ : равновесные конформации и барьеры для внутреннего вращения трехмостиковых групп BH ₄ ". Неорганическая химия . 41 (25): 6646–6655. doi :10.1021/ic020357z. PMID  12470059.
3. Де, АК (2003). Учебник неорганической химии . New Age International Publishers. стр. 88. ISBN 978-8122413847.
4. Германн, Андреас; Лейн, Маттиас; Швердтфегер, Питер (2007). «Поиск видов с самым высоким координационным числом». Angewandte Chemie International Edition . 46 (14): 2444–7. doi :10.1002/anie.200604148. PMID  17315141.
5. Синха, Ашок К. (1972). «Топологически плотноупакованные структуры сплавов переходных металлов». Прогресс в материаловедении . 15 (2). Elsevier BV: 81–185. doi :10.1016/0079-6425(72)90002-3. ISSN  0079-6425.
6. Нимейер, Марк; Пауэр, Филип П. (1998-05-18). "Синтез и твердотельная структура 2,6-Trip2C6H3Tl (Trip=2,4,6-iPr3C6H2): мономерное соединение арилталлия(I) с однократно координированным атомом таллия". Angewandte Chemie International Edition . 37 (9): 1277–1279. doi :10.1002/(SICI)1521-3773(19980518)37:9<1277::AID-ANIE1277>3.0.CO;2-1. ISSN  1521-3773. PMID  29711226.
7. IUPAC , Compendium of Chemical Terminology , 2nd ed. («Золотая книга») (1997). Онлайн-исправленная версия: (2006–) «hapticity». doi :10.1351/goldbook.H01881
8. Крэбтри, Роберт Х. (2009). Металлоорганическая химия переходных металлов . John Wiley & Sons. ISBN 9780470257623.
9. Де Грэф, Марк; МакГенри, Майкл Э. (2007). Структура материалов: Введение в кристаллографию, дифракцию и симметрию (PDF) . Cambridge University Press. стр. 515. ISBN 978-0-521-65151-6. Архивировано из оригинала (PDF) 29 апреля 2021 г. . Получено 15 марта 2019 г. .
10. "Самые плотно упакованные структуры". Chemistry LibreTexts . 2 октября 2013 г. Получено 28 июля 2020 г.
11. Масса, Вернер (1999). Определение структуры кристаллов (англ. ред.). Springer. стр. 67–92.
12. Уэллс, А. Ф. (1984). Структурная неорганическая химия (5-е изд.). Oxford Science Publications. ISBN 978-0198553700.
13. Уэллс А.Ф. (1984) Структурная неорганическая химия 5-е издание Oxford Science Publications ISBN 0-19-855370-6 
14. "II. Координация атомов". Архивировано из оригинала 2012-06-13 . Получено 2014-11-09 .
15. Mittemeijer, Eric J. (2010). Основы материаловедения: взаимосвязь микроструктуры и свойств с использованием металлов в качестве модельных систем . Springer. ISBN 9783642105005.
16. Piróth, A.; Sólyom, Jenö (2007). Основы физики твердого тела: Том 1: Структура и динамика . Springer. стр. 227. ISBN 9783540726005.
17. Дибольд, Ульрике (2003). «Наука о поверхности диоксида титана». Surface Science Reports . 48 (5–8): 53–229. Bibcode : 2003SurSR..48...53D. doi : 10.1016/S0167-5729(02)00100-0. ISSN  0167-5729.
18. Васеда, И. (1980). Структура некристаллических материалов: жидкости и аморфные твердые тела. Расширенная книжная программа. McGraw-Hill International Book Company. ISBN 978-0-07-068426-3. Получено 16 октября 2020 г. .
19. Vahvaselkä, KS; Mangs, JM (1988). "Исследование рентгеновской дифракции жидкой серы". Physica Scripta . 38 (5): 737. Bibcode : 1988PhyS...38..737V. doi : 10.1088/0031-8949/38/5/017. S2CID  250801367.
20. Toofan, Jahansooz (1994). "Простое выражение между критическим отношением радиусов и координационным числом". Journal of Chemical Education . 71 (2): 147. Bibcode :1994JChEd..71..147T. doi :10.1021/ed071p147 . Получено 3 января 2022 г. .
21. "Errata". Журнал химического образования . 71 (9): 749. 1994. Bibcode :1994JChEd..71..749.. doi : 10.1021/ed071p749 .

Внешние ссылки

• Метеорит Книга-Глоссарий C
• Сайт о координационных числах