Моделирование диода

В электронике моделирование диодов относится к математическим моделям, используемым для аппроксимации фактического поведения реальных диодов, чтобы обеспечить возможность вычислений и анализа цепей. I - V - кривая диода нелинейна .

Очень точная, но сложная физическая модель составляет кривую ВАХ из трех экспонент с немного разной крутизной (т.е. фактором идеальности ), которые соответствуют различным механизмам рекомбинации в устройстве; ^[1] при очень больших и очень малых токах кривая может быть продолжена линейными сегментами (т.е. резистивным поведением).

В относительно хорошем приближении диод моделируется одноэкспоненциальным законом диода Шокли . Эта нелинейность все еще усложняет расчеты в схемах с диодами, поэтому часто используются даже более простые модели.

В данной статье обсуждается моделирование диодов с p-n-переходом , но эти методы могут быть обобщены и на другие твердотельные диоды.

Моделирование большого сигнала

Модель диода Шокли

Уравнение диода Шокли связывает ток диода pn -перехода с напряжением диода . Это соотношение представляет собой вольт-амперную характеристику диода : ${\displaystyle I}$ ${\displaystyle V_{D}}$

${\displaystyle I=I_{S}\left(e^{\frac {V_{D}}{nV_{\text{T}}}}-1\right)}$,

где - ток насыщения или масштабный ток диода (величина тока, который течет при отрицательном значении свыше нескольких , обычно 10 ⁻¹² А). Масштабный ток пропорционален площади поперечного сечения диода. Продолжая символы: - тепловое напряжение ( , около 26 мВ при нормальных температурах), ${\displaystyle I_{S}}$ ${\displaystyle V_{D}}$ ${\displaystyle V_{\text{T}}}$  ${\displaystyle V_{\text{T}}}$ ${\displaystyle kT/q}$и известен как коэффициент идеальности диода (для кремниевых диодов он составляет приблизительно от 1 до 2). ${\displaystyle n}$ ${\displaystyle n}$

Когда формулу можно упростить до: ${\displaystyle V_{D}\gg nV_{\text{T}}}$

${\displaystyle I\approx I_{S}\cdot e^{\frac {V_{D}}{nV_{\text{T}}}}}$.

Это выражение, однако, является лишь приближением более сложной характеристики IV. Его применимость особенно ограничена в случае сверхмелких переходов, для которых существуют лучшие аналитические модели. ^[2]

Пример схемы диод-резистор

Чтобы проиллюстрировать сложности использования этого закона, рассмотрим задачу нахождения напряжения на диоде на рисунке 1.

Рисунок 1: Диодная схема с резистивной нагрузкой.

Поскольку ток, текущий через диод, такой же, как ток во всей цепи, мы можем составить другое уравнение. Согласно законам Кирхгофа , ток, текущий в цепи, равен

${\displaystyle I={\frac {V_{S}-V_{D}}{R}}}$.

Эти два уравнения определяют ток диода и напряжение диода. Чтобы решить эти два уравнения, мы могли бы подставить ток из второго уравнения в первое уравнение, а затем попытаться переставить полученное уравнение так, чтобы получить в терминах . Сложность этого метода заключается в том, что диодный закон нелинеен. Тем не менее, формулу, выражающую непосредственно в терминах без привлечения, можно получить с помощью W -функции Ламберта , которая является обратной функцией , то есть . Это решение обсуждается далее. ${\displaystyle I}$ ${\displaystyle V_{D}}$ ${\displaystyle V_{S}}$ ${\displaystyle I}$ ${\displaystyle V_{S}}$ ${\displaystyle V_{D}}$ ${\displaystyle f(w)=we^{w}}$ ${\displaystyle w=W(f)}$

Явное решение

Явное выражение для тока диода можно получить в терминах W -функции Ламберта (также называемой функцией Омега). ^[3] Ниже приведено руководство по этим манипуляциям. Вводится новая переменная как ${\displaystyle w}$

${\displaystyle w={\frac {I_{S}R}{nV_{\text{T}}}}\left({\frac {I}{I_{S}}}+1\right)}$.

После замен : ${\displaystyle I/I_{S}=e^{V_{D}/nV_{\text{T}}}-1}$

${\displaystyle we^{w}={\frac {I_{S}R}{nV_{\text{T}}}}e^{\frac {V_{D}}{nV_{\text{T}}}}e^{{\frac {I_{S}R}{nV_{\text{T}}}}\left({\frac {I}{I_{S}}}+1\right)}}$

и : ${\displaystyle V_{D}=V_{S}-IR}$

${\displaystyle we^{w}={\frac {I_{S}R}{nV_{\text{T}}}}e^{\frac {V_{S}}{nV_{\text{T}}}}e^{\frac {-IR}{nV_{\text{T}}}}e^{\frac {IRI_{S}}{nV_{\text{T}}I_{S}}}e^{\frac {I_{S}R}{nV_{\text{T}}}}}$

Перестановка диодного закона в терминах w становится:

${\displaystyle we^{w}={\frac {I_{S}R}{nV_{\text{T}}}}e^{\frac {V_{s}+I_{s}R}{nV_{\text{T}}}}}$,

что с использованием функции Ламберта становится ${\displaystyle W}$

${\displaystyle w=W\left({\frac {I_{S}R}{nV_{\text{T}}}}e^{\frac {V_{s}+I_{s}R}{nV_{\text{T}}}}\right)}$.

Окончательное явное решение:

${\displaystyle I={\frac {nV_{\text{T}}}{R}}W\left({\frac {I_{S}R}{nV_{\text{T}}}}e^{\frac {V_{s}+I_{s}R}{nV_{\text{T}}}}\right)-I_{S}}$.

С приближениями (справедливыми для наиболее распространенных значений параметров) и это решение становится ${\displaystyle I_{s}R\ll V_{S}}$ ${\displaystyle I/I_{S}\gg 1}$

${\displaystyle I\approx {\frac {nV_{\text{T}}}{R}}W\left({\frac {I_{S}R}{nV_{\text{T}}}}e^{\frac {V_{s}}{nV_{\text{T}}}}\right)}$.

После определения тока напряжение на диоде можно найти с помощью любого из других уравнений.

Для больших x можно аппроксимировать как . Для обычных физических параметров и сопротивлений будет порядка 10 ⁴⁰ . ${\displaystyle W(x)}$ ${\displaystyle W(x)=\ln x-\ln \ln x+o(1)}$ ${\displaystyle {\frac {I_{S}R}{nV_{\text{T}}}}e^{\frac {V_{s}}{nV_{\text{T}}}}}$

Итеративное решение

Напряжение диода можно найти в терминах для любого конкретного набора значений итеративным методом с использованием калькулятора или компьютера. ^[4] Закон диода переписывается путем деления на и прибавления 1. Закон диода становится ${\displaystyle V_{D}}$ ${\displaystyle V_{S}}$ ${\displaystyle I_{S}}$

${\displaystyle e^{\frac {V_{D}}{nV_{\text{T}}}}={\frac {I}{I_{S}}}+1}$.

Взяв натуральные логарифмы обеих частей, экспонента удаляется, и уравнение принимает вид

${\displaystyle {\frac {V_{D}}{nV_{\text{T}}}}=\ln \left({\frac {I}{I_{S}}}+1\right)}$.

Для любого это уравнение определяет . Однако также должно удовлетворять уравнению закона Кирхгофа, приведенному выше. Это выражение подставляется для получения ${\displaystyle I}$ ${\displaystyle V_{D}}$ ${\displaystyle I}$ ${\displaystyle I}$

${\displaystyle {\frac {V_{D}}{nV_{\text{T}}}}=\ln \left({\frac {V_{S}-V_{D}}{RI_{S}}}+1\right)}$,

или

${\displaystyle V_{D}=nV_{\text{T}}\ln \left({\frac {V_{S}-V_{D}}{RI_{S}}}+1\right)}$.

Напряжение источника — это известное заданное значение, но оно находится на обеих сторонах уравнения, что вынуждает к итеративному решению: начальное значение для угадывается и помещается в правую часть уравнения. Выполняя различные операции на правой стороне, мы приходим к новому значению для . Это новое значение теперь подставляется на правую сторону и так далее. Если эта итерация сходится, значения становятся все ближе и ближе друг к другу по мере продолжения процесса, и мы можем остановить итерацию, когда точность станет достаточной. Как только будет найдено, можно найти из уравнения закона Кирхгофа. ${\displaystyle V_{S}}$ ${\displaystyle V_{D}}$ ${\displaystyle V_{D}}$ ${\displaystyle V_{D}}$ ${\displaystyle V_{D}}$ ${\displaystyle V_{D}}$ ${\displaystyle I}$

Иногда итерационная процедура критически зависит от первой догадки. В этом примере подойдет почти любая первая догадка, скажем . Иногда итерационная процедура вообще не сходится: в этой задаче итерация, основанная на экспоненциальной функции, не сходится, и именно поэтому уравнения были переставлены так, чтобы использовать логарифм. Нахождение сходящейся итерационной формулировки — это искусство, и каждая задача отличается. ${\displaystyle V_{D}=600\,{\text{mV}}}$

Графическое решение

Графическое определение рабочей точки через пересечение характеристики диода с линией резистивной нагрузки.

Графический анализ — это простой способ получить численное решение трансцендентных уравнений, описывающих диод. Как и большинство графических методов, он имеет преимущество в виде простой визуализации. Построив графики кривых I - V , можно получить приближенное решение с любой произвольной степенью точности. Этот процесс является графическим эквивалентом двух предыдущих подходов, которые более поддаются компьютерной реализации.

Этот метод отображает два уравнения тока и напряжения на графике, и точка пересечения двух кривых удовлетворяет обоим уравнениям, давая значение тока, протекающего через цепь, и напряжения на диоде. Рисунок иллюстрирует такой метод.

Кусочно-линейная модель

Кусочно-линейная аппроксимация характеристики диода.

На практике графический метод сложен и непрактичен для сложных схем. Другой метод моделирования диода называется кусочно-линейным (PWL) моделированием . В математике это означает взятие функции и разбиение ее на несколько линейных сегментов. Этот метод используется для аппроксимации характеристической кривой диода как серии линейных сегментов. Реальный диод моделируется как 3 последовательных компонента: идеальный диод, источник напряжения и резистор .

На рисунке показана кривая ВАХ реального диода, аппроксимированная двухсегментной кусочно-линейной моделью. Обычно наклонный сегмент прямой выбирается касательным к кривой диода в точке Q. Тогда наклон этой прямой определяется обратной величиной сопротивления слабого сигнала диода в точке Q.

Математически идеализированный диод

ВАХ идеального диода.

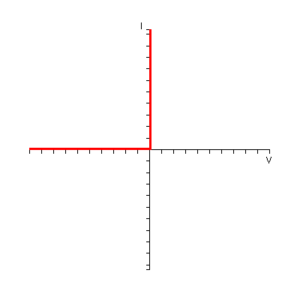
Во-первых, рассмотрим математически идеализированный диод. В таком идеальном диоде, если диод смещен в обратном направлении, ток, протекающий через него, равен нулю. Этот идеальный диод начинает проводить при 0 В, и для любого положительного напряжения течет бесконечный ток, и диод действует как короткое замыкание. Характеристики IV идеального диода показаны ниже:

Идеальный диод последовательно с источником напряжения

Теперь рассмотрим случай, когда мы добавляем источник напряжения последовательно с диодом в форме, показанной ниже:

Идеальный диод с последовательным источником напряжения.

При прямом смещении идеальный диод представляет собой просто короткое замыкание, а при обратном смещении — разомкнутую цепь.

Если анод диода подключен к 0  В, напряжение на катоде будет равно Vt , поэтому потенциал на катоде будет больше, чем потенциал на аноде, и диод будет смещен в обратном направлении. Чтобы заставить диод проводить, напряжение на аноде должно быть доведено до Vt. Эта схема приближается к напряжению включения, присутствующему в реальных диодах. Объединенная вольт-амперная характеристика этой схемы показана ниже:

ВАХ идеального диода с последовательным источником напряжения.

Модель диода Шокли можно использовать для прогнозирования приблизительного значения . ${\displaystyle V_{t}}$

${\displaystyle {\begin{aligned}&I=I_{S}\left(e^{\frac {V_{D}}{n\cdot V_{\text{T}}}}-1\right)\\\Leftrightarrow {}&\ln \left(1+{\frac {I}{I_{S}}}\right)={\frac {V_{D}}{n\cdot V_{\text{T}}}}\\\Leftrightarrow {}&V_{D}=n\cdot V_{\text{T}}\ln \left(1+{\frac {I}{I_{S}}}\right)\approx n\cdot V_{\text{T}}\ln \left({\frac {I}{I_{S}}}\right)\\\Leftrightarrow {}&V_{D}\approx n\cdot V_{\text{T}}\cdot \ln {10}\cdot \log _{10}{\left({\frac {I}{I_{S}}}\right)}\end{aligned}}}$

Используя и : ${\displaystyle n=1}$ ${\displaystyle T=25\,{\text{°C}}}$

${\displaystyle V_{D}\approx 0.05916\cdot \log _{10}{\left({\frac {I}{I_{S}}}\right)}}$

Типичные значения тока насыщения при комнатной температуре:

• ${\displaystyle I_{S}=10^{-12}}$для кремниевых диодов;
• ${\displaystyle I_{S}=10^{-6}}$для германиевых диодов.

Поскольку изменение идет вместе с логарифмом отношения , его значение меняется очень мало при большом изменении отношения. Использование логарифмов по основанию 10 облегчает мышление в порядках величин. ${\displaystyle V_{D}}$ ${\displaystyle {\frac {I}{I_{S}}}}$

Для тока 1,0  мА:

• ${\displaystyle V_{D}\approx 0.53\,{\text{V}}}$для кремниевых диодов (9 порядков);
• ${\displaystyle V_{D}\approx 0.18\,{\text{V}}}$для германиевых диодов (3 порядка).

Для тока 100  мА:

• ${\displaystyle V_{D}\approx 0.65\,{\text{V}}}$для кремниевых диодов (11 порядков);
• ${\displaystyle V_{D}\approx 0.30\,{\text{V}}}$для германиевых диодов (5 порядков).

Для кремниевых диодов обычно используются значения 0,6 или 0,7 вольта. ^[5]

Диод с источником напряжения и токоограничивающим резистором

Последнее, что нужно, — это резистор для ограничения тока, как показано ниже:

Идеальный диод с последовательным источником напряжения и резистором.

ВАХ конечной цепи выглядит следующим образом :

ВАХ идеального диода с последовательным источником напряжения и резистором.

Реальный диод теперь можно заменить комбинированным идеальным диодом, источником напряжения и резистором, и тогда схема будет смоделирована с использованием только линейных элементов. Если наклонный отрезок касается кривой реального диода в точке Q , эта приближенная схема имеет ту же схему малого сигнала в точке Q, что и реальный диод.

Модель с двумя PWL-диодами или 3-линейной PWL

Характеристика IV стандартной модели PWL (отмечена красными треугольниками), как описано выше. Для справки показана стандартная модель диода Шокли (отмечена синими ромбами). Параметры Шокли: I _s = 1e - 12 A, V _t = 0,0258 В

Когда требуется большая точность моделирования характеристики включения диода, модель может быть улучшена путем удвоения стандартной модели PWL. Эта модель использует два кусочно-линейных диода параллельно, как способ более точного моделирования одного диода.

Модель диода PWL с 2 ветвями. Верхняя ветвь имеет более низкое прямое напряжение и более высокое сопротивление. Это позволяет диоду включаться более плавно, и в этом отношении более точно моделирует реальный диод. Нижняя ветвь имеет более высокое прямое напряжение и более низкое сопротивление, что позволяет обеспечить высокий ток при высоком напряжении

График вольт-амперной характеристики этой модели (отмечено красными треугольниками) в сравнении со стандартной моделью диода Шокли (отмечено синими ромбами). Параметры Шокли: I _s = 1e - 12 A, V _t = 0,0258 В

Моделирование малых сигналов

Сопротивление

Используя уравнение Шокли, сопротивление диода при слабом сигнале можно вывести относительно некоторой рабочей точки ( точки Q ), где постоянный ток смещения равен , а приложенное напряжение точки Q равно . ^[6] Для начала находим проводимость диода при слабом сигнале , то есть изменение тока в диоде, вызванное небольшим изменением напряжения на диоде, деленное на это изменение напряжения, а именно: ${\displaystyle r_{D}}$ ${\displaystyle I_{Q}}$ ${\displaystyle V_{Q}}$ ${\displaystyle g_{D}}$

${\displaystyle g_{D}=\left.{\frac {dI}{dV}}\right|_{Q}={\frac {I_{s}}{n\cdot V_{\text{T}}}}e^{\frac {V_{Q}}{n\cdot V_{\text{T}}}}\approx {\frac {I_{Q}}{n\cdot V_{\text{T}}}}}$.

Последнее приближение предполагает, что ток смещения достаточно велик, так что коэффициент 1 в скобках уравнения диода Шокли можно игнорировать. Это приближение является точным даже при довольно малых напряжениях, поскольку тепловое напряжение при 300 К, таким образом, имеет тенденцию быть большим, что означает, что экспонента очень большая. ${\displaystyle I_{Q}}$ ${\displaystyle V_{\text{T}}\approx 25\,{\text{mV}}}$  ${\displaystyle V_{Q}/V_{\text{T}}}$

Учитывая, что сопротивление слабого сигнала является обратной величиной только что найденной проводимости слабого сигнала, сопротивление диода не зависит от переменного тока, но зависит от постоянного тока и определяется как ${\displaystyle r_{D}}$

${\displaystyle r_{D}={\frac {n\cdot V_{\text{T}}}{I_{Q}}}}$.

Емкость

Известно, что заряд в диоде, по которому течет ток, равен ${\displaystyle I_{Q}}$

${\displaystyle Q=I_{Q}\tau _{F}+Q_{J}}$,

где - время прямого прохождения носителей заряда: ^[6] Первый член в заряде - это заряд, проходящий через диод при протекании тока. Второй член - это заряд, хранящийся в самом соединении, когда оно рассматривается как простой конденсатор ; то есть как пара электродов с противоположными зарядами на них. Это заряд, хранящийся на диоде просто в силу наличия напряжения на нем, независимо от того, какой ток он проводит. ${\displaystyle \tau _{F}}$ ${\displaystyle I_{Q}}$

Аналогично, как и прежде, емкость диода представляет собой изменение заряда диода в зависимости от напряжения на диоде:

${\displaystyle C_{D}={\frac {dQ}{dV_{Q}}}={\frac {dI_{Q}}{dV_{Q}}}\tau _{F}+{\frac {dQ_{J}}{dV_{Q}}}\approx {\frac {I_{Q}}{V_{\text{T}}}}\tau _{F}+C_{J}}$,

где — емкость перехода, а первый член называется диффузионной емкостью , поскольку он связан с током, проходящим через переход. ${\displaystyle C_{J}={\frac {dQ_{J}}{dV_{Q}}}}$

Изменение прямого напряжения в зависимости от температуры

Уравнение диода Шокли имеет экспоненту , что привело бы к тому, что прямое напряжение увеличивается с температурой. На самом деле, это, как правило, не так: с ростом температуры ток насыщения увеличивается, и этот эффект доминирует. Таким образом, по мере того, как диод становится горячее , прямое напряжение (для данного тока) уменьшается . ${\displaystyle V_{D}/(kT/q)}$ ${\displaystyle I_{S}}$

Вот некоторые подробные экспериментальные данные, ^[7] которые показывают это для кремниевого диода 1N4005. Фактически, некоторые кремниевые диоды используются в качестве датчиков температуры; например, серия CY7 от OMEGA имеет прямое напряжение 1,02  В в жидком азоте (77  К), 0,54  В при комнатной температуре и 0,29  В при 100 °C. ^[8]

Кроме того, есть небольшое изменение параметра запрещенной зоны материала с температурой. Для светодиодов это изменение запрещенной зоны также изменяет их цвет: они смещаются к синему концу спектра при охлаждении.

Поскольку прямое напряжение диода падает по мере повышения его температуры, это может привести к тепловому разгону из -за перегрузки по току при параллельном включении в схемы биполярных транзисторов (поскольку переход база-эмиттер биполярного транзистора действует как диод), где уменьшение прямого напряжения база-эмиттер приводит к увеличению рассеиваемой мощности коллектора, что, в свою очередь, еще больше снижает требуемое прямое напряжение база-эмиттер.

Смотрите также

• Биполярный транзистор
• Моделирование полупроводниковых приборов

Ссылки

1. B. Van Zeghbroeck (2011). "Pn-переходы: IV-характеристики реальных pn-диодов". Архивировано из оригинала 2021-06-15 . Получено 2020-11-02 .
2. . Popadic, Miloš; Lorito, Gianpaolo; Nanver, Lis K. (2009). "Аналитическая модель I – V характеристик произвольно неглубоких pn переходов". IEEE Transactions on Electron Devices . 56 (1): 116–125. Bibcode :2009ITED...56..116P. doi :10.1109/TED.2008.2009028.
3. Банвелл, TC; Джаякумар, A. (2000). «Точное аналитическое решение для тока через диод с последовательным сопротивлением». Electronics Letters . 36 (4): 291. Bibcode : 2000ElL....36..291B. doi : 10.1049/el:20000301.
4. . AS Sedra и KC Smith (2004). Микроэлектронные схемы (Пятое изд.). Нью-Йорк: Оксфорд. Пример 3.4 стр. 154. ISBN 978-0-19-514251-8.
5. Кал, Сантирам (2004). "Глава 2". Базовая электроника: приборы, схемы и основы ИТ (Раздел 2.5: Модель схемы диода с p-n-переходом, ред.). Prentice-Hall of India Pvt.Ltd. ISBN 978-81-203-1952-3.
6. RC Jaeger и TN Blalock (2004). Проектирование микроэлектронных схем (второе издание). McGraw-Hill. ISBN 978-0-07-232099-2.
7. "1n400x диодное семейство прямое напряжение". www.cliftonlaboratories.com . Clifton Laboratories. 14 апреля 2009 г. Архивировано из оригинала 6 сентября 2013 г. Получено 10 февраля 2019 г.
8. http://www.omega.com/Temperature/pdf/CY7.pdf технический паспорт