Кубооктаэдр — это многогранник с 8 треугольными гранями и 6 квадратными гранями. Кубооктаэдр имеет 12 одинаковых вершин , в каждой из которых сходятся 2 треугольника и 2 квадрата, и 24 одинаковых ребра , каждое из которых отделяет треугольник от квадрата. Таким образом, это квазиправильный многогранник , т. е. архимедово тело , которое не только вершинно-транзитивно , но и рёберно-транзитивно . [1] Он радиально равносторонний. Его двойственный многогранник — ромбический додекаэдр .
Кубооктаэдр можно построить многими способами:
Из всех этих построений кубооктаэдр имеет 14 граней: 8 равносторонних треугольников и 6 квадратов. Он также имеет 24 ребра и 12 вершин. [5]
Декартовы координаты вершин кубооктаэдра с длиной ребра, центрированной в начале координат, следующие: [6]
Площадь поверхности кубооктаэдра можно определить, суммируя все площади его многоугольных граней. Объем кубооктаэдра можно определить, разрезав его на два правильных треугольных купола, суммируя их объемы. Учитывая, что длина ребра , его площадь поверхности и объем равны: [5]
Двугранный угол кубооктаэдра можно вычислить с помощью угла треугольных куполов. Двугранный угол треугольного купола между квадратом и треугольником составляет приблизительно 125°, между квадратом и шестиугольником составляет 54,7°, а между треугольником и шестиугольником составляет 70,5°. Следовательно, двугранный угол кубооктаэдра между квадратом и треугольником на ребре, где прикреплены основания двух треугольных куполов, составляет 54,7° + 70,5°, приблизительно 125°. Следовательно, двугранный угол кубооктаэдра между квадратом и треугольником составляет приблизительно 125°. [7]

Бакминстер Фуллер обнаружил, что кубооктаэдр — единственный многогранник, в котором расстояние между его центром и вершиной такое же, как и расстояние между его ребрами. Другими словами, он имеет одинаковые векторы длины в трехмерном пространстве, известные как векторное равновесие . [8] Жесткие распорки и гибкие вершины кубооктаэдра также могут быть постепенно преобразованы в правильный икосаэдр , правильный октаэдр, правильный тетраэдр. Фуллер назвал это преобразованием джиттербага . [9]
Кубооктаэдр обладает свойством Руперта , означающим, что существует многогранник такого же или большего размера, который может пройти через его отверстие. [10]

Кубооктаэдр является архимедовым телом , то есть это высокосимметричный и полуправильный многогранник, и две или более различных правильных многоугольных граней сходятся в вершине. [11] Кубооктаэдр имеет две симметрии, вытекающие из построений, как было упомянуто выше: та же симметрия, что и у правильного октаэдра или куба, октаэдрическая симметрия , и та же симметрия, что и у правильного тетраэдра, тетраэдрическая симметрия . [12] Многоугольные грани, которые сходятся для каждой вершины, представляют собой два равносторонних треугольника и два квадрата, а вершинная фигура кубооктаэдра равна 3.4.3.4. Двойственным кубооктаэдру является ромбический додекаэдр . [13]
В кубооктаэдре длинный радиус (от центра до вершины) равен длине ребра; таким образом, его длинный диаметр (от вершины до противоположной вершины) равен 2 длинам ребра. [14] Его центр подобен вершине канонической пирамиды: на расстоянии одной длины ребра от всех остальных вершин. (В случае кубооктаэдра центр на самом деле является вершиной 6 квадратных и 8 треугольных пирамид). Эта радиальная равносторонняя симметрия является свойством только нескольких однородных многогранников , включая двумерный шестиугольник , трехмерный кубооктаэдр и четырехмерные 24-ячейковый и 8-ячейковый (тессеракт) . [15] Радиально равносторонние многогранники — это те, которые могут быть построены с их длинными радиусами из равносторонних треугольников, которые встречаются в центре многогранника, каждый из которых вносит два радиуса и ребро. Следовательно, все внутренние элементы, которые встречаются в центре этих многогранников, имеют внутренние грани в виде равносторонних треугольников, как при разбиении кубооктаэдра на 6 квадратных пирамид и 8 тетраэдров.
Каждый из этих радиально равносторонних многогранников также встречается в виде ячеек характерной заполняющей пространство мозаики : мозаики правильных шестиугольников, выпрямленных кубических сот (из чередующихся кубооктаэдров и октаэдров), 24-ячеистых сот и тессерактовых сот , соответственно. [16] Каждая мозаика имеет двойную мозаику ; центры ячеек в мозаике являются вершинами ячеек в ее двойной мозаике. Самая плотная известная правильная упаковка сфер в двух, трех и четырех измерениях использует центры ячеек одной из этих мозаик в качестве центров сфер.
Поскольку кубооктаэдр является радиально равносторонним, его центр находится на расстоянии одной длины ребра от 12 вершин.
Кубооктаэдр делит свой скелет с двумя невыпуклыми однородными многогранниками , кубогемиоктаэдром и октагемиоктаэдром . Эти многогранники построены из скелета кубооктаэдра, в котором четыре шестиугольные плоскости делят пополам его диагональ, пересекая его внутреннюю часть. Добавление шести квадратов или восьми равносторонних треугольников приводит к кубогемикотаэдру или октагемиоктаэдру соответственно. [17]
Кубооктаэдр 2-покрывает тетрагемигексаэдр , который соответственно имеет ту же абстрактную вершинную фигуру (два треугольника и два квадрата: ) и половину вершин, ребер и граней. (Фактическая вершинная фигура тетрагемигексаэдра равна , с множителем , обусловленным крестом.) [18]
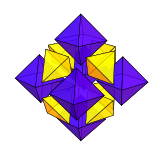
Кубооктаэдр можно разбить на 6 квадратных пирамид и 8 тетраэдров , встречающихся в центральной точке. Это разбиение выражается в тетраэдрально-октаэдрических сотах , где пары квадратных пирамид объединены в октаэдры . [19]

Скелет кубооктаэдра можно представить в виде графа , одного из архимедовых графов . Он имеет 12 вершин и 24 ребра. Это квартикальный граф , который представляет собой четыре вершины, соединяющие каждую вершину. [20]
Граф кубооктаэдра может быть построен как линейный граф куба, что делает его локально линейным графом . [21]
Кубооктаэдр, вероятно, был известен Платону : в «Определениях » Герона цитируются слова Архимеда о том, что Платон знал о теле, состоящем из 8 треугольников и 6 квадратов. [22]