
Линейная диаграмма или линейный график , также известный как кривая диаграмма , [1] представляет собой тип диаграммы , которая отображает информацию в виде ряда точек данных, называемых «маркерами», соединенных прямыми отрезками. [2] Это базовый тип диаграммы, распространенный во многих областях. Он похож на диаграмму рассеяния , за исключением того, что точки измерения упорядочены (обычно по их значению на оси x) и соединены прямыми отрезками. Линейная диаграмма часто используется для визуализации тенденции в данных за интервалы времени — временного ряда — поэтому линия часто рисуется хронологически. В этих случаях они известны как динамические диаграммы .
Некоторые из самых ранних известных линейных диаграмм обычно приписываются Фрэнсису Хоксби , Николаусу Самуэлю Крукиусу , Иоганну Генриху Ламберту и Уильяму Плейфэру . [3]
В экспериментальных науках данные, собранные в ходе экспериментов, часто визуализируются с помощью графика. Например, если собрать данные о скорости объекта в определенные моменты времени, можно визуализировать данные в таблице данных , например, такой:
Такое табличное представление данных является отличным способом отображения точных значений, но оно может помешать обнаружению и пониманию закономерностей в значениях. Кроме того, табличное представление часто ошибочно считается объективным, нейтральным сбором или хранением данных (и в этом смысле может даже ошибочно считаться самими данными), тогда как на самом деле это всего лишь одна из различных возможных визуализаций данных.
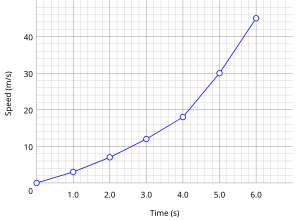
Понимание процесса, описанного данными в таблице, облегчается созданием графика или линейной диаграммы скорости против времени . Такая визуализация представлена на рисунке справа. Эта визуализация может позволить зрителю быстро понять весь процесс с одного взгляда.
Однако эта визуализация может быть неправильно понята, особенно когда она представлена как демонстрация математической функции , которая выражает скорость (зависимую переменную) как функцию времени . Это может быть неправильно понято как демонстрация скорости как переменной, зависящей только от времени. Однако это было бы верно только в случае, если бы на объект воздействовала только постоянная сила, действующая в вакууме.

Диаграммы часто включают в себя наложенную математическую функцию, изображающую наилучшую тенденцию разбросанных данных. Этот слой называется наилучшим слоем, а график, содержащий этот слой, часто называется линейным графиком.
Построить слой «наилучшего соответствия», состоящий из набора отрезков линий, соединяющих соседние точки данных, несложно. Однако такое «наилучшее соответствие» обычно не является идеальным представлением тенденции базовых данных рассеяния по следующим причинам:
В любом случае наиболее подходящий слой может выявить тенденции в данных. Кроме того, измерения, такие как градиент или площадь под кривой, могут быть выполнены визуально, что приводит к большему количеству выводов или результатов из таблицы данных.
Настоящий слой наилучшего соответствия должен отображать непрерывную математическую функцию, параметры которой определяются с помощью подходящей схемы минимизации ошибок, которая соответствующим образом взвешивает ошибку в значениях данных. Такая функциональность подгонки кривой часто встречается в графическом программном обеспечении или электронных таблицах . Кривые наилучшего соответствия могут варьироваться от простых линейных уравнений до более сложных квадратичных, полиномиальных, экспоненциальных и периодических кривых. [4]
{{cite book}}: |work=проигнорировано ( помощь )