В физике твердого тела функция выхода (иногда пишется как функция работы ) — это минимальная термодинамическая работа (т. е. энергия), необходимая для удаления электрона из твердого тела в точку в вакууме непосредственно за пределами поверхности твердого тела. Здесь «непосредственно» означает, что конечное положение электрона находится далеко от поверхности в атомном масштабе, но все еще слишком близко к твердому телу, чтобы на него влияли окружающие электрические поля в вакууме. Функция выхода не является характеристикой объемного материала, а скорее свойством поверхности материала (зависящим от кристаллической грани и загрязнения).
Работа выхода W для данной поверхности определяется разностью [1]
где − e — заряд электрона , ϕ — электростатический потенциал в вакууме вблизи поверхности, а E F — уровень Ферми ( электрохимический потенциал электронов) внутри материала. Член − eϕ — энергия покоящегося электрона в вакууме вблизи поверхности.

На практике E F напрямую управляется напряжением, приложенным к материалу через электроды, а работа выхода, как правило, является фиксированной характеристикой поверхностного материала. Следовательно, это означает, что при приложении напряжения к материалу электростатический потенциал ϕ, создаваемый в вакууме, будет несколько ниже приложенного напряжения, причем эта разница зависит от работы выхода поверхности материала. Переставляя приведенное выше уравнение, получаем
где V = − E F / e — напряжение материала (измеренное вольтметром через присоединенный электрод) относительно электрического заземления , которое определяется как имеющее нулевой уровень Ферми. Тот факт, что ϕ зависит от поверхности материала, означает, что пространство между двумя разнородными проводниками будет иметь встроенное электрическое поле , когда эти проводники находятся в полном равновесии друг с другом (электрически замкнуты друг на друга и имеют равные температуры).
Работа выхода относится к удалению электрона в положение, которое достаточно далеко от поверхности (много нм), чтобы можно было пренебречь силой между электроном и его зарядом изображения на поверхности. [1] Электрон также должен находиться близко к поверхности по сравнению с ближайшим краем грани кристалла или любым другим изменением в структуре поверхности, таким как изменение состава материала, поверхностное покрытие или реконструкция. Встроенное электрическое поле, которое является результатом этих структур, и любое другое окружающее электрическое поле, присутствующее в вакууме, исключаются при определении работы выхода. [2]
Некоторые физические явления очень чувствительны к значению функции выхода. Наблюдаемые данные этих эффектов могут быть подогнаны к упрощенным теоретическим моделям, что позволяет извлечь значение функции выхода. Эти феноменологически извлеченные функции выхода могут немного отличаться от термодинамического определения, данного выше. Для неоднородных поверхностей функция выхода меняется от места к месту, и разные методы будут давать разные значения типичной «функции выхода», поскольку они усредняют или выбирают по-разному среди микроскопических функций выхода. [9]
Разработано много методов, основанных на различных физических эффектах, для измерения электронной работы выхода образца. Можно выделить две группы экспериментальных методов измерения работы выхода: абсолютные и относительные.
Работа выхода важна в теории термоэлектронной эмиссии , где тепловые флуктуации обеспечивают достаточно энергии для «испарения» электронов из горячего материала (называемого «эмиттером») в вакуум. Если эти электроны поглощаются другим, более холодным материалом (называемым коллектором ) , то будет наблюдаться измеримый электрический ток . Термоэлектронная эмиссия может использоваться для измерения работы выхода как горячего эмиттера, так и холодного коллектора. Как правило, эти измерения включают подгонку под закон Ричардсона , и поэтому они должны проводиться в режиме низкой температуры и низкого тока, где эффекты пространственного заряда отсутствуют.
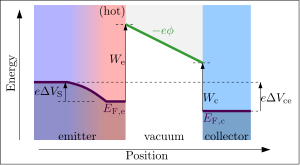
Для того чтобы перейти от горячего эмиттера к вакууму, энергия электрона должна превышать уровень Ферми эмиттера на величину
определяется просто термоионной работой выхода эмиттера. Если электрическое поле приложено к поверхности эмиттера, то все выходящие электроны будут ускорены от эмиттера и поглощены материалом, к которому приложено электрическое поле. Согласно закону Ричардсона, плотность излучаемого тока (на единицу площади эмиттера), J e (A/м 2 ), связана с абсолютной температурой эмиттера T e следующим уравнением:
где k — постоянная Больцмана , а константа пропорциональности A e — постоянная Ричардсона излучателя. В этом случае зависимость J e от T e может быть подогнана так, чтобы получить W e .
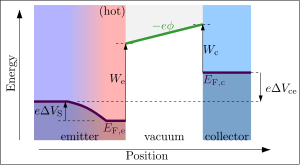
Эту же установку можно использовать для измерения работы выхода в коллекторе, просто регулируя приложенное напряжение. Если вместо этого приложить электрическое поле вдали от эмиттера, то большинство электронов, идущих от эмиттера, просто отразятся обратно в эмиттер. Только электроны с самой высокой энергией будут иметь достаточно энергии, чтобы достичь коллектора, и высота потенциального барьера в этом случае зависит от работы выхода коллектора, а не эмиттера.
Ток по-прежнему подчиняется закону Ричардсона. Однако в этом случае высота барьера не зависит от W e . Высота барьера теперь зависит от работы выхода коллектора, а также от любых дополнительных приложенных напряжений: [11]
где W c — термоионная работа коллектора, Δ V ce — приложенное напряжение коллектор–эмиттер, а Δ V S — напряжение Зеебека в горячем эмиттере (влияние Δ V S часто опускается, так как это небольшой вклад порядка 10 мВ). Результирующая плотность тока J c через коллектор (на единицу площади коллектора) снова определяется законом Ричардсона , за исключением того, что теперь
где A — константа типа Ричардсона, которая зависит от материала коллектора, но может также зависеть от материала эмиттера и геометрии диода. В этом случае зависимость J c от T e или от Δ V ce может быть подогнана для получения W c .
Этот метод задерживающего потенциала является одним из самых простых и старых методов измерения работы выхода и имеет преимущество, поскольку измеряемый материал (коллектор) не обязан выдерживать высокие температуры.
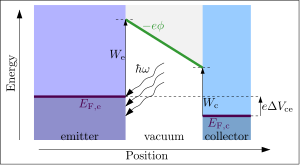
Фотоэлектрическая работа выхода — это минимальная энергия фотона , необходимая для освобождения электрона из вещества в фотоэлектрическом эффекте . Если энергия фотона больше, чем работа выхода вещества, происходит фотоэлектрическая эмиссия , и электрон освобождается с поверхности. Подобно термоионному случаю, описанному выше, освобожденные электроны могут быть извлечены в коллектор и создать обнаруживаемый ток, если электрическое поле приложено к поверхности эмиттера. Избыточная энергия фотона приводит к освобождению электрона с ненулевой кинетической энергией. Ожидается, что минимальная энергия фотона, необходимая для освобождения электрона (и генерации тока), равна
где W e — работа выхода эмиттера.
Фотоэлектрические измерения требуют большой осторожности, поскольку неправильно спроектированная экспериментальная геометрия может привести к ошибочному измерению работы выхода. [9] Это может быть причиной большого разброса значений работы выхода в научной литературе. Более того, минимальная энергия может вводить в заблуждение в материалах, где нет реальных электронных состояний на уровне Ферми, доступных для возбуждения. Например, в полупроводнике минимальная энергия фотона будет фактически соответствовать краю валентной зоны, а не работе выхода. [12]
Конечно, фотоэффект может быть использован в режиме замедления, как в описанном выше термоионном аппарате. В случае замедления вместо этого измеряется работа выхода темного коллектора.

Метод зонда Кельвина основан на обнаружении электрического поля (градиента в ϕ ) между материалом образца и материалом зонда. Электрическое поле может изменяться напряжением Δ V sp , которое прикладывается к зонду относительно образца. Если напряжение выбрано таким образом, что электрическое поле устраняется (условие плоского вакуума), то
Поскольку экспериментатор контролирует и знает Δ V sp , то нахождение состояния плоского вакуума дает непосредственно разницу в работе выхода между двумя материалами. Единственный вопрос заключается в том, как обнаружить состояние плоского вакуума? Обычно электрическое поле обнаруживается путем изменения расстояния между образцом и зондом. Когда расстояние изменяется, но Δ V sp сохраняется постоянным, ток будет течь из-за изменения емкости . Этот ток пропорционален электрическому полю вакуума, и поэтому, когда электрическое поле нейтрализуется, ток не будет течь.
Хотя метод зонда Кельвина измеряет только разницу в работе выхода, можно получить абсолютную работу выхода, сначала откалибровав зонд по эталонному материалу (с известной работой выхода), а затем используя тот же зонд для измерения желаемого образца. [10] Метод зонда Кельвина можно использовать для получения карт работы выхода поверхности с чрезвычайно высоким пространственным разрешением, используя острый наконечник зонда (см. Силовой микроскоп зонда Кельвина ).
Работа выхода зависит от конфигураций атомов на поверхности материала. Например, на поликристаллическом серебре работа выхода составляет 4,26 эВ, но на кристаллах серебра она варьируется для разных граней кристалла, например, грань (100) : 4,64 эВ, грань (110) : 4,52 эВ, грань (111) : 4,74 эВ. [13] Диапазоны для типичных поверхностей показаны в таблице ниже. [14]
Из-за сложностей, описанных в разделе моделирования ниже, трудно теоретически предсказать работу выхода с точностью. Однако были выявлены различные тенденции. Работа выхода имеет тенденцию быть меньше для металлов с открытой решеткой, [ необходимо разъяснение ] и больше для металлов, в которых атомы плотно упакованы. Она несколько выше на плотных гранях кристалла, чем на открытых гранях кристалла, также в зависимости от реконструкций поверхности для данной грани кристалла.
Работа выхода зависит не только от «внутреннего уровня вакуума» внутри материала (т. е. его среднего электростатического потенциала), но и от образования на поверхности двойного электрического слоя атомного масштаба. [7] Этот поверхностный электрический диполь создает скачок электростатического потенциала между материалом и вакуумом.
За поверхностный электрический диполь отвечают различные факторы. Даже при полностью чистой поверхности электроны могут немного распространяться в вакууме, оставляя после себя слегка положительно заряженный слой материала. Это в первую очередь происходит в металлах, где связанные электроны не сталкиваются с жестким потенциалом стенки на поверхности, а скорее с постепенным нарастающим потенциалом из-за притяжения заряда изображения . Величина поверхностного диполя зависит от детального расположения атомов на поверхности материала, что приводит к изменению работы выхода для различных граней кристалла.

В полупроводнике работа выхода чувствительна к уровню легирования на поверхности полупроводника. Поскольку легирование вблизи поверхности также может контролироваться электрическими полями , работа выхода полупроводника также чувствительна к электрическому полю в вакууме.
Причина этой зависимости в том, что, как правило, уровень вакуума и край зоны проводимости сохраняют фиксированное расстояние независимо от легирования. Это расстояние называется сродством к электрону (обратите внимание, что оно имеет иное значение, чем сродство к электрону в химии); например, в кремнии сродство к электрону составляет 4,05 эВ. [16] Если сродство к электрону E EA и уровень Ферми поверхности, привязанный к зоне E F - E C, известны, то работа выхода определяется как
где E C берется на поверхности.
Из этого можно было бы ожидать, что легированием основной массы полупроводника можно настроить работу выхода. В действительности, однако, энергии зон вблизи поверхности часто прикрепляются к уровню Ферми из-за влияния поверхностных состояний . [17] Если плотность поверхностных состояний велика, то работа выхода полупроводника будет демонстрировать очень слабую зависимость от легирования или электрического поля. [18]
Теоретическое моделирование функции выхода затруднено, поскольку точная модель требует тщательного рассмотрения как электронных многочастичных эффектов , так и поверхностной химии ; обе эти темы сами по себе уже сложны.
Одной из самых ранних успешных моделей для тенденций работы выхода металлов была модель желе [19] , которая допускала колебания электронной плотности вблизи резкой поверхности (они похожи на фриделевские колебания ), а также хвост электронной плотности, простирающийся за пределы поверхности. Эта модель показала, почему плотность электронов проводимости (представленная радиусом Вигнера-Зейтца r s ) является важным параметром при определении работы выхода.
Модель желе является лишь частичным объяснением, поскольку ее предсказания все еще показывают значительное отклонение от реальных рабочих функций. Более поздние модели были сосредоточены на включении более точных форм электронного обмена и эффектов корреляции, а также на включении зависимости от кристаллической грани (это требует включения фактической атомной решетки, что пренебрегается в модели желе). [7] [20]
Поведение электронов в металлах меняется в зависимости от температуры и в значительной степени отражается в работе выхода электронов. Теоретическая модель для прогнозирования температурной зависимости работы выхода электронов, разработанная Рахеми и др. [21], объясняет лежащий в основе механизм и предсказывает эту температурную зависимость для различных кристаллических структур с помощью вычисляемых и измеримых параметров. В общем, по мере повышения температуры EWF уменьшается с помощью и является вычисляемым свойством материала, которое зависит от кристаллической структуры (например, ОЦК, ГЦК). — работа выхода электронов при T=0, и она постоянна на протяжении всего изменения.
Для быстрой справки о значениях работы выхода элементов: