Автомат Pushdown

Тип автомата

Классы автоматов

В теории вычислений , разделе теоретической информатики , магазинный автомат ( PDA ) — это тип автомата , использующий стек .

Магазинные автоматы используются в теориях о том, что может быть вычислено машинами. Они более эффективны, чем конечные автоматы , но менее эффективны, чем машины Тьюринга (см. ниже). Детерминированные магазинные автоматы могут распознавать все детерминированные контекстно-свободные языки , в то время как недетерминированные могут распознавать все контекстно-свободные языки , причем первые часто используются при проектировании синтаксических анализаторов .

Термин «pushdown» относится к тому факту, что стек можно рассматривать как «выталкиваемый вниз», как поднос в кафе, поскольку операции никогда не работают с элементами, отличными от верхнего элемента. Автомат стека , напротив, позволяет получать доступ к более глубоким элементам и выполнять операции с ними. Автоматы стека могут распознавать строго больший набор языков, чем автоматы pushdown. ^[1] Вложенный автомат стека обеспечивает полный доступ, а также позволяет стекированным значениям быть целыми подстеками, а не просто отдельными конечными символами.

Неформальное описание

Схема автомата с магазинной крышкой

Конечный автомат просто смотрит на входной сигнал и текущее состояние: у него нет стека для работы, и поэтому он не может получить доступ к предыдущим значениям входа. Он может только выбрать новое состояние, результат перехода. Автомат с магазином (PDA) отличается от конечного автомата двумя способами:

1. Он может использовать верхнюю часть стека, чтобы решить, какой переход следует выполнить.
2. Он может манипулировать стеком в рамках выполнения перехода.

Магазинный автомат считывает заданную входную строку слева направо. На каждом шаге он выбирает переход, индексируя таблицу по входному символу, текущему состоянию и символу наверху стека. Магазинный автомат также может манипулировать стеком в рамках выполнения перехода. Манипуляция может заключаться в том, чтобы поместить определенный символ наверх стека или вытащить его с вершины стека. Автомат может также игнорировать стек и оставить его таким, какой он есть.

В совокупности: при наличии входного символа, текущего состояния и символа стека автомат может выполнить переход в другое состояние и при необходимости манипулировать стеком (вставлять или выталкивать его).

Если в каждой ситуации возможно не более одного такого действия перехода, то автомат называется детерминированным магазинным автоматом (DPDA) . В общем случае, если возможны несколько действий, то автомат называется общим или недетерминированным PDA . Заданная входная строка может привести недетерминированный магазинный автомат к одной из нескольких последовательностей конфигураций; если одна из них приводит к принимающей конфигурации после чтения полной входной строки, то говорят, что последняя принадлежит языку, принимаемому автоматом .

Формальное определение

Мы используем стандартную формальную языковую нотацию: обозначает множество строк конечной длины по алфавиту , а обозначает пустую строку . ${\displaystyle \Gamma ^{*}}$ ${\displaystyle \Gamma }$ ${\displaystyle \varepsilon }$

PDA формально определяется как 7-кортеж:

${\displaystyle M=(Q,\Sigma ,\Gamma ,\delta ,q_{0},Z,F)}$где

• ${\displaystyle Q}$это конечный набор состояний
• ${\displaystyle \Sigma }$— это конечный набор, который называется входным алфавитом.
• ${\displaystyle \Gamma }$это конечное множество, которое называется стековым алфавитом
• ${\displaystyle \delta }$является конечным подмножеством , отношение перехода ${\displaystyle Q\times (\Sigma \cup \{\varepsilon \})\times \Gamma \times Q\times \Gamma ^{*}}$
• ${\displaystyle q_{0}\in Q}$это начальное состояние
• ${\displaystyle Z\in \Gamma }$это начальный символ стека
• ${\displaystyle F\subseteq Q}$это набор принимающих состояний

Элемент — это переход . Он имеет предполагаемое значение, что , в состоянии , на входе и с самым верхним символом стека, может читать , изменять состояние на , выталкивать , заменяя его нажатием . Компонент отношения перехода используется для формализации того, что КПК может либо читать букву из входа, либо продолжать работу, оставляя вход нетронутым. ^{[ необходима цитата ]} ${\displaystyle (p,a,A,q,\alpha )\in \delta }$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle p\in Q}$ ${\displaystyle a\in \Sigma \cup \{\varepsilon \}}$ ${\displaystyle A\in \Gamma }$ ${\displaystyle a}$ ${\displaystyle q}$ ${\displaystyle A}$ ${\displaystyle \alpha \in \Gamma ^{*}}$ ${\displaystyle (\Sigma \cup \{\varepsilon \})}$

Во многих текстах ^{[2] : 110} отношение перехода заменяется (эквивалентной) формализацией, где

• ${\displaystyle \delta }$— это функция перехода , отображающая конечные подмножества ${\displaystyle Q\times (\Sigma \cup \{\varepsilon \})\times \Gamma }$ ${\displaystyle Q\times \Gamma ^{*}}$

Здесь содержатся все возможные действия в состоянии с на стеке, при чтении на входе. Например, пишется точно когда потому что . Обратите внимание, что конечность в этом определении существенна. ${\displaystyle \delta (p,a,A)}$ ${\displaystyle p}$ ${\displaystyle A}$ ${\displaystyle a}$ ${\displaystyle \delta (p,a,A)=\{(q,BA)\}}$ ${\displaystyle (q,BA)\in \{(q,BA)\},(q,BA)\in \delta (p,a,A),}$ ${\displaystyle ((p,a,A),\{(q,BA)\})\in \delta }$

Вычисления

шаг автомата толкания

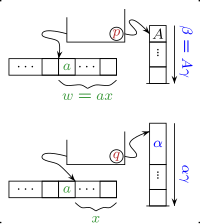
Для формализации семантики магазинного автомата вводится описание текущей ситуации. Любой 3-кортеж называется мгновенным описанием (ID) , которое включает текущее состояние, часть входной ленты, которая не была прочитана, и содержимое стека (самый верхний символ записан первым). Отношение перехода определяет отношение шага для мгновенных описаний. Для инструкции существует шаг , для каждого и каждого . ${\displaystyle (p,w,\beta )\in Q\times \Sigma ^{*}\times \Gamma ^{*}}$ ${\displaystyle M}$ ${\displaystyle \delta }$ ${\displaystyle \vdash _{M}}$ ${\displaystyle M}$ ${\displaystyle (p,a,A,q,\alpha )\in \delta }$ ${\displaystyle (p,ax,A\gamma )\vdash _{M}(q,x,\alpha \gamma )}$ ${\displaystyle x\in \Sigma ^{*}}$ ${\displaystyle \gamma \in \Gamma ^{*}}$

В общем случае магазинные автоматы недетерминированы, что означает, что в данном мгновенном описании может быть несколько возможных шагов. Любой из этих шагов может быть выбран в вычислении. С приведенным выше определением на каждом шаге всегда выталкивается один символ (верхушка стека), заменяя его необходимым количеством символов. Как следствие, ни один шаг не определен, когда стек пуст. ${\displaystyle (p,w,\beta )}$

Вычисления магазинного автомата представляют собой последовательности шагов. Вычисление начинается в начальном состоянии с начальным символом стека на стеке и строкой на входной ленте, таким образом, с начальным описанием . Существует два режима принятия. Магазинный автомат либо принимает по конечному состоянию, что означает, что после чтения его ввода автомат достигает принимающего состояния (в ), либо принимает по пустому стеку ( ), что означает, что после чтения его ввода автомат очищает свой стек. Первый режим принятия использует внутреннюю память (состояние), второй — внешнюю память (стек). ${\displaystyle q_{0}}$ ${\displaystyle Z}$ ${\displaystyle w}$ ${\displaystyle (q_{0},w,Z)}$ ${\displaystyle F}$ ${\displaystyle \varepsilon }$

Формально определяется

1. ${\displaystyle L(M)=\{w\in \Sigma ^{*}|(q_{0},w,Z)\vdash _{M}^{*}(f,\varepsilon ,\gamma )}$с и (конечное состояние) ${\displaystyle f\in F}$ ${\displaystyle \gamma \in \Gamma ^{*}\}}$
2. ${\displaystyle N(M)=\{w\in \Sigma ^{*}|(q_{0},w,Z)\vdash _{M}^{*}(q,\varepsilon ,\varepsilon )}$с (пустой стек) ${\displaystyle q\in Q\}}$

Здесь представлено рефлексивное и транзитивное замыкание шагового отношения, означающего любое количество последовательных шагов (ноль, один или более). ${\displaystyle \vdash _{M}^{*}}$ ${\displaystyle \vdash _{M}}$

Для каждого отдельного магазинного автомата эти два языка не должны иметь никакой связи: они могут быть равны, но обычно это не так. Спецификация автомата должна также включать предполагаемый режим принятия. Применительно ко всем магазинным автоматам оба условия принятия определяют одно и то же семейство языков.

Теорема. Для каждого магазинного автомата можно построить магазинный автомат такой, что , и наоборот, для каждого магазинного автомата можно построить магазинный автомат такой, что ${\displaystyle M}$ ${\displaystyle M'}$ ${\displaystyle L(M)=N(M')}$ ${\displaystyle M}$ ${\displaystyle M'}$ ${\displaystyle N(M)=L(M')}$

Пример

Ниже приведено формальное описание КПК, распознающего язык по конечному состоянию: ${\displaystyle \{0^{n}1^{n}\mid n\geq 0\}}$

КПК для (по конечному состоянию) ${\displaystyle \{0^{n}1^{n}\mid n\geq 0\}}$

${\displaystyle M=(Q,\ \Sigma ,\ \Gamma ,\ \delta ,\ q_{0},\ Z,\ F)}$, где

• говорится: ${\displaystyle Q=\{p,q,r\}}$
• входной алфавит: ${\displaystyle \Sigma =\{0,1\}}$
• стековый алфавит: ${\displaystyle \Gamma =\{A,Z\}}$
• начальное состояние: ${\displaystyle q_{0}=p}$
• начальный символ стека: Z
• принимающие государства: ${\displaystyle F=\{r\}}$

Отношение перехода состоит из следующих шести инструкций: ${\displaystyle \delta }$

${\displaystyle (p,0,Z,p,AZ)}$,

${\displaystyle (p,0,A,p,AA)}$,

${\displaystyle (p,\epsilon ,Z,q,Z)}$,

${\displaystyle (p,\epsilon ,A,q,A)}$,

${\displaystyle (q,1,A,q,\epsilon )}$, и

${\displaystyle (q,\epsilon ,Z,r,Z)}$.

На словах первые две инструкции говорят, что в состоянии p в любой момент времени символСчитывается 0 , в стек помещается один A. Помещение символа A поверх другого A формализуется как замена верхнего A на AA (и аналогично для помещения символа A поверх Z ).

Третья и четвертая инструкции говорят, что в любой момент автомат может перейти из состояния p в состояние q .

Пятая инструкция гласит, что в состоянии q для каждого символа1 прочитано, одна буква А выбита.

Наконец, шестая инструкция гласит , что машина может перейти из состояния q в принимающее состояние r только в том случае, если стек состоит из одного Z.

Кажется, нет общепринятого представления для PDA. Здесь мы изобразили инструкцию ребром из состояния p в состояние q , помеченным (читай a ; замени A на ). ${\displaystyle (p,a,A,q,\alpha )}$ ${\displaystyle a;A/\alpha }$ ${\displaystyle \alpha }$

Объяснение

принятие вычисления для0011

Ниже показано, как вышеуказанный PDA вычисляет различные входные строки. Нижний индекс M из символа шага здесь опущен. ${\displaystyle \vdash }$

1. Входная строка = 0011. Существуют различные вычисления, в зависимости от момента перехода из состояния p в состояние q . Только одно из них является приемным.
   1. ${\displaystyle (p,0011,Z)\vdash (q,0011,Z)\vdash (r,0011,Z)}$
      Конечное состояние — принятие, но входные данные таким образом не принимаются, поскольку они не были прочитаны.
   2. ${\displaystyle (p,0011,Z)\vdash (p,011,AZ)\vdash (q,011,AZ)}$
      Дальнейшие шаги невозможны.
   3. ${\displaystyle (p,0011,Z)\vdash (p,011,AZ)\vdash (p,11,AAZ)\vdash (q,11,AAZ)\vdash (q,1,AZ)\vdash (q,\epsilon ,Z)\vdash (r,\epsilon ,Z)}$
      Принятие вычислений: завершается в состоянии принятия, пока все входные данные считаны.
2. Входная строка = 00111. Опять же, есть различные вычисления. Ни одно из них не принимается.
   1. ${\displaystyle (p,00111,Z)\vdash (q,00111,Z)\vdash (r,00111,Z)}$
      Конечное состояние — принятие, но входные данные таким образом не принимаются, поскольку они не были прочитаны.
   2. ${\displaystyle (p,00111,Z)\vdash (p,0111,AZ)\vdash (q,0111,AZ)}$
      Дальнейшие шаги невозможны.
   3. ${\displaystyle (p,00111,Z)\vdash (p,0111,AZ)\vdash (p,111,AAZ)\vdash (q,111,AAZ)\vdash (q,11,AZ)\vdash (q,1,Z)\vdash (r,1,Z)}$
      Конечное состояние — принятие, но входные данные не принимаются таким образом, поскольку они не были (полностью) прочитаны.

Контекстно-свободные языки

Каждая контекстно-свободная грамматика может быть преобразована в эквивалентный недетерминированный магазинный автомат. Процесс вывода грамматики моделируется самым левым способом. Там, где грамматика переписывает нетерминал, PDA берет самый верхний нетерминал из своего стека и заменяет его правой частью грамматического правила ( expand ). Там, где грамматика генерирует терминальный символ, PDA считывает символ из ввода, когда он является самым верхним символом в стеке ( match ). В некотором смысле стек PDA содержит необработанные данные грамматики, соответствующие предварительному обходу дерева вывода.

Технически, учитывая контекстно-свободную грамматику, PDA имеет единственное состояние 1, а его отношение перехода строится следующим образом.

1. ${\displaystyle (1,\varepsilon ,A,1,\alpha )}$для каждого правила ( развернуть ) ${\displaystyle A\to \alpha }$
2. ${\displaystyle (1,a,a,1,\varepsilon )}$для каждого терминального символа ( совпадение ) ${\displaystyle a}$

КПК принимает пустой стек. Его начальный символ стека — это начальный символ грамматики. ^[3]

Для контекстно-свободной грамматики в нормальной форме Грейбаха определение (1,γ) ∈ δ(1, a , A ) для каждого правила грамматики A → a γ также дает эквивалентный недетерминированный магазинный автомат. ^{[2] : 115}

Обратное, найти грамматику для данного PDA, не так просто. Хитрость в том, чтобы закодировать два состояния PDA в нетерминалы грамматики.

Теорема. Для каждого магазинного автомата можно построить контекстно-свободную грамматику, такую ​​что . ^{[2] : 116} ${\displaystyle M}$ ${\displaystyle G}$ ${\displaystyle N(M)=L(G)}$

Язык строк, принимаемый детерминированным магазинным автоматом (DPDA), называется детерминированным контекстно-свободным языком . Не все контекстно-свободные языки являются детерминированными. ^{[примечание 1]} Как следствие, DPDA является строго более слабым вариантом PDA. Даже для регулярных языков существует проблема взрывного роста размера: для любой рекурсивной функции и для произвольно больших целых чисел существует PDA размера, описывающего регулярный язык, наименьший DPDA которого имеет не менее состояний. ^[5] Для многих нерегулярных PDA любой эквивалентный DPDA потребовал бы неограниченного числа состояний. ${\displaystyle f}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle f(n)}$

Конечный автомат с доступом к двум стекам является более мощным устройством, эквивалентным по мощности машине Тьюринга . ^{[2] : 171} Линейный ограниченный автомат является устройством, которое является более мощным, чем магазинный автомат, но менее мощным, чем машина Тьюринга. ^{[примечание 2]}

Машины Тьюринга

Магазинный автомат вычислительно эквивалентен «ограниченной» машине Тьюринга (TM) с двумя лентами, которая ограничена следующим образом: на первой ленте TM может только считывать входные данные и перемещаться слева направо (она не может вносить изменения). На второй ленте он может только «вталкивать» и «выталкивать» данные. Или, что эквивалентно, он может читать, записывать и перемещаться влево и вправо с ограничением, что единственное действие, которое он может выполнить на каждом шаге, — это либо удалить самый левый символ в строке (pop), либо добавить дополнительный символ слева к самому левому символу в строке (push).

То, что PDA слабее TM, можно объяснить тем, что процедура «pop» удаляет некоторые данные. Чтобы сделать PDA таким же сильным, как TM, нам нужно где-то сохранить данные, потерянные при «pop». Мы можем добиться этого, введя второй стек. В модели TM PDA из последнего абзаца это эквивалентно TM с 3 лентами, где первая лента является входной лентой только для чтения, а 2-я и 3-я ленты являются лентами «push and pop» (стек). Для того чтобы такой PDA мог имитировать любую заданную TM, мы передаем вход PDA на первую ленту, оставляя оба стека пустыми. Затем он продолжает проталкивать весь вход с входной ленты на первый стек. Когда весь ввод переносится в 1-й стек, теперь мы действуем как обычный TM, где перемещение вправо по ленте соответствует извлечению символа из 1-го стека и вставке (возможно, обновленного) символа во второй стек, а перемещение влево соответствует извлечению символа из 2-го стека и вставке (возможно, обновленного) символа в первый стек. Таким образом, у нас есть КПК с 2 стеками, который может имитировать любой TM.

Обобщение

Обобщенный магазинный автомат (GPDA) — это КПК, который записывает целую строку известной длины в стек или удаляет целую строку из стека за один шаг.

Формально GPDA определяется как кортеж из 6 элементов:

${\displaystyle M=(Q,\ \Sigma ,\ \Gamma ,\ \delta ,\ q_{0},\ F)}$

где , и ⁠ ⁠ определяются так же, как КПК. ${\displaystyle Q,\Sigma \,,\Gamma \,,q_{0}}$ ${\displaystyle F}$

${\displaystyle \,\delta }$: ${\displaystyle Q\times \Sigma _{\epsilon }\times \Gamma ^{*}\longrightarrow P(Q\times \Gamma ^{*})}$

— это функция перехода.

Правила вычислений для GPDA такие же, как и для PDA, за исключением того, что «и » теперь являются строками, а не символами. ${\displaystyle a_{i+1}}$ ${\displaystyle b_{i+1}}$

GPDA и PDA эквивалентны в том смысле, что если язык распознается PDA, он также распознается GPDA, и наоборот.

Можно сформулировать аналитическое доказательство эквивалентности GPDA и PDA, используя следующую симуляцию:

Пусть будет переход GPDA ${\displaystyle \delta (q_{1},w,x_{1}x_{2}\cdot x_{m})\longrightarrow (q_{2},y_{1}y_{2}...y_{n})}$

где . ${\displaystyle q_{1},q_{2}\in Q,w\in \Sigma _{\epsilon },x_{1},x_{2},\ldots ,x_{m}\in \Gamma ^{*},m\geq 0,y_{1},y_{2},\ldots ,y_{n}\in \Gamma ^{*},n\geq 0}$

Постройте следующие переходы для КПК:

${\displaystyle {\begin{array}{lcl}\delta '(q_{1},w,x_{1})&\longrightarrow &(p_{1},\epsilon )\\\delta '(p_{1},\epsilon ,x_{2})&\longrightarrow &(p_{2},\epsilon )\\&\vdots &\\\delta '(p_{m-1},\epsilon ,x_{m})&\longrightarrow &(p_{m},\epsilon )\\\delta '(p_{m},\epsilon ,\epsilon )&\longrightarrow &(p_{m+1},y_{n})\\\delta '(p_{m+1},\epsilon ,\epsilon )&\longrightarrow &(p_{m+2},y_{n-1})\\&\vdots &\\\delta '(p_{m+n-1},\epsilon ,\epsilon )&\longrightarrow &(q_{2},y_{1}).\end{array}}}$

Стек автоматов

В качестве обобщения стековых автоматов Гинзбург, Грейбах и Харрисон (1967) исследовали стековые автоматы , которые могут дополнительно переходить влево или вправо во входной строке (окруженные специальными символами-маркерами конца для предотвращения выскальзывания) и переходить вверх или вниз по стеку в режиме только для чтения. ^{[6] [7]} Стековый автомат называется нестирающим, если он никогда не выталкивается из стека. Класс языков, принимаемых недетерминированными, нестирающими стековыми автоматами, — это NSPACE ( n ² ), который является надмножеством контекстно -зависимых языков . ^[1] Класс языков, принимаемых детерминированными, нестирающими стековыми автоматами, — это DSPACE ( n ⋅log( n )). ^[1]

Автоматы с чередующимся нажатием

Автомат с чередующимся магазином (APDA) — это магазин с набором состояний

• ${\displaystyle Q=Q_{\exists }\cup Q_{\forall }}$где . ${\displaystyle Q_{\exists }\cap Q_{\forall }=\emptyset }$

Состояния в и называются экзистенциальными соответственно универсальными . В экзистенциальном состоянии APDA недетерминированно выбирает следующее состояние и принимает, если хотя бы одно из результирующих вычислений принимает. В универсальном состоянии APDA переходит ко всем следующим состояниям и принимает, если все результирующие вычисления принимают. ${\displaystyle Q_{\exists }}$ ${\displaystyle Q_{\forall }}$

Модель была введена Чандрой , Козеном и Стокмейером . ^[8] Ладнер , Липтон и Стокмейер ^[9] доказали, что эта модель эквивалентна EXPTIME , т.е. язык принимается некоторой APDA тогда и только тогда , когда он может быть решен с помощью алгоритма с экспоненциальным временем.

Айзиковиц и Камински ^[10] представили синхронизированные чередующиеся автоматы с магазинной памятью (SAPDA), которые эквивалентны конъюнктивным грамматикам так же, как недетерминированные PDA эквивалентны контекстно-свободным грамматикам.

Смотрите также

• Контекстно-свободная грамматика
• Счетчик автоматов
• Конечный автомат
• Автомат очереди
• Машина для укладки штабеля

Примечания

1. Набор палиндромов битов четной длины не может быть распознан детерминированным КПК, но является контекстно-свободным языком с грамматикой S → ε | 0 S 0 | 1 S 1. ^[4]
2. Линейные ограниченные автоматы являются акцепторами для класса контекстно-зависимых языков, ^{[2] : 225} который является собственным суперклассом контекстно-свободных языков и собственным подклассом языков, распознаваемых по Тьюрингу (т.е. рекурсивно перечислимых ). ^{[2] : 228}

Ссылки

1. Джон Э. Хопкрофт; Джеффри Д. Ульман (1967). «Автоматы без стирания стека». Журнал компьютерных и системных наук . 1 (2): 166–186. doi : 10.1016/s0022-0000(67)80013-8 .
2. Джон Э. Хопкрофт и Джеффри Д. Ульман (1979). Введение в теорию автоматов, языки и вычисления . Чтение/MA: Addison-Wesley. ISBN 0-201-02988-X.
3. "Pushdown Automata". www.cs.odu.edu . Получено 2024-04-07 .
4. Джон Э. Хопкрофт; Раджив Мотвани; Джеффри Д. Ульман (2003). Введение в теорию автоматов, языки и вычисления . Эддисон Уэсли.Здесь: Раздел 6.4.3, стр.249
5. Хольцер, Маркус; Кутриб, Мартин (2019). «Нерекурсивные компромиссы есть «почти везде»". Вычисления с предвидением и промышленностью . 11558 : 25–36. doi :10.1007/978-3-030-22996-2_3.Это следует из цитируемого [22, Предложение 7] и изложенного наблюдения, что любой детерминированный магазинный автомат может быть преобразован в эквивалентный конечный автомат ^{[ уточнить ]} не более чем дважды экспоненциального размера.
6. Сеймур Гинзбург, Шейла А. Грейбах и Майкл А. Харрисон (1967). «Стековые автоматы и компиляция». J. ACM . 14 (1): 172–201. doi : 10.1145/321371.321385 .
7. Сеймур Гинзбург, Шейла А. Грейбах и Майкл А. Харрисон (1967). «Односторонние стековые автоматы». J. ACM . 14 (2): 389–418. doi : 10.1145/321386.321403 .
8. Чандра, Ашок К.; Козен, Декстер К.; Стокмейер, Ларри Дж. (1981). «Alternation». Журнал ACM . 28 (1): 114–133. doi : 10.1145/322234.322243 . ISSN  0004-5411.
9. Ladner, Richard E.; Lipton, Richard J.; Stockmeyer, Larry J. (1984). «Alternating Pushdown and Stack Automata». SIAM Journal on Computing . 13 (1): 135–155. doi :10.1137/0213010. ISSN  0097-5397.
10. Айзиковиц, Тамар; Камински, Майкл (2011). "LR(0) Конъюнктивные грамматики и детерминированные синхронизированные чередующиеся магазинные автоматы". Информатика – Теория и приложения . Конспект лекций по информатике. Том 6651. С. 345–358. doi :10.1007/978-3-642-20712-9_27. ISBN 978-3-642-20711-2. ISSN  0302-9743.

• Майкл Сипсер (1997). Введение в теорию вычислений . PWS Publishing. ISBN 0-534-94728-X.Раздел 2.2: Автоматы с толкающим механизмом, стр. 101–114.
• Жан-Мишель Отебер, Жан Берстель, Люк Боассон, Контекстно-свободные языки и автоматы с выдвижной книгой, в: Г. Розенберг, А. Саломаа (ред.), Справочник по формальным языкам, т. 1, Springer-Verlag, 1997, 111–174.

Внешние ссылки

• JFLAP, симулятор для нескольких типов автоматов, включая недетерминированные автоматы с магазинной стойкой
• CoAn — еще один симулятор для нескольких типов машин, включая недетерминированные автоматы с магазинной памятью (C++, Windows, Linux, MacOS)