Ментальный расчет

Арифметические вычисления с использованием только человеческого мозга

Ментальный счет уже давно стал составной частью математического образования.

Ментальный расчет состоит из арифметических вычислений, в которых используется только человеческий мозг , без помощи каких-либо расходных материалов (например, карандаша и бумаги) или таких устройств, как калькулятор . Люди могут использовать мысленный расчет, когда вычислительные инструменты недоступны, когда он быстрее, чем другие средства расчета (например, традиционные методы образовательных учреждений) или даже в конкурентном контексте . Ментальный расчет часто предполагает использование конкретных методов, разработанных для конкретных типов задач. Людей с необычайно высокими способностями к умственным вычислениям называют мысленными калькуляторами или молниеносными калькуляторами .

Многие из этих методов используют десятичную систему счисления или полагаются на нее. Обычно выбор системы счисления определяет, какой метод или методы использовать.

Методы и техники

Выбрасывание девяток

После применения арифметической операции к двум операндам и получения результата для повышения уверенности в правильности результата можно использовать следующую процедуру:

1. Суммируйте цифры первого операнда; любые девятки (или наборы цифр, которые в сумме дают 9) можно считать 0.
2. Если полученная сумма имеет две или более цифр, просуммируйте эти цифры, как на первом этапе; повторяйте этот шаг до тех пор, пока полученная сумма не будет иметь только одну цифру.
3. Повторите шаги первый и второй со вторым операндом. На этом этапе есть два однозначных числа: первое, полученное из первого операнда, и второе, полученное из второго операнда. ^[а]
4. Примените первоначально указанную операцию к двум сжатым операндам, а затем примените процедуру суммирования цифр к результату операции.
5. Просуммируйте цифры результата, которые были изначально получены при исходном расчете.
6. Если результат шага 4 не равен результату шага 5, то исходный ответ неверен. Если два результата совпадают, то исходный ответ может быть правильным, хотя это и не гарантируется.

Пример

• Предположим, что вычисление 6338 × 79, выполненное вручную, дало результат 500702:

1. Сложите цифры 6338: (6 + 3 = 9, считайте это за 0) + 3 + 8 = 11.
2. Повторяйте по мере необходимости: 1 + 1 = 2.
3. Суммируем цифры 79: 7 + (9 считается 0) = 7.
4. Выполните исходную операцию над сжатыми операндами и просуммируйте цифры: 2 × 7 = 14; 1 + 4 = 5
5. Сложите цифры 500702: 5 + 0 + 0 + (7 + 0 + 2 = 9, что считается 0) = 5.
6. 5 = 5, так что есть большая вероятность, что предсказание о том, что 6338 × 79 равно 500702, окажется верным.

Эту же процедуру можно использовать для нескольких операций, повторяя шаги 1 и 2 для каждой операции.

Факторы

При умножении полезно помнить, что множители операндов остаются. Например, сказать, что 14×15 равно 201, было бы неразумно. Поскольку 15 кратно 5, то и произведение должно быть кратным. Аналогично, 14 кратно 2, поэтому произведение должно быть четным. Кроме того, любое число, кратное 5 и 2, обязательно кратно 10, а в десятичной системе оканчивается на 0. Правильный ответ — 210. Это число кратно 10, 7 (другой простой множитель 14) и 3 (другой простой делитель 15).

Вычисление разностей: a − b

Прямой расчет

Когда все цифры b меньше соответствующих цифр a , вычисление может выполняться по цифрам. Например, оцените 872 − 41, просто вычитая 1 из 2 в разряде единиц и 4 из 7 в разряде десятков: 831.

Косвенный расчет

Если описанная выше ситуация неприменима, существует другой метод, известный как косвенный расчет.

Метод прогнозного заимствования

Этот метод можно использовать для вычитания чисел слева направо, и если все, что требуется, — это прочитать результат вслух, он требует мало памяти пользователя даже для вычитания чисел произвольного размера.

Обрабатывается одно место за раз, слева направо.

Пример: 4075 − 1844 г. ------Тысячи: 4 − 1 = 3, посмотрите направо, 075 < 844, нужно одолжить. 3 − 1 = 2, скажем «Две тысячи». Вы выполняете 3–1, а не 4–1, потому что столбец справа собираюсь занять тысячу мест.Сотни: 0–8 = отрицательные числа здесь не допускаются. Это место можно увеличить, используя цифру один, заимствованную из столбец слева. Поэтому: 10 − 8 = 2. Это 10, а не 0, потому что единица заимствована у Тысячи место. 75 > 44, так что не надо брать взаймы, скажи "двести"Десятки: 7–4 = 3, 5 > 4, поэтому 5–4 = 1.

Следовательно, результат равен 2231.

Расчет продуктов: а × б

Многие из этих методов работают благодаря распределительному свойству .

Умножение любых двух чисел путем присоединения, вычитания и маршрутизации.

Открытый Артемом Чепрасовым метод умножения позволяет пользователю за три шага быстро умножать числа любого размера друг на друга тремя уникальными способами. ^{[1] [2]}

Во-первых, метод позволяет пользователю присоединять числа друг к другу, а не складывать или вычитать их на промежуточных этапах, чтобы ускорить скорость умножения. Например, вместо сложения или вычитания промежуточных результатов, таких как 357 и 84, пользователь может просто соединить числа (35784), чтобы упростить и ускорить задачу умножения. Соединение чисел друг с другом помогает обойти ненужные шаги, встречающиеся в традиционных методах умножения.

Во-вторых, этот метод использует отрицательные числа по мере необходимости, даже при умножении двух положительных целых чисел, чтобы ускорить скорость умножения за счет вычитания. Это означает, что два положительных целых числа можно перемножить, чтобы получить отрицательные промежуточные шаги, но в конечном итоге получить правильный положительный ответ. Эти отрицательные числа фактически автоматически выводятся из самих шагов умножения и, таким образом, уникальны для конкретной задачи. Опять же, такие негативные промежуточные шаги предназначены для ускорения мысленных вычислений.

Наконец, еще одним уникальным аспектом использования этого метода является то, что пользователь может выбрать один из нескольких различных «путей умножения» для конкретной задачи умножения, основываясь на своих субъективных предпочтениях или сильных и слабых сторонах конкретных целых чисел.

Несмотря на одинаковые начальные целые числа, разные способы умножения дают разные промежуточные числа, которые автоматически получаются для пользователя по мере их умножения. Некоторые из этих посредников могут быть проще, чем другие (например, некоторые пользователи могут найти маршрут, в котором используется отрицательная цифра 7, в то время как другой маршрут использует цифру 5 или 0, с которыми большинству людей обычно легче работать в уме, но не во всех случаях). ).

Если один «маршрут» кажется одному ученику более сложным по сравнению с другим маршрутом и его промежуточными числами, этот ученик может просто выбрать для себя другой, более простой путь умножения, даже если это та же исходная задача.

Формула «Конец пяти»

Для любой задачи умножения 2 цифр на 2 цифры, если оба числа оканчиваются на пять, можно использовать следующий алгоритм для их быстрого умножения: ^[1]

${\displaystyle \mathrm {Ex} :35\times 75}$

В качестве предварительного шага просто округлите меньшее число в меньшую сторону и большее в большую сторону до ближайшего числа, кратного десяти. В этом случае:

${\displaystyle 35-5=30=X}$

${\displaystyle 75+5=80=Y}$

Алгоритм звучит следующим образом:

${\displaystyle (X\times Y)+50(t_{1}-t_{2})+25}$

Где t ₁ — это единица десятков исходного большего числа (75), а t ₂ — это единица десятков исходного меньшего числа (35).

${\displaystyle =30\times 80+50(7-3)+25=2625}$

Автор также описывает еще один аналогичный алгоритм, если вместо этого нужно округлить исходное большее число в меньшую сторону, а исходное меньшее — в большую сторону.

Формула «заемщика»

Если два числа равноудалены от ближайшего кратного 100, то для нахождения произведения можно использовать простой алгоритм. ^[1]

В качестве простого примера:

${\displaystyle 33\times 67}$

Оба числа равноудалены (33) от ближайшего числа, кратного 100 (0 и 100 соответственно).

В качестве предварительного шага просто округлите меньшее число в меньшую сторону и большее в большую сторону до ближайшего числа, кратного десяти. В этом случае:

${\displaystyle 33-3=30=X}$

${\displaystyle 67+3=70=Y}$

Алгоритм звучит следующим образом:

${\displaystyle (X\times Y)+u_{1}\times u_{2}+u_{2}(T_{1}-T_{2})}$

Где u ₁ — это цифра единиц исходного большего числа (67), а u ₂ — цифра единиц исходного меньшего числа (33). T ₁ — это цифра десятков исходного большего числа, а T ₂ — это цифра десятков исходного большего числа, умноженная на соответствующую степень (в данном случае на 10 для цифры десятков).

И так:

${\displaystyle (30\times 70)+7\times 3+3(60-30)=2100+21+90=2211}$

Умножение любых двузначных чисел

Чтобы легко перемножить любые двузначные числа, существует простой алгоритм, следующий (где a — цифра десятков первого числа, b — цифра единиц первого числа, c — цифра десятков второго числа, а d — цифра десятков второго числа). одна цифра второго числа):

${\displaystyle (10a+b)\cdot (10c+d)}$

${\displaystyle =100(a\cdot c)+10(b\cdot c)+10(a\cdot d)+b\cdot d}$

Например,

${\displaystyle 23\cdot 47=100(2\cdot 4)+10(3\cdot 4)+10(2\cdot 7)+3\cdot 7}$

 800 +120 +140 + 21----- 1081

Обратите внимание, что это то же самое, что и обычная сумма частичных произведений, просто сформулированная кратко. Чтобы свести к минимуму количество элементов, сохраняемых в памяти, может быть удобно сначала выполнить сумму произведения «перекрестного» умножения, а затем добавить два других элемента:

${\displaystyle (a\cdot d+b\cdot c)\cdot 10}$

${\displaystyle {}+b\cdot d}$[из которых только цифра десятков будет мешать первому члену]

${\displaystyle {}+a\cdot c\cdot 100}$

то есть в этом примере

(12+14)=26, 26×10=260,

к чему легко добавить 21:281 а потом 800:1081

Для этого проще всего запомнить FOIL . F означает первый, O означает внешний, I означает внутренний и L означает последний. Например:

${\displaystyle 75\cdot 23}$

и

${\displaystyle ab\cdot cd}$

где 7 это а , 5 это б , 2 это в и 3 это d .

Учитывать

${\displaystyle a\cdot c\cdot 100+(a\cdot d+b\cdot c)\cdot 10+b\cdot d}$

это выражение аналогично любому числу по основанию 10 с сотнями, десятками и единицами. FOIL также можно рассматривать как число, где F — сотни, OI — десятки, а L — единицы.

${\displaystyle a\cdot c}$— произведение первой цифры каждого из двух чисел; Ф.

${\displaystyle (a\cdot d+b\cdot c)}$представляет собой сложение произведения внешних цифр и внутренних цифр; Ой.

${\displaystyle b\cdot d}$является произведением последней цифры каждого из двух чисел; Л.

Умножение на 2 или другие небольшие числа

Если одно умножаемое число достаточно мало, чтобы его можно было легко умножить на любую однозначную цифру, произведение можно легко вычислить по цифрам справа налево. Это особенно легко сделать при умножении на 2, поскольку цифра переноса не может быть больше 1.

Например, чтобы вычислить 2 × 167: 2 × 7 = 14, поэтому последняя цифра — 4 , с переносимой 1 и добавлением к 2 × 6 = 12, чтобы получить 13, поэтому следующая цифра — 3 с переносимой 1 и добавлено к 2×1=2, чтобы получить 3 . Таким образом, произведение равно 334.

Умножение на 5

Чтобы умножить число на 5,

1. Сначала умножьте это число на 10, затем разделите его на 2. Эти два шага взаимозаменяемы, т.е. можно разделить число вдвое, а затем умножить его.

Следующий алгоритм — быстрый способ получить этот результат:

2. Добавьте ноль справа от нужного числа. (А.) 3. Далее, начиная с крайней левой цифры, разделите на 2 (Б.) и прибавьте каждый результат в соответствующем порядке, чтобы образовать новое число; (ответы дробей следует округлить до ближайшего целого числа).

ПРИМЕР: Умножьте 176 на 5. А. Добавьте ноль к 176, чтобы получить 1760. B. Разделите на 2, начиная слева. 1. Разделите 1 на 2, чтобы получить 0,5, округленное до нуля. 2. Разделите 7 на 2 и получите 3,5, округлив до 3. 3. Разделите 6 на 2, чтобы получить 3. Ноль, разделенный на два, — это просто ноль.

Полученное число — 0330. (Это не окончательный ответ, а первое приближение, которое будет скорректировано на следующем этапе:)

 C. Добавьте 5 к числу, которое следует за любой отдельной цифрой. в этом новом числе, которое было нечетным до деления на два;

ПРИМЕР: 176 (НА ПЕРВОМ, ВТОРОМ, ТРЕТЬЕМ МЕСТАХ):

 1. ПЕРВОЕ место – 1, что нечетно. ДОБАВЬТЕ 5 к цифре после первое место в новом номере (0330) — 3; 3+5=8.  2.Число на втором месте 176,7 тоже нечетное.  соответствующее число (0 8 3 0) также увеличивается на 5; 3+5=8. 3.Числа на третьем месте в числе 176,6 четная, следовательно последнее число, ноль, в ответе не меняется. Что окончательный ответ: 0880. Крайний левый ноль можно опустить, оставив 880. Итак, 176 умножить на 5 будет 880.

ПРИМЕР: Умножьте 288 на 5.

А. Разделите 288 на 2. Можно разделить каждую цифру по отдельности, чтобы получить 144. (Делить меньшее число проще.)

Б. Умножьте на 10. Добавьте ноль, чтобы получить результат 1440.

Умножение на 9

Поскольку 9 = 10 − 1, чтобы умножить число на девять, умножьте его на 10, а затем вычтите исходное число из результата. Например, 9×27 = 270–27 = 243.

Этот метод можно настроить для умножения на восемь вместо девяти, удвоив вычитаемое число; 8×27 = 270 – (2×27) = 270 – 54 = 216.

Аналогичным образом, используя сложение вместо вычитания, те же методы можно использовать для умножения на 11 и 12 соответственно (хотя существуют и более простые методы умножения на 11).

Использование рук: 1–10, умноженное на 9.

Считаем 9×8 пальцами.

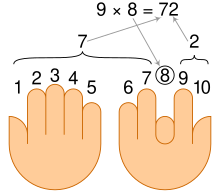
Чтобы использовать этот метод, необходимо положить руки перед собой ладонями к себе. Присвойте левому большому пальцу цифру 1, левому указательному значению — 2, и так далее, пока правый большой палец не станет равным десяти. Каждый "|" символизирует поднятый палец, а «-» означает согнутый палец.

1 2 3 4 5 6 7 8 9 10| | | | | | | | | |левая рука правая рука

Согните вниз палец, обозначающий число, которое нужно умножить на девять.

Пример: 6 × 9 будет

| | | | | − | | | |

Правый мизинец опущен вниз. Возьмите количество пальцев, все еще поднятых слева от согнутого пальца, и прибавьте его к количеству пальцев справа.

Пример: пять пальцев слева от правого мизинца и четыре справа от правого мизинца. Итак, 6 × 9 = 54.

 5 4| | | | | − | | | |

Умножение на 10 (и степени десяти)

Чтобы умножить целое число на 10, просто добавьте дополнительный 0 в конец числа. Чтобы умножить нецелое число на 10, переместите десятичную точку на одну цифру вправо.

Обычно для десятичной системы умножения на 10 ⁿ (где n — целое число) переместите десятичную точку на n цифр вправо. Если n отрицательно, переместите десятичную дробь | п | цифры слева.

Умножение на 11

Для однозначных чисел просто умножьте число на десятки, например: 1 × 11 = 11, 2 × 11 = 22, вплоть до 9 × 11 = 99.

Произведение любого большего ненулевого целого числа можно найти путем сложения каждой его цифры справа налево, по две за раз.

Сначала возьмите единицу и скопируйте ее во временный результат. Затем, начиная с единицы множителя, прибавьте каждую цифру к цифре слева от нее. Затем каждая сумма добавляется слева от результата перед всеми остальными. Если сумма числа равна 10 или больше, возьмите цифру десятков, которая всегда будет 1, и перенесите ее в следующее сложение. Наконец, скопируйте самую левую (наибольшую) цифру множителя в начало результата, прибавив при необходимости переносимую 1, чтобы получить конечный продукт.

В случае отрицательного числа 11 множитель или оба примените знак к конечному продукту, как при обычном умножении двух чисел.

Пошаговый пример 759×11:

1. Единичная цифра множителя, 9, копируется во временный результат.
   • результат: 9
2. Добавьте 5 + 9 = 14, чтобы 4 оказалось слева от результата, и сохраните 1.
   • результат: 49
3. Аналогичным образом сложите 7 + 5 = 12, затем прибавьте перенесенную 1, чтобы получить 13. Поместите 3 к результату и перенесите 1.
   • результат: 349
4. Добавьте перенесенную 1 к старшей цифре множителя, 7 + 1 = 8, и скопируйте результат, чтобы закончить.
   • Конечный продукт 759×11:8349

Дальнейшие примеры:

• −54 × −11 = 5 5+4(9) 4 = 594
• 999 × 11 = 9+1(10) 9+9+1(9) 9+9(8) 9 = 10989
  • Обратите внимание на обработку 9+1 как самой старшей цифры.
• −3478 × 11 = 3 3+4+1(8) 4+7+1(2) 7+8(5) 8 = −38258
• 62473 × 11 = 6 6+2(8) 2+4+1(7) 4+7+1(2) 7+3(0) 3 = 687203

Другой метод — просто умножить число на 10 и прибавить исходное число к результату.

Например:

17 × 11

 17 × 10 = 170

170 + 17 = 187

17 × 11 = 187

Последний простой способ:

Если у кого-то есть двузначное число, возьмите его, сложите два числа и поместите эту сумму в середину, и вы получите ответ.

Например: 24 x 11 = 264, потому что 2 + 4 = 6, а цифра 6 находится между 2 и 4.

Второй пример: 87 x 11 = 957, потому что 8 + 7 = 15, поэтому 5 стоит между 8 и 7, а 1 переносится в 8. Таким образом, по сути это 857 + 100 = 957.

Или, если 43 x 11 равно первым 4+3=7 (для десятков). Тогда 4 — для сотен, а 3 — для десятков. И ответ 473

Умножение двух двузначных чисел от 11 до 19.

Чтобы легко умножить двухзначные числа от 11 до 19, можно воспользоваться следующим простым алгоритмом (где a — цифра единиц первого числа, а b — цифра единиц второго числа):

(10+а)×(10+б)100 + 10×(a+b) + а×bкоторый можно представить как три добавляемые части:1хх ууунапример:17×161 = 10013 (7+6) = 10×(а+б) 42 (7×6) = а×б272 (всего)

Используя руки: 6–10, умноженное на другое число 6–10.

Вычисление 9×8 и 7×6

Этот прием позволяет умножить число от 6 до 10 на другое число от 6 до 10.

Назначьте мизинцу 6, безымянному пальцу 7, среднему пальцу 8, указательному 9 и большому пальцу 10. Коснитесь двух нужных цифр вместе. Точка соприкосновения и нижняя часть считаются «нижней» частью, а все, что находится над двумя соприкасающимися пальцами, является частью «верхней» части. Ответ формируется путем прибавления десятикратного общего количества «нижних» пальцев к произведению количества «верхних» пальцев левой и правой руки.

Например, 9 × 6 будет выглядеть так: левый указательный палец касается правого мизинца:

 =10== :большой палец правой руки (сверху) ==9== :указательный палец правой руки (сверху) ==8== :средний палец правой руки (сверху) большой палец левой руки: =10== ==7== :безымянный палец правой руки (сверху)  левый указательный палец: --9---><---6-- :правый мизинец (НИЗ) средний палец левой руки: --8-- (НИЖНИЙ) левый безымянный палец: --7-- (НИЖНЯЯ)левый мизинец: --6-- (ВНИЗУ)

В этом примере имеется 5 «нижних» пальцев (указательный, средний, безымянный и мизинец левой руки, а также правый мизинец), 1 левый «верхний» палец (большой палец левой руки) и 4 правых «верхних» пальца. (правый большой палец, указательный палец, средний палец и безымянный палец). Таким образом, вычисление происходит следующим образом: 9 × 6 = (10 × 5) + (1 × 4) = 54.

Рассмотрим другой пример, 8 × 7:

 =10== :большой палец правой руки (сверху) большой палец левой руки: =10== ==9== :указательный палец правой руки (сверху) указательный палец левой руки: ==9== ==8== :средний палец правой руки (сверху)средний палец левой руки: --8---><---7-- :безымянный палец правой руки (НИЖНЯЯ) левый безымянный палец: --7-- --6-- :правый мизинец (НИЖНИЙ)левый мизинец: --6-- (ВНИЗУ)

Пять нижних пальцев составляют 5 десятков, или 50. Два верхних левых пальца и три верхних правых пальца дают произведение 6. Их суммирование дает ответ: 56.

Другой пример, на этот раз с использованием 6 × 8:

--8---><---6-- --7-- --6--

Четыре десятка (внизу) плюс два раза по четыре (вверху) дают 40 + 2×4 = 48.

Вот как это работает: каждый палец представляет число от 6 до 10. Когда соединяются пальцы, представляющие x и y , на левой руке будет 10 - x "верхних" пальцев и x -5 "нижних" пальцев; на правой руке будет 10- y «верхних» пальцев и y -5 «нижних» пальцев.

Позволять

${\displaystyle \,t_{L}=10-x\,}$(количество «верхних» пальцев на левой руке)

${\displaystyle \,t_{R}=10-y\,}$(количество «верхних» пальцев на правой руке)

${\displaystyle \,b_{L}=x-5\,}$(количество «нижних» пальцев на левой руке)

${\displaystyle \,b_{R}=y-5\,}$(количество «нижних» пальцев на правой руке)

Затем, следуя приведенным выше инструкциям, вы получите

${\displaystyle \,10(b_{L}+b_{R})+t_{L}t_{R}}$

${\displaystyle \,=10[(x-5)+(y-5)]+(10-x)(10-y)}$

${\displaystyle \,=10(x+y-10)+(100-10x-10y+xy)}$

${\displaystyle \,=[10(x+y)-100]+[100-10(x+y)+xy]}$

${\displaystyle \,=[10(x+y)-10(x+y)]+[100-100]+xy}$

${\displaystyle \,=xy}$

какой продукт нужен.

Умножение двух чисел, близких к 100 и ниже

Этот метод позволяет легко умножать числа, близкие к 100 и ниже. (90-99) ^[3] Переменными будут два числа, которые умножаются на одно.

Произведение двух переменных в диапазоне от 90 до 99 даст 4-значное число. Первым делом нужно найти цифры единиц и цифр десятков.

Вычтите обе переменные из 100, что даст 2 однозначных числа. Произведение двух однозначных чисел будет двумя последними цифрами конечного продукта.

Затем вычтите одну из двух переменных из 100. Затем вычтите разницу из другой переменной. Эта разница будет первыми двумя цифрами конечного продукта, а полученное 4-значное число будет конечным продуктом.

Пример:

 95 х 97 ----Последние две цифры: 100-95=5 (из 100 вычесть первое число) 100-97=3 (вычесть второе число из 100) 5*3=15 (перемножить две разницы) Конечный продукт — yx15Первые две цифры: 100-95=5 (вычтите первое число уравнения из 100) 97-5=92 (Вычтите этот ответ из второго числа уравнения) Теперь разница будет заключаться в первых двух цифрах.  Конечный продукт — 9215.Альтернатива для первых двух цифр 5+3=8 (сложите две одиночные цифры, полученные при вычислении «последних двух цифр» на предыдущем шаге) 100-8=92 (Вычтите этот ответ из 100) Теперь разница будет заключаться в первых двух цифрах.  Конечный продукт — 9215.

Использование квадратных чисел

Произведения небольших чисел можно вычислить, используя квадраты целых чисел; например, чтобы вычислить 13 × 17, можно заметить, что 15 — это среднее значение двух факторов, и думать об этом как (15 — 2) × (15 + 2), т. е. 15 ²  — 2 ² . Зная, что 15 ² равно 225, а 2 ² равно 4, простое вычитание показывает, что 225 − 4 = 221, что и есть искомое произведение.

Этот метод требует знания наизусть определенного количества квадратов:

Возведение чисел в квадрат

Возможно, будет полезно знать, что разница между двумя последовательными квадратными числами равна сумме их соответствующих квадратных корней. Следовательно, если кто-то знает, что 12 × 12 = 144, и желает знать 13 × 13, вычислите 144 + 12 + 13 = 169.

Это потому, что ( x  + 1) ²  −  x ² = x ²  + 2 x  + 1 −  x ² = x  + ( x  + 1)

Икс ² = ( Икс  - 1) ² + (2 Икс  - 1)

Возведение в квадрат любого числа

Возьмите данное число, прибавьте и вычтите к нему определенное значение, которое облегчит умножение. Например:

492 ²

492 близко к 500, на которое легко умножить. Сложите и вычтите 8 (разницу между 500 и 492), чтобы получить

492 -> 484, 500

Умножьте эти числа, чтобы получить 242 000 (это можно эффективно сделать, разделив 484 на 2 = 242 и умножив на 1000). Наконец, добавьте к результату разность (8) в квадрате (8 ^{2 = 64):}

492 ² = 242 064

Доказательство следующее:

${\displaystyle n^{2}=n^{2}}$

${\displaystyle n^{2}=(n^{2}-a^{2})+a^{2}}$

${\displaystyle n^{2}=(n^{2}-an+an-a^{2})+a^{2}}$

${\displaystyle n^{2}=(n-a)(n+a)+a^{2}}$

Возведение в квадрат любого двузначного целого числа

Этот метод требует запоминания квадратов однозначных чисел от 1 до 9.

Квадрат mn , где mn представляет собой двузначное целое число, может быть рассчитан как

10 × м ( мн + п ) + п ²

Это означает, что квадрат mn можно найти, добавив n к mn , умножив на m , добавив 0 в конец и, наконец, добавив квадрат n .

Например, 23 ² :

23 ²

= 10 × 2(23 + 3) + 3 ²

= 10 × 2(26) + 9

= 520 + 9

= 529

Итак, 23 ² = 529.

Возведение в квадрат числа, оканчивающегося на 5

1. Возьмите цифры, которые предшествуют пяти: abc5 , где a, b и c — цифры.
2. Умножьте это число само на себя плюс один: abc ( abc + 1)
3. Возьмите приведенный выше результат и присоедините 25 к концу
   • Пример: 85 × 85
     1. 8
     2. 8 × 9 = 72
     3. Итак, 85 ² = 7,225
   • Пример: 125 ²
     1. 12
     2. 12 × 13 = 156
     3. Итак, 125 ² = 15 625
   • Математическое объяснение

Квадратирование чисел очень близко к 50

Предположим, нужно возвести в квадрат число n около 50.

Число можно выразить как n  = 50 −  a , поэтому его квадрат равен (50− a ) ² = 50 ² − 100 a + a ² . Известно, что 50 ^{2 равно 2500. Итак ,} из 2500 вычитают 100 a , а затем прибавляют 2 .

Например, скажем, кто-то хочет возвести в квадрат 48, что равно 50 - 2. Из 2500 вычитают 200, прибавляют 4 и получают n ² = 2304. Для чисел больше 50 ( n  = 50 +  a ) вместо этого прибавляйте 100× a. вычитания его.

Возведение в квадрат целого числа от 26 до 74

Этот метод требует запоминания квадратов от 1 до 24.

Квадрат n (легче всего вычисляется, когда n находится в диапазоне от 26 до 74 включительно) равен

(50 - п ) ² + 100( п - 25)

Другими словами, квадрат числа — это квадрат его разности от пятидесяти, прибавленной к стократной разности числа и двадцати пяти. Например, в квадрат 62:

(−12) ² + [(62–25) × 100]

= 144 + 3700

= 3844

Возведение в квадрат целого числа, близкого к 100 (например, от 76 до 124)

Этот метод требует запоминания квадратов от 1 до a , где a — абсолютная разница между n и 100. Например, учащиеся, запомнившие квадраты от 1 до 24, могут применить этот метод к любому целому числу от 76 до 124.

Квадрат n (т.е. 100 ± a ) равен

100(100 ± 2 а ) + а ²

Другими словами, квадрат числа — это квадрат его разности со 100, прибавленной к произведению ста и разности ста и произведению двух и разности ста и числа. Например, в квадрат 93:

100(100 - 2(7)) + 7 ²

= 100 × 86 + 49

= 8600 + 49

= 8,649

Другой способ взглянуть на это будет так:

93 ² = ? (составляет −7 из 100)

93 − 7 = 86 (это первые две цифры)

(−7) ² = 49 (это вторые две цифры)

93 ² = 8649

Другой пример:

82 2 = ? (составляет −18 из 100) 82 − 18 = 64 (вычесть. Первые цифры.) (-18) 2 = 324 (вторая пара цифр. Нужно будет иметь при себе 3.) 82 2 = 6724

Возведение в квадрат любого целого числа, близкого к 10 ⁿ (например, от 976 до 1024, от 9976 до 10024 и т. д.)

Этот метод является прямым расширением приведенного выше объяснения возведения в квадрат целого числа, близкого к 100.

1012 2 = ? (1012 — это +12 от 1000) (+12) 2 = 144 ( n конечных цифр) 1012 + 12 = 1024 (начальные цифры) 1012 2 = 1024144

9997 2 = ? (9997 — это -3 от 10 000) (-3) 2 = 0009 ( n конечных цифр) 9997 – 3 = 9994 (начальные цифры) 9997 2 = 99940009

Возведение в квадрат любого целого числа, близкого к m × 10 ⁿ (например, от 276 до 324, от 4976 до 5024, от 79976 до 80024)

Этот метод является прямым расширением объяснения, данного выше для целых чисел около 10 ⁿ .

407 2 = ? (407 — это +7 от 400) (+7) 2 = 49 ( n конечных цифр) 407 + 7 = 414 414 × 4 = 1656 (начальные цифры; обратите внимание, что умножение на m не требовалось для целых чисел от 76 до 124, поскольку их m = 1) 407 2 = 165649

79991 2 = ? (79991 это -9 от 80000) (-9) 2 = 0081 ( n конечных цифр) 79991 - 9 79982 × 8 = 639856 (начальные цифры) 79991 2 = 6398560081

Поиск корней

Аппроксимация квадратных корней

Простой способ получить квадратный корень числа — использовать следующее уравнение:

${\displaystyle {\text{root }}\simeq {\text{ known square root}}-{\frac {{\text{known square}}-{\text{unknown square}}}{2\times {\text{known square root}}}}\,}$

Чем ближе известный квадрат к неизвестному, тем точнее приближение. Например, чтобы оценить квадратный корень из 15, можно начать с знания, что ближайший идеальный квадрат равен 16 (4 ² ).

${\displaystyle {\begin{aligned}{\text{root}}&\simeq 4-{\frac {16-15}{2\times 4}}\\&\simeq 4-0.125\\&\simeq 3.875\\\end{aligned}}\,\!}$

Таким образом, предполагаемый квадратный корень из 15 равен 3,875. Фактический квадратный корень из 15 равен 3,872983. Следует отметить, что независимо от исходного предположения, предполагаемый ответ всегда будет больше фактического ответа из-за неравенства средних арифметических и геометрических . Таким образом, следует попробовать округлить предполагаемый ответ в меньшую сторону.

Заметим, что если n ² — ближайший к искомому квадрату x идеальный квадрат , а d = x — n ² — их разность, то удобнее выразить это приближение в виде смешанной дроби как . Таким образом, в предыдущем примере квадратный корень из 15 равен. Другой пример: квадратный корень из 41 равен фактическому значению 6,4031... ${\displaystyle n{\tfrac {d}{2n}}}$ ${\displaystyle 4{\tfrac {-1}{8}}.}$ ${\displaystyle 6{\tfrac {5}{12}}=6.416}$

Можно упростить мысленные вычисления, заметив, что этот метод эквивалентен среднему известному квадрату и неизвестному квадрату, разделенному на известный квадратный корень:

${\displaystyle {\text{root }}\simeq {\frac {{\text{mean}}({\text{known square}},{\text{unknown square}})}{\text{known square root}}}\,}$

Вывод

По определению, если r — квадратный корень из x, то

${\displaystyle \mathrm {r} ^{2}=x\,\!}$

Затем переопределяется корень

${\displaystyle \mathrm {r} =a-b\,\!}$

где a — известный корень (4 из приведенного выше примера), а b — разница между известным корнем и искомым ответом.

${\displaystyle (a-b)^{2}=x\,\!}$

Увеличение доходности

${\displaystyle a^{2}-2ab+b^{2}=x\,\!}$

Если «a» близко к цели, «b» будет достаточно маленьким числом, чтобы сделать элемент уравнения незначительным. Таким образом, можно отбросить это уравнение и переставить его так: ${\displaystyle {}+b^{2}\,}$ ${\displaystyle {}+b^{2}\,}$

${\displaystyle b\simeq {\frac {a^{2}-x}{2a}}\,\!}$

и поэтому

${\displaystyle \mathrm {root} \simeq a-{\frac {a^{2}-x}{2a}}\,\!}$

которое можно свести к

${\displaystyle \mathrm {root} \simeq {\frac {a^{2}+x}{2a}}\,\!}$

Извлечение корней совершенных способностей

Часто практикуется извлечение корней совершенных способностей . Сложность задачи зависит не от количества разрядов совершенной степени, а от точности, т. е. количества разрядов корня. Кроме того, это зависит еще и от порядка корня; найти идеальные корни, в которых порядок корня взаимно прост с числом 10, несколько проще, поскольку цифры зашифрованы последовательным образом, как в следующем разделе.

Извлечение кубических корней

Легкая задача для новичка — извлечение кубических корней из кубов двузначных чисел. Например, зная 74088, определите, какое двузначное число, если его умножить на себя один раз, а затем еще раз умножить на это число, получится 74088. Тот, кто знает этот метод, быстро узнает, что ответ — 42, так как 42 ³ = 74088.

Перед изучением процедуры требуется, чтобы исполнитель запомнил кубики чисел 1-10:

Обратите внимание, что в самой правой цифре есть закономерность: сложение и вычитание с 1 или 3. Начиная с нуля:

• 0 ³ = 0
• 1 ³ = 1 вверх 1
• 2 ³ = 8 вниз 3
• 3 ³ = 2 7 вниз 1
• 4 ³ = 6 4 вниз 3
• 5 ³ = 12 5 вверх 1
• 6 ³ = 21 6 вверх 1
• 7 ³ = 34 3 вниз 3
• 8 ³ = 51 2 вниз 1
• 9 ³ = 72 9 вниз 3
• 10 ³ = 100 0 до 1

Извлечение кубического корня из куба двузначного числа состоит из двух шагов. Например, извлечение кубического корня из 29791. Определите место единицы (единицы) двузначного числа. Поскольку куб заканчивается цифрой 1, как показано выше, он должен быть равен 1.

• Если идеальный куб заканчивается на 0, то его кубический корень должен заканчиваться на 0.
• Если идеальный куб оканчивается на 1, то кубический корень из него должен заканчиваться на 1.
• Если идеальный куб оканчивается на 2, то кубический корень из него должен оканчиваться на 8.
• Если идеальный куб оканчивается цифрой 3, то кубический корень из него должен заканчиваться цифрой 7.
• Если идеальный куб оканчивается на 4, то его кубический корень должен оканчиваться на 4.
• Если идеальный куб оканчивается цифрой 5, то кубический корень из него должен заканчиваться цифрой 5.
• Если идеальный куб оканчивается цифрой 6, то кубический корень из него должен заканчиваться цифрой 6.
• Если идеальный куб оканчивается на 7, то кубический корень из него должен оканчиваться на 3.
• Если идеальный куб оканчивается на 8, то кубический корень из него должен оканчиваться на 2.
• Если идеальный куб оканчивается цифрой 9, то кубический корень из него должен заканчиваться цифрой 9.

Обратите внимание, что каждая цифра соответствует сама себе, за исключением 2, 3, 7 и 8, которые просто вычитаются из десяти, чтобы получить соответствующую цифру.

Второй шаг — определить первую цифру двузначного кубического корня, глядя на величину данного куба. Для этого удалим три последние цифры данного куба (29791 → 29) и найдем наибольший куб, которого он больше (вот тут-то и понадобится знание кубов чисел 1-10). Здесь 29 больше 1 в кубе, больше 2 в кубе, больше 3 в кубе, но не больше 4 в кубе. Наибольший куб, больше которого он равен 3, поэтому первая цифра двузначного куба должна быть 3.

Следовательно, кубический корень из 29791 равен 31.

Другой пример:

• Найдите кубический корень из числа 456533.
• Кубический корень оканчивается на 7.
• После того как отнимут три последние цифры, останется 456.
• 456 больше всех кубов до 7 в кубе.
• Первая цифра кубического корня равна 7.
• Кубический корень из 456533 равен 77.

Этот процесс можно расширить для поиска кубических корней длиной 3 цифры, используя арифметику по модулю 11. ^[4]

Эти типы трюков можно использовать с любым корнем, порядок которого взаимно прост с 10; таким образом, он не может работать с квадратным корнем, поскольку степень 2 делится на 10. 3 не делит 10, поэтому кубические корни работают.

Аппроксимация десятичных логарифмов (логарифм по основанию 10)

Чтобы приблизить десятичный логарифм (с точностью хотя бы до одной десятичной точки), требуется несколько правил логарифма и запоминание нескольких логарифмов. Человек должен знать:

• журнал(а × б) = журнал(а) + журнал(б)
• журнал(а/б) = журнал(а) - журнал(б)
• журнал (0) не существует
• журнал (1) = 0
• журнал(2) ~ .30
• журнал(3) ~ .48
• журнал(7) ~ 0,85

По этой информации можно найти логарифм любого числа от 1 до 9.

• журнал (1) = 0
• журнал(2) ~ .30
• журнал(3) ~ .48
• журнал(4) = журнал(2 × 2) = журнал(2) + журнал(2) ~ 0,60
• журнал (5) = журнал (10/2) = журнал (10) − журнал (2) ~ 0,70
• журнал(6) = журнал(2 × 3) = журнал(2) + журнал(3) ~ 0,78
• журнал(7) ~ 0,85
• log(8) = log(2 × 2 × 2) = log(2) + log(2) + log(2) ~ 0,90
• журнал(9) = журнал(3 × 3) = журнал(3) + журнал(3) ~ 0,96
• журнал(10) = 1 + журнал(1) = 1

Первым шагом в приближении десятого логарифма является приведение числа в научной форме. Например, число 45 в научной записи равно 4,5 × 10 ¹ , но будем называть его a × 10 ^b . Затем найдите логарифм числа а, которое находится между 1 и 10. Начните с нахождения логарифма числа 4, которое равно 0,60, а затем логарифма числа 5, которое равно 0,70, потому что между этими двумя находится 4,5. Далее, навыки в этом приходят с практикой, поместите 5 по логарифмической шкале между 0,6 и 0,7, где-то около 0,653 (ПРИМЕЧАНИЕ: фактическое значение дополнительных мест всегда будет больше, чем если бы они были помещены в обычное место). то есть можно было бы ожидать, что он будет равен 0,650, потому что это половина пути, но вместо этого он будет немного больше, в данном случае 0,653). Как только вы получили логарифм a, просто добавьте к нему b, чтобы получить приближение обыкновенного логарифма. В этом случае a + b = 0,653 + 1 = 1,653. Фактическое значение log(45) ~ 1,65321.

Тот же процесс применяется для чисел от 0 до 1. Например, 0,045 будет записано как 4,5 × 10 ⁻² . Единственное отличие состоит в том, что b теперь отрицательное, поэтому прибавление единицы на самом деле означает вычитание. Это даст результат 0,653–2 или –1,347.

Ментальная арифметика как психологический навык

Физические нагрузки надлежащего уровня могут привести к увеличению производительности умственной задачи , например выполнения мысленных вычислений, выполняемых впоследствии. ^[5] Было показано, что высокий уровень физической активности отрицательно влияет на выполнение умственных задач. ^[6] Это означает, что слишком большая физическая работа может снизить точность и результативность математических вычислений в уме. Было доказано, что физиологические измерения, в частности ЭЭГ , полезны для определения умственной нагрузки . ^[7] Использование ЭЭГ в качестве показателя умственной нагрузки после различных уровней физической активности может помочь определить уровень физической нагрузки, который будет наиболее полезен для умственной деятельности. Предыдущая работа, проделанная Ранджаной Мехтой в Мичиганском технологическом университете, включает недавнее исследование, в котором участвовали участники, выполняющие одновременные умственные и физические задачи. ^[8] В этом исследовании изучалось влияние умственных требований на физическую работоспособность при различных уровнях физической нагрузки и в конечном итоге было обнаружено снижение физической работоспособности, когда умственные задачи выполнялись одновременно, с более значительным эффектом при более высоком уровне физической нагрузки. Процедура Брауна-Петерсона — широко известная задача, использующая ментальную арифметику. Эта процедура, в основном используемая в когнитивных экспериментах, предполагает, что мысленное вычитание полезно при проверке влияния поддерживающей репетиции на продолжительность кратковременной памяти .

Чемпионат мира по ментальным расчетам

Первый чемпионат мира по ментальным вычислениям состоялся в 1997 году. Это мероприятие повторяется каждый год. Он состоит из ряда различных задач, таких как сложение десяти десятизначных чисел, умножение двух восьмизначных чисел, вычисление квадратных корней, вычисление дней недели для заданных дат, вычисление кубических корней и некоторые неожиданные разные задачи.

Кубок мира по ментальным расчетам

Первые чемпионаты мира по ментальным вычислениям ( Mental Calculation World Cup ) ^[9] состоялись в 2004 году. Они повторяются раз в два года. Он состоит из шести различных задач: сложение десяти десятизначных чисел, умножение двух восьмизначных чисел, вычисление квадратных корней и вычисление дней недели для заданных дат, вычисление кубических корней, а также несколько неожиданных разных задач.

Мемориада – Всемирная Олимпиада по памяти, умственному вычислению и скорочтению

«Мемориад» ^[10] — первая площадка, объединяющая соревнования по «умственному счету», «памяти» и «фоточтению». Игры и соревнования проводятся в год Олимпийских игр, каждые четыре года.

Первый международный Мемориад прошел в Стамбуле , Турция, в 2008 году. Второй Мемориад прошел в Анталье , Турция, 24–25 ноября 2012 года. В нем приняли участие 89 участников из 20 стран. Всего награды и денежные премии были вручены по 10 номинациям; из них 5 категорий должны были заниматься мысленными вычислениями (мысленное сложение, ментальное умножение, мысленные квадратные корни (нецелые), мысленное вычисление календарных дат и Flash Anzan).

Смотрите также

• Правило Судного дня для расчета дня недели
• Ментальные счеты
• Ментальный калькулятор
• Соробан

Примечания

1. Обратите внимание, что эти однозначные числа на самом деле представляют собой остатки, которые можно получить, если разделить исходные операнды на 9, то есть каждый из них является результатом соответствующего операнда по модулю 9 .

Рекомендации

1. Чепрасов, Артем (3 сентября 2009 г.). О новом методе умножения и сокращениях. США: независимая издательская платформа CreateSpace. ISBN 9781448689330.
2. "На записи с... Артемом Чепрасовым". Северо-Западный Вестник . Архивировано из оригинала 15 января 2011 г. Проверено 1 июня 2015 г.
3. умножение двух чисел близко, ниже 100
4. Доррелл, Филип. «Как извлечь кубические корни из 9-значных чисел в уме». Усердно думая . Проверено 19 июля 2015 г.
5. Ламбурн, Кейт; Томпоровский, Филипп (2010). «Влияние возбуждения, вызванного физическими упражнениями, на выполнение когнитивных задач: метарегрессионный анализ». Исследования мозга . 1341 : 12–24. doi :10.1016/j.brainres.2010.03.091. PMID  20381468. S2CID  206324098.
6. Брисвальтер, Дж.; Арселин, Р.; Одиффрен, М.; Делинььер, Д. (1997). «Влияние физических упражнений на время простой реакции: влияние физической подготовки». Перцептивные и моторные навыки . 85 (3): 1019–27. дои : 10.2466/pms.1997.85.3.1019. PMID  9399313. S2CID  30781628.
7. Мурата, Ацуо (2005). «Попытка оценить умственную нагрузку с помощью вейвлет-преобразования ЭЭГ». Человеческий фактор: Журнал Общества человеческого фактора и эргономики . 47 (3): 498–508. дои : 10.1518/001872005774860096. PMID  16435692. S2CID  25313835.
8. Мехта, Ранджана К.; Нуссбаум, Мори А.; Агнью, Майкл Дж. (2012). «Зависимые от мышц и задачи реакции на одновременную физическую и умственную нагрузку во время прерывистой статической работы». Эргономика . 55 (10): 1166–79. дои : 10.1080/00140139.2012.703695. PMID  22849301. S2CID  38648671.
9. «Кубок мира по ментальным вычислениям - чемпионат мира по ментальным вычислениям» . www.recordholders.org .
10. "Мемориад". www.memoriad.com .

Внешние ссылки

• Кубок мира по ментальным расчетам
• Мемориад - Всемирные ментальные олимпиады
• Цурио-Мазойер, Натали; Песенти, Мауро; Заго, Лора; Кривелло, Фабрис; Мелле, Эммануэль; Самсон, Дана; Дюру, Брюно; Серон, Ксавьер; Мазойер, Бернар (2001). «Умственный расчет у вундеркинда поддерживается правыми префронтальными и медиальными височными областями». Природная неврология . 4 (1): 103–7. дои : 10.1038/82831. PMID  11135652. S2CID  23829063.
• Ривера, С.М.; Рейсс, Алабама; Эккерт, Массачусетс; Менон, В. (2005). «Изменения в развитии ментальной арифметики: свидетельства повышенной функциональной специализации в левой нижней теменной коре». Кора головного мозга . 15 (11): 1779–90. дои : 10.1093/cercor/bhi055 . ПМИД  15716474.