Метод многосеточного моделирования

Метод решения дифференциальных уравнений

В численном анализе многосеточный метод ( метод MG ) представляет собой алгоритм решения дифференциальных уравнений с использованием иерархии дискретизаций . Они являются примером класса методов, называемых многомасштабными методами , очень полезными в задачах, демонстрирующих множественные масштабы поведения. Например, многие базовые методы релаксации демонстрируют разные скорости сходимости для коротковолновых и длинноволновых компонентов, что предполагает, что эти разные масштабы следует обрабатывать по-разному, как в подходе анализа Фурье к многосетке. ^[1] Методы MG можно использовать как решатели, так и предобуславливатели .

Основная идея многосеточного метода заключается в ускорении сходимости базового итерационного метода (известного как релаксация, которая обычно уменьшает коротковолновую ошибку) путем глобальной коррекции аппроксимации решения мелкой сетки время от времени, достигаемой путем решения грубой задачи . Грубая задача, хотя и более дешевая в решении, похожа на задачу мелкой сетки тем, что она также имеет коротковолновые и длинноволновые ошибки. Ее также можно решить путем комбинации релаксации и обращения к еще более грубым сеткам. Этот рекурсивный процесс повторяется до тех пор, пока не будет достигнута сетка, где стоимость прямого решения там пренебрежимо мала по сравнению со стоимостью одного релаксационного развертки на мелкой сетке. Этот многосеточный цикл обычно уменьшает все компоненты ошибки на фиксированную величину, ограниченную значительно ниже единицы, независимо от размера ячейки мелкой сетки. Типичное применение многосеточного метода — численное решение эллиптических уравнений в частных производных в двух или более измерениях. ^[2]

Многосеточные методы могут применяться в сочетании с любым из распространенных методов дискретизации. Например, метод конечных элементов может быть преобразован в многосеточный метод. ^[3] В этих случаях многосеточные методы являются одними из самых быстрых методов решения, известных сегодня. В отличие от других методов, многосеточные методы являются общими в том, что они могут обрабатывать произвольные области и граничные условия . Они не зависят от разделимости уравнений или других специальных свойств уравнения. Они также широко использовались для более сложных несимметричных и нелинейных систем уравнений, таких как уравнения упругости Ламе или уравнения Навье -Стокса . ^[4]

Алгоритм

Визуализация итеративного алгоритма Multigrid для быстрой сходимости O(n).

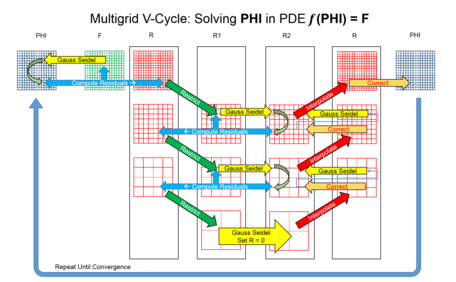
Существует множество вариаций многосеточных алгоритмов, но общими чертами является то, что рассматривается иерархия дискретизаций (сеток). Важные шаги: ^{[5] [6]}

• Сглаживание — уменьшение высокочастотных ошибок, например, с использованием нескольких итераций метода Гаусса–Зейделя .
• Остаточное вычисление – вычисление остаточной ошибки после операции(й) сглаживания.
• Ограничение – понижение разрешения остаточной ошибки до более грубой сетки.
• Интерполяция или продление — интерполяция поправки, вычисленной на более грубой сетке, на более мелкую сетку.
• Исправление – добавление более грубого решения на более мелкую сетку.

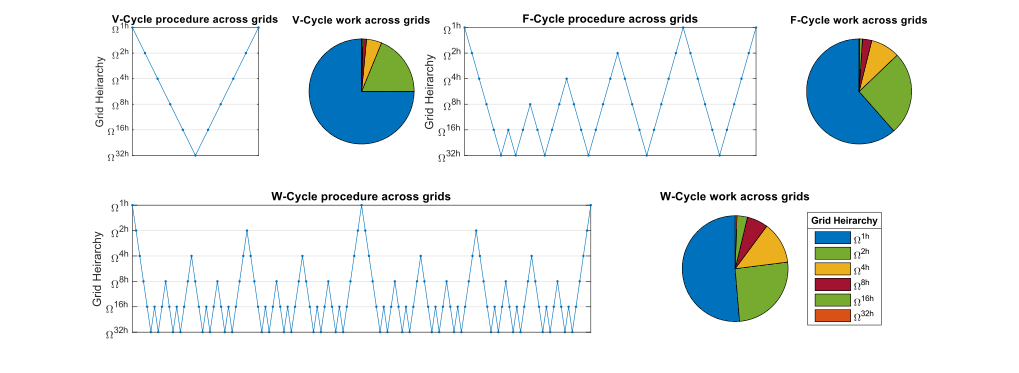
Существует множество вариантов многосеточных методов с различными компромиссами между скоростью решения одной итерации и скоростью сходимости с этой итерацией. 3 основных типа — V-цикл, F-цикл и W-цикл. Они различаются тем, какие и сколько циклов грубой зернистости выполняются на каждую тонкую итерацию. Алгоритм V-цикла выполняет один цикл грубой зернистости V-цикл. F-цикл выполняет цикл грубой зернистости V-цикла, за которым следует цикл грубой зернистости F-цикла, в то время как каждый цикл W-цикла выполняет два цикла грубой зернистости W-цикла на итерацию. Для дискретной 2D-задачи F-цикл занимает на 83% больше времени для вычисления, чем итерация V-цикла, в то время как итерация W-цикла занимает на 125% больше времени. Если задача ставится в трехмерной области, то итерация F-цикла и итерация W-цикла занимают примерно на 64% и 75% больше времени соответственно, чем итерация V-цикла, игнорируя накладные расходы . Обычно W-цикл обеспечивает сходимость, схожую с F-циклом. Однако в случаях задач конвекции-диффузии с высокими числами Пекле W-цикл может показать превосходство в скорости сходимости за итерацию над F-циклом. Выбор операторов сглаживания чрезвычайно разнообразен, поскольку они включают методы подпространства Крылова и могут быть предварительно обусловлены .

Любая геометрическая итерация многосеточного цикла выполняется на иерархии сеток и, следовательно, может быть закодирована с использованием рекурсии. Поскольку функция вызывает себя с параметрами меньшего размера (более грубыми), самая грубая сетка — это то место, где рекурсия останавливается. В случаях, когда система имеет высокое число условий , процедура коррекции изменяется таким образом, что только часть решения с более длинной грубой сеткой добавляется к более мелкой сетке.

Стоимость вычислений[ необходима ссылка ]

Если предположить, что задача двумерная, то вычисления по иерархии сеток происходят по-разному для различных многосеточных циклов.

Этот подход имеет преимущество перед другими методами, поскольку он часто масштабируется линейно с числом используемых дискретных узлов. Другими словами, он может решать эти проблемы с заданной точностью за число операций, пропорциональное числу неизвестных.

Предположим, что имеется дифференциальное уравнение, которое можно решить приближенно (с заданной точностью) на сетке с заданной плотностью точек сетки . Предположим далее, что решение на любой сетке может быть получено с заданными усилиями из решения на более грубой сетке . Здесь — отношение точек сетки на «соседних» сетках и предполагается постоянным по всей иерархии сетки, а — некоторая константа, моделирующая усилия по вычислению результата для одной точки сетки. ${\displaystyle i}$ ${\displaystyle N_{i}}$ ${\displaystyle N_{i}}$ ${\displaystyle W_{i}=\rho KN_{i}}$ ${\displaystyle i+1}$ ${\displaystyle \rho =N_{i+1}/N_{i}<1}$ ${\displaystyle K}$

Затем получается следующее рекуррентное соотношение для усилий по получению решения на сетке : ${\displaystyle k}$

${\displaystyle W_{k}=W_{k+1}+\rho KN_{k}}$

Пример скоростей сходимости многосеточных циклов в сравнении с другими операторами сглаживания.

И в частности, мы находим, что для самой мелкой сетки ${\displaystyle N_{1}}$

${\displaystyle W_{1}=W_{2}+\rho KN_{1}}$

Объединение этих двух выражений (и использование ) дает ${\displaystyle N_{k}=\rho ^{k-1}N_{1}}$

${\displaystyle W_{1}=KN_{1}\sum _{p=0}^{n}\rho ^{p}}$

Используя геометрическую прогрессию , мы затем находим (для конечных ) ${\displaystyle n}$

${\displaystyle W_{1}<KN_{1}{\frac {1}{1-\rho }}}$

то есть решение может быть получено со временем. Следует отметить, что есть одно исключение из многосетки W-цикла, используемой в одномерной задаче; это приведет к сложности. ^{[ необходима цитата ]} ${\displaystyle O(N)}$ ${\displaystyle O(N)}$ ${\displaystyle O(Nlog(N))}$

Многосеточная предварительная подготовка

Многосеточный метод с намеренно уменьшенной точностью может быть использован в качестве эффективного предобуславливателя для внешнего итерационного решателя, например, ^[7] Решение все еще может быть получено со временем, а также в случае, когда многосеточный метод используется в качестве решателя. Многосеточная предобуславливание используется на практике даже для линейных систем, как правило, с одним циклом на итерацию, например, в Hypre . Его основное преимущество по сравнению с чисто многосеточным решателем особенно очевидно для нелинейных задач, например, задач на собственные значения . ${\displaystyle O(N)}$

Если матрица исходного уравнения или задача на собственные значения симметрична и положительно определена (SPD), то предобуславливатель обычно строится так, чтобы он также был SPD, так что стандартные итерационные методы сопряженных градиентов (CG) все еще могут использоваться. Такие наложенные ограничения SPD могут усложнить построение предобуславливателя, например, требуя скоординированного предварительного и последующего сглаживания. Однако предобуславливающие методы наискорейшего спуска и гибкие методы CG для линейных систем SPD и LOBPCG для симметричных задач на собственные значения, как показано ^[8], являются надежными, если предобуславливатель не является SPD.

Предварительный кондиционер Брамбл-Пашьяк-Сюй

Первоначально описанный в докторской диссертации Сюй ^[9] и позднее опубликованный в Bramble-Pasciak-Xu, ^[10] предобуславливатель BPX является одним из двух основных многосеточных подходов (другой — классический многосеточный алгоритм, такой как V-цикл) для решения крупномасштабных алгебраических систем, возникающих из дискретизации моделей в науке и технике, описываемых уравнениями с частными производными. Ввиду структуры коррекции подпространства, ^[11] предобуславливатель BPX является параллельным методом коррекции подпространства, тогда как классический V-цикл является последовательным методом коррекции подпространства. Известно, что предобуславливатель BPX является естественно более параллельным и в некоторых приложениях более надежным, чем классический многосеточный метод V-цикла. Этот метод широко используется исследователями и практиками с 1990 года.

Обобщенные многосеточные методы

Многосеточные методы могут быть обобщены многими различными способами. Они могут быть применены естественным образом в шаговом по времени решении параболических уравнений в частных производных или они могут быть применены непосредственно к зависящим от времени уравнениям в частных производных . ^[12] Исследования многоуровневых методов для гиперболических уравнений в частных производных ведутся. ^[13] Многосеточные методы также могут быть применены к интегральным уравнениям или для задач статистической физики . ^[14]

Другой набор методов множественного разрешения основан на вейвлетах . Эти методы вейвлетов можно комбинировать с методами многосеточных вычислений. ^{[15] [16]} Например, одним из вариантов использования вейвлетов является переформулирование подхода конечных элементов в терминах многоуровневого метода. ^[17]

Адаптивная многосеточная модель демонстрирует адаптивное измельчение сетки , то есть она корректирует сетку по мере выполнения вычислений способом, зависящим от самих вычислений. ^[18] Идея состоит в том, чтобы увеличить разрешение сетки только в тех областях решения, где это необходимо.

Алгебраическая многосеточная (AMG)

Практически важные расширения многосеточных методов включают методы, в которых не используются ни дифференциальные уравнения в частных производных, ни геометрический фон проблемы для построения многоуровневой иерархии. ^[19] Такие алгебраические многосеточные методы (AMG) строят свою иерархию операторов непосредственно из системной матрицы. В классическом AMG уровни иерархии являются просто подмножествами неизвестных без какой-либо геометрической интерпретации. (В более общем смысле, неизвестные грубой сетки могут быть частными линейными комбинациями неизвестных тонкой сетки.) Таким образом, методы AMG становятся решателями черного ящика для определенных классов разреженных матриц . AMG считается выгодным в основном там, где геометрическую многосеточную систему слишком сложно применять, ^[20] но часто используется просто потому, что она избегает кодирования, необходимого для истинной многосеточной реализации. Хотя классический AMG был разработан первым, связанный алгебраический метод известен как сглаженная агрегация (SA).

В обзорной статье ^[21] Цзиньчао Сюй и Людмила Зикатанова «алгебраические многосеточные» методы рассматриваются с абстрактной точки зрения. Они разработали унифицированную структуру, и существующие алгебраические многосеточные методы могут быть выведены когерентно. Была выведена абстрактная теория о том, как построить оптимальное грубое пространство, а также квазиоптимальные пространства. Кроме того, они доказали, что при соответствующих предположениях абстрактный двухуровневый метод AMG сходится равномерно относительно размера линейной системы, вариации коэффициентов и анизотропии. Их абстрактная структура охватывает большинство существующих методов AMG, таких как классический AMG, AMG с минимизацией энергии, несглаженный и сглаженный агрегационный AMG и спектральный AMGe.

Многосеточные методы во времени

Многосеточные методы также были приняты для решения задач начального значения . ^[22] Особый интерес здесь представляют параллельные во времени многосеточные методы: ^[23] в отличие от классических методов Рунге–Кутты или линейных многошаговых методов, они могут предложить параллелизм во временном направлении. Хорошо известный метод параллельной интеграции Parareal во времени также может быть переформулирован как двухуровневая многосетка во времени.

Многосеточный подход для почти сингулярных задач

Почти сингулярные задачи возникают в ряде важных физических и инженерных приложений. Простой, но важный пример почти сингулярных задач можно найти в формулировке смещения линейной упругости для почти несжимаемых материалов. Как правило, основная проблема решения таких почти сингулярных систем сводится к обработке почти сингулярного оператора, заданного как , робастно относительно положительного, но малого параметра . Здесь — симметричный полуопределенный оператор с большим нулевым пространством , в то время как — симметричный положительно определенный оператор. Было много работ, направленных на попытку разработать надежный и быстрый многосеточный метод для таких почти сингулярных задач. Было предоставлено общее руководство в качестве принципа проектирования для достижения независимой от параметров (например, размера сетки и физических параметров, таких как коэффициент Пуассона , которые появляются в почти сингулярном операторе) скорости сходимости многосеточного метода, применяемого к таким почти сингулярным системам ^[24] , т. е. в каждой сетке пространственное разложение, на основе которого применяется сглаживание, должно быть построено таким образом, чтобы нулевое пространство сингулярной части почти сингулярного оператора было включено в сумму локальных нулевых пространств, пересечение нулевого пространства и локальных пространств, полученных в результате пространственных разложений. ${\displaystyle A+\varepsilon M}$ ${\displaystyle \varepsilon }$ ${\displaystyle A}$ ${\displaystyle M}$

Примечания

1. Роман Винандс; Вольфганг Йоппих (2005). Практический анализ Фурье для многосеточных методов. CRC Press. стр. 17. ISBN 978-1-58488-492-7.
2. У. Троттенберг; CW Остерли; А. Шуллер (2001). Многосеточный. Академическая пресса. ISBN 978-0-12-701070-0.
3. Ю Чжу; Андреас К. Кангелларис (2006). Многосеточные методы конечных элементов для моделирования электромагнитного поля. Wiley. стр. 132 и далее . ISBN 978-0-471-74110-7.
4. Шах, Тасним Мохаммад (1989). Анализ метода многосеточного анализа (диссертация). Оксфордский университет. Bibcode : 1989STIN...9123418S.
5. MT Heath (2002). "Раздел 11.5.7 Многосеточные методы". Научные вычисления: вводный обзор . McGraw-Hill Higher Education. стр. 478 и далее . ISBN 978-0-07-112229-0.
6. П. Весселинг (1992). Введение в многосеточные методы. Wiley. ISBN 978-0-471-93083-9.
7. Эндрю В. Князев, Клаус Неймейр. Эффективное решение симметричных задач на собственные значения с использованием многосеточных предобуславливателей в локально оптимальном методе блочных сопряженных градиентов. Electronic Transactions on Numerical Analysis, 15, 38–55, 2003.
8. Bouwmeester, Henricus; Dougherty, Andrew; Knyazev, Andrew V. (2015). «Несимметричное предварительное обусловливание для методов сопряженного градиента и наискорейшего спуска 1». Procedia Computer Science . 51 : 276–285. arXiv : 1212.6680 . doi : 10.1016/j.procs.2015.05.241 . S2CID  51978658.
9. Сюй, Цзиньчао. Теория многоуровневых методов. Т. 8924558. Итака, Нью-Йорк: Корнельский университет, 1989.
10. Брамбл, Джеймс Х., Джозеф Э. Пасциак и Цзиньчао Сюй. «Параллельные многоуровневые предобуславливатели». Математика вычислений 55, вып. 191 (1990): 1–22.
11. Сюй, Цзиньчао. «Итерационные методы с помощью пространственной декомпозиции и коррекции подпространства». Обзор SIAM 34, № 4 (1992): 581-613.
12. F. Hülsemann; M. Kowarschik; M. Mohr; U. Rüde (2006). "Параллельная геометрическая многосеточная модель". В Are Magnus Bruaset; Aslak Tveito (ред.). Численное решение уравнений с частными производными на параллельных компьютерах . Birkhäuser. стр. 165. ISBN 978-3-540-29076-6.
13. Например, J. Blaz̆ek (2001). Вычислительная гидродинамика: принципы и приложения. Elsevier. С. 305. ISBN 978-0-08-043009-6.и Ачи Брандт и Рима Гандлин (2003). "Многосеточный метод усвоения атмосферных данных: анализ". В Томасе И. Хоу; Эйтане Тадморе (ред.). Гиперболические задачи: теория, численные методы, приложения: труды Девятой международной конференции по гиперболическим задачам 2002 года . Springer. стр. 369. ISBN 978-3-540-44333-9.
14. Ачи Брандт (2002). "Многомасштабные научные вычисления: обзор". В Тимоти Дж. Барт; Тони Чан; Роберт Хеймс (ред.). Многомасштабные и многоразрешающие методы: теория и приложения . Springer. стр. 53. ISBN 978-3-540-42420-8.
15. Бьорн Энгквист; Олоф Ранборг (2002). "Численная гомогенизация на основе вейвлетов с приложениями". В Тимоти Дж. Барте; Тони Чане; Роберте Хеймсе (ред.). Методы многомасштабных и многоразрешающих методов . Том 20 Lecture Notes in Computational Science and Engineering. Springer. стр. 140 и далее . ISBN 978-3-540-42420-8.
16. У. Троттенберг; CW Остерли; А. Шуллер (2001). Многосеточный. Академическая пресса. ISBN 978-0-12-701070-0.
17. Альберт Коэн (2003). Численный анализ вейвлет-методов. Elsevier. стр. 44. ISBN 978-0-444-51124-9.
18. U. Trottenberg; CW Oosterlee; A. Schüller (2001). "Глава 9: Адаптивная многосеточная". Multigrid . Academic Press. стр. 356. ISBN 978-0-12-701070-0.
19. Яир Шапира (2003). "Алгебраическая многосеточная". Матричная многосеточная: теория и приложения . Springer. стр. 66. ISBN 978-1-4020-7485-1.
20. У. Троттенберг; CW Остерли; А. Шуллер (2001). Многосеточный. Академическая пресса. п. 417. ИСБН 978-0-12-701070-0.
21. Сюй Дж. и Зикатанов Л., 2017. Алгебраические многосеточные методы. Acta Numerica, 26, стр. 591–721. [1]
22. Хакбуш, Вольфганг (1985). «Параболические многосеточные методы». Computing Methods in Applied Sciences and Engineering, VI : 189–197. ISBN 9780444875976. Получено 1 августа 2015 г.
23. Хортон, Грэм (1992). «Метод многосеточных параллельных во времени» (The time-parallel multigrid method). Сообщения по прикладным численным методам . 8 (9): 585–595. doi :10.1002/cnm.1630080906.
24. Young-Ju Lee, Jinbiao Wu, Jinchao Xu и Ludmil Zikatanov, Robust Subspace Correction Methods for Almost Singular Systems, Mathematical Models and Methods in Applied Sciences, Vol. 17, No 11, pp. 1937-1963 (2007)

Ссылки

• ГП Астраханцев (1971), Итерационный метод решения эллиптических сеточных задач. Сборник научных трудов СССР. Математическая физика, 11, 171–182.
• Н. С. Бахвалов (1966), О сходимости метода релаксации с естественными ограничениями на эллиптический оператор, Сборник научных трудов СССР, 6, 101–113.
• Ачи Брандт (апрель 1977 г.), «Многоуровневые адаптивные решения граничных задач», Математика вычислений , 31 : 333–90.
• Уильям Л. Бриггс, Ван Эмден Хенсон и Стив Ф. Маккормик (2000), Учебное пособие по многосеткам (2-е изд.), Филадельфия: Общество промышленной и прикладной математики , ISBN 0-89871-462-1 . 
• Р. П. Федоренко (1961), Релаксационный метод решения эллиптических разностных уравнений. Журнал вычислительной математики и физики СССР, т. 1, стр. 1092.
• Р. П. Федоренко (1964), Скорость сходимости одного итерационного процесса. Журнал вычислительной математики и физики СССР, т. 4, стр. 227.
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Раздел 20.6. Многосеточные методы для граничных задач". Numerical Recipes: The Art of Scientific Computing (3-е изд.). Нью-Йорк: Cambridge University Press. ISBN 978-0-521-88068-8.

Внешние ссылки

• Репозиторий для многосеточных, многоуровневых, многомасштабных методов, методов агрегации, исправления дефектов и декомпозиции доменов
• Учебник по Multigrid
• Учебник по алгебраическим многосеткам
• Ссылки на презентации AMG