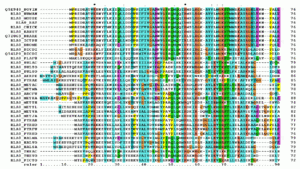
Множественное выравнивание последовательностей

Выравнивание более двух молекулярных последовательностей

Первые 90 позиций множественного выравнивания последовательностей белков кислого рибосомального белка P0 (L10E) из нескольких организмов. Сгенерировано с помощью Clustal X.

Множественное выравнивание последовательностей ( MSA ) — это процесс или результат выравнивания последовательностей трех или более биологических последовательностей , как правило, белков , ДНК или РНК . Эти выравнивания используются для вывода эволюционных связей с помощью филогенетического анализа и могут выделить гомологичные черты между последовательностями. Выравнивания выделяют мутационные события, такие как точечные мутации (изменения одной аминокислоты или нуклеотида ), мутации вставки и мутации делеции , а выравнивания используются для оценки сохранения последовательностей и вывода наличия и активности доменов белка , третичных структур , вторичных структур и отдельных аминокислот или нуклеотидов.

Множественные выравнивания последовательностей требуют более сложных методологий, чем парные выравнивания , поскольку они более сложны в вычислительном отношении . Большинство программ множественного выравнивания последовательностей используют эвристические методы, а не глобальную оптимизацию , поскольку определение оптимального выравнивания между несколькими последовательностями умеренной длины является недопустимо затратным в вычислительном отношении. Однако эвристические методы, как правило, не могут гарантировать высококачественные решения и, как было показано, не дают почти оптимальных решений в контрольных тестовых случаях. ^{[1] [2] [3]}

Постановка проблемы

Даны последовательности , подобные приведенной ниже форме: ${\displaystyle m}$ ${\displaystyle S_{i}}$ ${\displaystyle i=1,\cdots ,m}$

${\displaystyle S:={\begin{cases}S_{1}=(S_{11},S_{12},\ldots ,S_{1n_{1}})\\S_{2}=(S_{21},S_{22},\cdots ,S_{2n_{2}})\\\,\,\,\,\,\,\,\,\,\,\vdots \\S_{m}=(S_{m1},S_{m2},\ldots ,S_{mn_{m}})\end{cases}}}$

Множественное выравнивание последовательностей выполняется из этого набора последовательностей путем вставки любого количества необходимых пробелов в каждую из последовательностей до тех пор, пока все измененные последовательности, , не будут соответствовать длине и ни одно значение в последовательностях того же столбца не будет состоять только из пробелов. Математическая форма MSA для вышеуказанного набора последовательностей показана ниже: ${\displaystyle S}$ ${\displaystyle S_{i}}$ ${\displaystyle S}$ ${\displaystyle S'_{i}}$ ${\displaystyle L\geq \max\{n_{i}\mid i=1,\ldots ,m\}}$ ${\displaystyle S}$

${\displaystyle S':={\begin{cases}S'_{1}=(S'_{11},S'_{12},\ldots ,S'_{1L})\\S'_{2}=(S'_{21},S'_{22},\ldots ,S'_{2L})\\\,\,\,\,\,\,\,\,\,\,\vdots \\S'_{m}=(S'_{m1},S'_{m2},\ldots ,S'_{mL})\end{cases}}}$

Чтобы вернуться из каждой конкретной последовательности в , удалите все пробелы. ${\displaystyle S'_{i}}$ ${\displaystyle S_{i}}$

Графический подход

Общий подход при вычислении множественных выравниваний последовательностей заключается в использовании графов для идентификации всех различных выравниваний. При поиске выравниваний с помощью графа полное выравнивание создается в взвешенном графе, содержащем набор вершин и набор ребер. Каждое из ребер графа имеет вес, основанный на определенной эвристике, которая помогает оценить каждое выравнивание или подмножество исходного графа.

Трассировка выравниваний

При определении наиболее подходящих выравниваний для каждого MSA обычно генерируется трасса . Трасса — это набор реализованных или соответствующих и выровненных вершин, имеющих определенный вес на основе ребер, выбранных между соответствующими вершинами. При выборе трасс для набора последовательностей необходимо выбрать трассу с максимальным весом, чтобы получить наилучшее выравнивание последовательностей.

Методы выравнивания

Существуют различные методы выравнивания, используемые в нескольких последовательностях для максимизации оценок и правильности выравниваний. Каждый из них обычно основан на определенной эвристике с пониманием эволюционного процесса. Большинство пытаются воспроизвести эволюцию, чтобы получить максимально реалистичное выравнивание для наилучшего прогнозирования отношений между последовательностями.

Динамическое программирование

Прямой метод получения MSA использует метод динамического программирования для определения глобально оптимального решения для выравнивания. Для белков этот метод обычно включает два набора параметров: штраф за пробел и матрицу замещения, назначающую баллы или вероятности выравниванию каждой возможной пары аминокислот на основе сходства химических свойств аминокислот и эволюционной вероятности мутации. Для нуклеотидных последовательностей используется аналогичный штраф за пробел, но типична гораздо более простая матрица замещения, в которой учитываются только идентичные совпадения и несовпадения. Баллы в матрице замещения могут быть либо полностью положительными, либо смесью положительных и отрицательных в случае глобального выравнивания, но должны быть как положительными, так и отрицательными в случае локального выравнивания. ^[4]

Для n отдельных последовательностей наивный метод требует построения n -мерного эквивалента матрицы, сформированной в стандартном попарном выравнивании последовательностей . Таким образом, пространство поиска увеличивается экспоненциально с ростом n и также сильно зависит от длины последовательности. Выраженное с помощью большой нотации O, обычно используемой для измерения вычислительной сложности , наивный MSA занимает O(Длина ^Nseqs ) времени для создания. Было показано, что нахождение глобального оптимума для n последовательностей таким способом является NP-полной задачей. ^{[5] [6] [7]} В 1989 году на основе алгоритма Каррильо-Липмана ^[8] Альтшуль представил практический метод, который использует попарные выравнивания для ограничения n-мерного пространства поиска. ^[9] В этом подходе попарные динамические программные выравнивания выполняются для каждой пары последовательностей в наборе запроса, и только пространство вблизи n-мерного пересечения этих выравниваний ищется для n-стороннего выравнивания. Программа MSA оптимизирует сумму всех пар символов в каждой позиции в выравнивании (так называемая сумма парных оценок) и была реализована в программном обеспечении для построения множественных выравниваний последовательностей. ^[10] В 2019 году Хоссейнинасаб и ван Хув показали, что с помощью диаграмм решений MSA можно моделировать в полиномиальном пространстве сложности. ^[3]

Прогрессивное выравнивание конструкции

Наиболее широко используемый подход к множественным выравниваниям последовательностей использует эвристический поиск, известный как прогрессивный метод (также известный как иерархический или древовидный метод), разработанный Да-Фэй Фэном и Дулитлом в 1987 году. ^[11] Прогрессивное выравнивание создает окончательный MSA путем объединения попарных выравниваний, начиная с наиболее похожей пары и продвигаясь к наиболее отдаленно связанной. Все методы прогрессивного выравнивания требуют двух этапов: первый этап, на котором отношения между последовательностями представлены в виде филогенетического дерева , называемого направляющим деревом , и второй этап, на котором MSA строится путем последовательного добавления последовательностей к растущему MSA в соответствии с направляющим деревом. Начальное направляющее дерево определяется эффективным методом кластеризации , таким как метод объединения соседей или невзвешенный метод парной группы со средним арифметическим ( UPGMA ), и может использовать расстояния, основанные на количестве идентичных двухбуквенных подпоследовательностей (как в FASTA , а не динамическом программном выравнивании). ^[12]

Прогрессивные выравнивания не гарантируют глобальной оптимальности. Основная проблема заключается в том, что когда на любом этапе выращивания MSA допускаются ошибки, эти ошибки затем распространяются на конечный результат. Производительность также особенно плоха, когда все последовательности в наборе довольно отдаленно связаны. Большинство современных прогрессивных методов изменяют свою функцию подсчета с помощью вторичной весовой функции, которая назначает коэффициенты масштабирования отдельным членам набора запроса нелинейным образом на основе их филогенетического расстояния от ближайших соседей. Это исправляет неслучайный выбор последовательностей, заданных для программы выравнивания. ^[12]

Методы прогрессивного выравнивания достаточно эффективны для внедрения в больших масштабах для многих последовательностей (от сотен до тысяч). Популярным методом прогрессивного выравнивания является семейство Clustal . ^{[13] [14]} Clustal W широко используется для построения филогенетического дерева, несмотря на явные предупреждения автора о том, что неотредактированные выравнивания не следует использовать в таких исследованиях и в качестве входных данных для прогнозирования структуры белка с помощью моделирования гомологии. Европейский институт биоинформатики (EMBL-EBI) объявил, что срок действия CLustalW2 истекает в августе 2015 года. Они рекомендуют Clustal Omega, который работает на основе направляющих деревьев с семенами и методов HMM profile-profile для выравнивания белков. Альтернативным инструментом для прогрессивного выравнивания ДНК является множественное выравнивание с использованием быстрого преобразования Фурье ( MAFFT ). ^[15]

Другой распространенный метод прогрессивного выравнивания, называемый T-Coffee ^[16] , медленнее, чем Clustal и его производные, но, как правило, производит более точные выравнивания для наборов отдаленно связанных последовательностей. T-Coffee вычисляет попарные выравнивания, комбинируя прямое выравнивание пары с косвенными выравниваниями, которые выравнивают каждую последовательность пары с третьей последовательностью. Он использует выходные данные Clustal, а также другую программу локального выравнивания LALIGN, которая находит несколько областей локального выравнивания между двумя последовательностями. Полученное выравнивание и филогенетическое дерево используются в качестве руководства для создания новых и более точных весовых коэффициентов.

Поскольку прогрессивные методы являются эвристиками, которые не гарантированно сходятся к глобальному оптимуму, качество выравнивания может быть трудно оценить, а их истинное биологическое значение может быть неясным. Полупрогрессивный метод, который улучшает качество выравнивания и не использует эвристику с потерями при работе в полиномиальном времени, был реализован в программе PSAlign. ^[17]

Итерационные методы

Набор методов для создания MSA, одновременно уменьшая ошибки, присущие прогрессивным методам, классифицируется как «итеративный», поскольку они работают аналогично прогрессивным методам, но многократно перестраивают исходные последовательности, а также добавляют новые последовательности к растущей MSA. Одной из причин, по которой прогрессивные методы так сильно зависят от высококачественного начального выравнивания, является тот факт, что эти выравнивания всегда включаются в конечный результат — то есть, как только последовательность была выровнена в MSA, ее выравнивание далее не рассматривается. Это приближение повышает эффективность за счет точности. Напротив, итеративные методы могут возвращаться к ранее рассчитанным парным выравниваниям или под-MSA, включающим подмножества последовательности запроса в качестве средства оптимизации общей целевой функции, такой как поиск высококачественной оценки выравнивания. ^[12]

Множество тонко различающихся методов итерации были реализованы и стали доступны в программных пакетах; обзоры и сравнения были полезны, но, как правило, воздерживаются от выбора «лучшей» методики. ^[18] Программный пакет PRRN/PRRP использует алгоритм восхождения на вершину для оптимизации своей оценки выравнивания MSA ^[19] и итеративно корректирует как веса выравнивания, так и локально расходящиеся или «разрывные» области растущей MSA. ^[12] PRRP работает лучше всего при уточнении выравнивания, ранее построенного более быстрым методом. ^[12]

Другая итеративная программа, DIALIGN, использует необычный подход, фокусируясь только на локальных выравниваниях между подсегментами или мотивами последовательностей без введения штрафа за пробелы. ^[20] Затем выравнивание отдельных мотивов достигается с помощью матричного представления, похожего на точечно-матричный график в парном выравнивании. Альтернативный метод, который использует быстрые локальные выравнивания в качестве опорных точек или семян для более медленной процедуры глобального выравнивания, реализован в наборе CHAOS/DIALIGN. ^[20]

Третий популярный метод, основанный на итерациях, называемый MUSCLE (множественное выравнивание последовательностей с помощью логарифмического ожидания), улучшает прогрессивные методы с помощью более точной меры расстояния для оценки родства двух последовательностей. ^[21] Мера расстояния обновляется между этапами итерации (хотя в своей первоначальной форме MUSCLE содержал только 2-3 итерации в зависимости от того, было ли включено уточнение).

Методы консенсуса

Методы консенсуса пытаются найти оптимальное множественное выравнивание последовательностей, учитывая несколько различных выравниваний одного и того же набора последовательностей. Существует два широко используемых метода консенсуса: M-COFFEE и MergeAlign. ^[22] M-COFFEE использует множественные выравнивания последовательностей, созданные семью различными методами, для создания консенсусных выравниваний. MergeAlign способен генерировать консенсусные выравнивания из любого количества входных выравниваний, созданных с использованием различных моделей эволюции последовательностей или различных методов множественного выравнивания последовательностей. Параметр по умолчанию для MergeAlign — вывести консенсусное выравнивание с использованием выравниваний, созданных с использованием 91 различных моделей эволюции последовательностей белков.

Скрытые марковские модели

Профиль скрытой марковской модели (HMM), моделирующей множественное выравнивание последовательностей

Скрытая марковская модель (HMM) — вероятностная модель, которая может назначать вероятности всем возможным комбинациям пробелов, совпадений и несовпадений, чтобы определить наиболее вероятный MSA или набор возможных MSA. HMM могут производить один выход с наивысшей оценкой, но также могут генерировать семейство возможных выравниваний, которые затем могут быть оценены на предмет биологической значимости. HMM могут производить как глобальные, так и локальные выравнивания. Хотя методы на основе HMM были разработаны относительно недавно, они предлагают значительные улучшения в скорости вычислений, особенно для последовательностей, которые содержат перекрывающиеся области. ^[12]

Типичные методы на основе HMM работают, представляя MSA как форму направленного ациклического графа, известного как граф частичного порядка, который состоит из ряда узлов, представляющих возможные записи в столбцах MSA. В этом представлении столбец, который является абсолютно консервативным (то есть, что все последовательности в MSA разделяют определенный символ в определенной позиции), кодируется как один узел с таким количеством исходящих соединений, сколько возможных символов в следующем столбце выравнивания. В терминах типичной скрытой марковской модели наблюдаемые состояния являются отдельными столбцами выравнивания, а «скрытые» состояния представляют предполагаемую предковую последовательность, от которой, как предполагается, произошли последовательности в наборе запроса. Эффективный поисковый вариант метода динамического программирования, называемый алгоритмом Витерби , обычно используется для последовательного выравнивания растущего MSA со следующей последовательностью в наборе запроса для создания нового MSA. ^[23] Это отличается от методов прогрессивного выравнивания, поскольку выравнивание предыдущих последовательностей обновляется при каждом добавлении новой последовательности. Однако, как и в случае с прогрессивными методами, на этот метод может влиять порядок, в котором последовательности в наборе запроса интегрируются в выравнивание, особенно когда последовательности имеют отдаленное родство. ^[12]

Доступно несколько программ, в которых реализованы варианты методов на основе HMM, и которые известны своей масштабируемостью и эффективностью, хотя правильное использование метода HMM сложнее, чем использование более распространенных прогрессивных методов. Самым простым является выравнивание частичного порядка (POA), ^[24] и аналогичный более общий метод реализован в программном пакете Sequence Alignment and Modeling System (SAM). ^[25] и HMMER . ^[26] SAM использовался в качестве источника выравниваний для предсказания структуры белка для участия в эксперименте по предсказанию структуры Critical Assessment of Structure Prediction ( CASP ) и для разработки базы данных предсказанных белков в дрожжах вида S. cerevisiae . HHsearch ^[27] — это программный пакет для обнаружения отдаленно связанных последовательностей белков на основе попарного сравнения HMM. Сервер, на котором работает HHsearch ( HHpred ), был самым быстрым из 10 серверов автоматического предсказания структуры в соревнованиях по предсказанию структуры CASP7 и CASP8. ^[28]

Методы, учитывающие филогению

Негомологичное выравнивание экзонов итеративным методом (а) и методом, учитывающим филогению (б)

Большинство методов выравнивания множественных последовательностей пытаются минимизировать количество вставок/делеций (пробелов) и, как следствие, производить компактные выравнивания. Это вызывает несколько проблем, если последовательности, которые должны быть выровнены, содержат негомологичные области , если пробелы информативны в анализе филогении . Эти проблемы распространены в недавно созданных последовательностях, которые плохо аннотированы и могут содержать сдвиги рамки считывания , неправильные домены или негомологичные сплайсированные экзоны . Первый такой метод был разработан в 2005 году Лёйтинойей и Голдманом. ^[29] Те же авторы выпустили программный пакет под названием PRANK в 2008 году. ^[30] PRANK улучшает выравнивания при наличии вставок. Тем не менее, он работает медленно по сравнению с прогрессивными и/или итеративными методами, которые разрабатывались в течение нескольких лет.

В 2012 году появились два новых инструмента, учитывающих филогению. Один из них называется PAGAN и был разработан той же командой, что и PRANK. ^[31] Другой — ProGraphMSA , разработанный Шалковски. ^[32] Оба пакета программного обеспечения были разработаны независимо, но имеют общие черты, в частности, использование графовых алгоритмов для улучшения распознавания негомологичных регионов и улучшение кода, делающее это программное обеспечение быстрее PRANK.

Поиск мотива

Выравнивание семи каспаз Drosophila , окрашенных мотивами, как идентифицировано MEME. Когда позиции мотивов и выравнивания последовательностей генерируются независимо, они часто хорошо коррелируют, но не идеально, как в этом примере.

Поиск мотивов, также известный как профильный анализ, представляет собой метод обнаружения мотивов последовательностей в глобальных MSA, который является как средством создания лучшего MSA, так и средством создания матрицы оценки для использования при поиске других последовательностей для похожих мотивов. Было разработано множество методов изоляции мотивов, но все они основаны на идентификации коротких высококонсервативных шаблонов в пределах большего выравнивания и построении матрицы, аналогичной матрице замены, которая отражает аминокислотный или нуклеотидный состав каждой позиции в предполагаемом мотиве. Затем выравнивание можно уточнить с помощью этих матриц. В стандартном профильном анализе матрица включает записи для каждого возможного символа, а также записи для пробелов. ^[12] В качестве альтернативы статистические алгоритмы поиска шаблонов могут идентифицировать мотивы как предшественника MSA, а не как производное. Во многих случаях, когда набор запросов содержит только небольшое количество последовательностей или содержит только высокосвязанные последовательности, добавляются псевдосчетчики для нормализации распределения, отраженного в матрице оценок. В частности, это исправляет записи с нулевой вероятностью в матрице до значений, которые являются малыми, но ненулевыми.

Анализ блоков — это метод поиска мотивов, который ограничивает мотивы непропущенными областями в выравнивании. Блоки могут быть сгенерированы из MSA или могут быть извлечены из невыровненных последовательностей с использованием предварительно рассчитанного набора общих мотивов, ранее сгенерированных из известных семейств генов. ^[33] Оценка блоков обычно основана на интервалах между высокочастотными символами, а не на расчете явной матрицы замещения.

Статистическое сопоставление шаблонов было реализовано с использованием как алгоритма максимизации ожиданий, так и сэмплера Гиббса . Один из наиболее распространенных инструментов поиска мотивов, называемый Multiple EM for Motif Elicitation (MEME), использует максимизацию ожиданий и скрытые методы Маркова для генерации мотивов, которые затем используются в качестве инструментов поиска его компаньоном MAST в объединенном наборе MEME/MAST. ^{[34] [35]}

Некодирующее множественное выравнивание последовательностей

Некодирующие области ДНК, особенно сайты связывания факторов транскрипции (TFBS), являются консервативными, но не обязательно эволюционно связанными и могли конвергировать от необщих предков. Таким образом, предположения, используемые для выравнивания последовательностей белков и кодирующих областей ДНК, по своей сути отличаются от тех, которые справедливы для последовательностей TFBS. Хотя выравнивание кодирующих областей ДНК для гомологичных последовательностей с использованием операторов мутации имеет смысл, выравнивание последовательностей сайтов связывания для одного и того же фактора транскрипции не может полагаться на эволюционно связанные операции мутации. Аналогично, эволюционный оператор точечных мутаций может использоваться для определения расстояния редактирования для кодирующих последовательностей, но это имеет мало смысла для последовательностей TFBS, поскольку любая вариация последовательности должна поддерживать определенный уровень специфичности для функционирования сайта связывания. Это становится особенно важным при попытке выравнивания известных последовательностей TFBS для построения контролируемых моделей для прогнозирования неизвестных местоположений тех же TFBS. Следовательно, методы множественного выравнивания последовательностей должны корректировать базовую эволюционную гипотезу и операторы, используемые, как в опубликованной работе, включающей соседнюю базовую термодинамическую информацию ^[36], чтобы выровнять сайты связывания, находя самое низкое термодинамическое выравнивание, сохраняющее специфичность сайта связывания.

Оптимизация

Генетические алгоритмы и имитация отжига

Стандартные методы оптимизации в компьютерной науке — оба из которых были вдохновлены, но не воспроизводят напрямую физические процессы — также использовались в попытке более эффективно производить качественные MSA. Один из таких методов, генетические алгоритмы , использовался для производства MSA в попытке широко имитировать предполагаемый эволюционный процесс, который привел к расхождению в наборе запросов. Метод работает путем разбиения ряда возможных MSA на фрагменты и многократной перестановки этих фрагментов с введением пробелов в различных позициях. Общая целевая функция оптимизируется во время моделирования, в основном это функция максимизации «суммы пар», введенная в методах MSA на основе динамического программирования. Метод для последовательностей белков был реализован в программном обеспечении SAGA (Sequence Alignment by Genetic Algorithm) ^[37] , а его эквивалент в РНК называется RAGA. ^[38]

Метод имитации отжига , при котором существующий MSA, полученный другим методом, совершенствуется серией перестроек, разработанных для поиска лучших областей пространства выравнивания, чем та, которую уже занимает входное выравнивание. Как и метод генетического алгоритма, имитация отжига максимизирует целевую функцию, такую ​​как функция суммы пар. Имитация отжига использует метафорический «температурный фактор», который определяет скорость, с которой происходят перестройки, и вероятность каждой перестройки; типичное использование чередует периоды высоких скоростей перестройки с относительно низкой вероятностью (для исследования более отдаленных областей пространства выравнивания) с периодами более низких скоростей и более высоких вероятностей для более тщательного исследования локальных минимумов вблизи недавно «колонизированных» областей. Этот подход был реализован в программе MSASA (Multiple Sequence Alignment by Simulated Annealing). ^[39]

Математическое программирование и точные алгоритмы решения

Математическое программирование и, в частности, модели смешанного целочисленного программирования являются еще одним подходом к решению задач MSA. Преимущество таких моделей оптимизации заключается в том, что их можно использовать для поиска оптимального решения MSA более эффективно по сравнению с традиционным подходом DP. Это отчасти связано с применимостью методов декомпозиции для математических программ, где модель MSA разлагается на более мелкие части и итеративно решается до тех пор, пока не будет найдено оптимальное решение. Примеры алгоритмов, используемых для решения моделей смешанного целочисленного программирования MSA, включают в себя ветвь и цену ^[40] и декомпозицию Бендерса . ^[3] Хотя точные подходы вычислительно медленны по сравнению с эвристическими алгоритмами для MSA, они гарантированно достигают оптимального решения в конечном итоге, даже для задач большого размера.

Моделирование квантовых вычислений

В январе 2017 года компания D-Wave Systems объявила, что ее программное обеспечение для квантовых вычислений с открытым исходным кодом qbsolv было успешно использовано для поиска более быстрого решения проблемы MSA. ^[41]

Визуализация выравнивания и контроль качества

Необходимое использование эвристики для множественного выравнивания означает, что для произвольного набора белков всегда есть большая вероятность того, что выравнивание будет содержать ошибки. Например, оценка нескольких ведущих программ выравнивания с использованием бенчмарка BAliBase показала, что по крайней мере 24% всех пар выровненных аминокислот были выровнены неправильно. ^[2] Эти ошибки могут возникать из-за уникальных вставок в один или несколько регионов последовательностей или из-за какого-то более сложного эволюционного процесса, приводящего к белкам, которые нелегко выравниваются только по последовательности. По мере увеличения количества последовательностей и их расхождения будет сделано еще больше ошибок просто из-за эвристической природы алгоритмов MSA. Просмотрщики множественных выравниваний последовательностей позволяют визуально просматривать выравнивания, часто путем проверки качества выравнивания для аннотированных функциональных участков на двух или более последовательностях. Многие также позволяют редактировать выравнивание, чтобы исправить эти (обычно незначительные) ошибки, чтобы получить оптимальное «курируемое» выравнивание, подходящее для использования в филогенетическом анализе или сравнительном моделировании. ^[42]

Однако по мере увеличения числа последовательностей, особенно в полногеномных исследованиях, включающих множество MSA, становится невозможно вручную курировать все выравнивания. Кроме того, ручное курирование субъективно. И, наконец, даже лучший эксперт не может уверенно выравнивать более неоднозначные случаи сильно расходящихся последовательностей. В таких случаях обычной практикой является использование автоматических процедур для исключения ненадежно выровненных областей из MSA. Для реконструкции филогении (см. ниже) программа Gblocks широко используется для удаления блоков выравнивания, подозреваемых в низком качестве, в соответствии с различными пороговыми значениями количества пропущенных последовательностей в столбцах выравнивания. ^[43] Однако эти критерии могут чрезмерно отфильтровывать области с событиями вставки/удаления, которые все еще могут быть надежно выровнены, и эти области могут быть желательны для других целей, таких как обнаружение положительного отбора. Несколько алгоритмов выравнивания выводят сайт-специфичные оценки, которые позволяют выбирать области с высокой степенью достоверности. Такая услуга была впервые предложена программой SOAP ^[44] , которая проверяет устойчивость каждого столбца к возмущению параметров популярной программы выравнивания CLUSTALW. Программа T-Coffee ^[45] использует библиотеку выравниваний при построении окончательного MSA, и ее выходной MSA окрашен в соответствии с оценками достоверности, которые отражают согласие между различными выравниваниями в библиотеке относительно каждого выровненного остатка. Ее расширение, Transitive Consistency Score (TCS), использует библиотеки парных выравниваний T-Coffee для оценки любого стороннего MSA. Парные проекции могут быть получены с использованием быстрых или медленных методов, что позволяет найти компромисс между скоростью и точностью. ^{[46] [47]} Другая программа выравнивания, которая может выводить MSA с оценками достоверности, — это FSA ^[48] , которая использует статистическую модель, позволяющую вычислять неопределенность в выравнивании. Оценка HoT (Heads-Or-Tails) может использоваться в качестве меры неопределенности выравнивания, специфичной для сайта, из-за существования нескольких кооптимальных решений. ^[49] Программа GUIDANCE ^[50] вычисляет похожую меру достоверности, специфичную для сайта, на основе надежности выравнивания к неопределенности в направляющем дереве, которое используется в программах прогрессивного выравнивания. Альтернативный, более статистически обоснованный подход к оценке неопределенности выравнивания — это использование вероятностных эволюционных моделей для совместной оценки филогении и выравнивания. Байесовский подход позволяет вычислять апостериорные вероятности оцененной филогении и выравнивания, что является мерой достоверности этих оценок. В этом случае апостериорную вероятность можно рассчитать для каждого сайта в выравнивании. Такой подход был реализован в программе BAli-Phy. ^[51]

Существуют бесплатные программы для визуализации множественных выравниваний последовательностей, например Jalview и UGENE .

Филогенетическое использование

Множественные выравнивания последовательностей могут быть использованы для создания филогенетического дерева . ^[52] Это стало возможным по двум причинам. Первая заключается в том, что функциональные домены, которые известны в аннотированных последовательностях, могут быть использованы для выравнивания в неаннотированных последовательностях. Другая заключается в том, что могут быть найдены консервативные области, которые, как известно, являются функционально важными. Это позволяет использовать множественные выравнивания последовательностей для анализа и поиска эволюционных связей через гомологию между последовательностями. Могут быть обнаружены точечные мутации и события вставки или удаления (называемые инделями).

Множественные выравнивания последовательностей также могут использоваться для идентификации функционально важных участков, таких как участки связывания, активные участки или участки, соответствующие другим ключевым функциям, путем поиска консервативных доменов. При рассмотрении множественных выравниваний последовательностей полезно учитывать различные аспекты последовательностей при сравнении последовательностей. Эти аспекты включают идентичность, сходство и гомологию. Идентичность означает, что последовательности имеют идентичные остатки в своих соответствующих положениях. С другой стороны, сходство связано с тем, что сравниваемые последовательности имеют схожие остатки количественно. Например, с точки зрения нуклеотидных последовательностей пиримидины считаются похожими друг на друга, как и пурины. Сходство в конечном итоге приводит к гомологии, в том смысле, что чем больше похожих последовательностей, тем ближе они к гомологичности. Это сходство в последовательностях затем может помочь найти общее происхождение. ^[52]

Смотрите также

• Анализ последовательности без выравнивания
• Кладистика
• Обобщенное выравнивание дерева
• Просмотрщики множественных выравниваний последовательностей
• PANDIT , биологическая база данных, охватывающая домены белков
• Филогенетика
• Программное обеспечение для выравнивания последовательностей
• Структурное выравнивание

Ссылки

1. Thompson JD, Linard B, Lecompte O, Poch O (2011). «Комплексное сравнительное исследование методов множественного выравнивания последовательностей: текущие проблемы и будущие перспективы». PLOS One . 6 (3): e18093. Bibcode : 2011PLoSO...618093T. doi : 10.1371/journal.pone.0018093 . PMC  3069049. PMID  21483869 .
2. Nuin PA, Wang Z, Tillier ER (2006). «Точность нескольких программ выравнивания множественных последовательностей для белков». BMC Bioinformatics . 7 : 471. doi : 10.1186/1471-2105-7-471 . PMC 1633746. PMID  17062146 . 
3. Hosseininasab A, van Hoeve WJ (2019). «Точное выравнивание множественных последовательностей с помощью синхронизированных диаграмм решений». Журнал INFORMS по вычислениям . doi : 10.1287/ijoc.2019.0937. S2CID  109937203.
4. "Помощь с матрицами, используемыми в инструментах сравнения последовательностей". Европейский институт биоинформатики. Архивировано из оригинала 11 марта 2010 г. Получено 3 марта 2010 г.
5. Ван Л., Цзян Т. (1994). «О сложности множественного выравнивания последовательностей». J Comput Biol . 1 (4): 337–348. CiteSeerX 10.1.1.408.894 . doi :10.1089/cmb.1994.1.337. PMID  8790475. 
6. Just W (2001). «Вычислительная сложность множественного выравнивания последовательностей с SP-оценкой». J Comput Biol . 8 (6): 615–23. CiteSeerX 10.1.1.31.6382 . doi :10.1089/106652701753307511. PMID  11747615. 
7. Элиас, Айзек (2006). «Урегулирование неподатливости множественного выравнивания». J Comput Biol . 13 (7): 1323–1339. CiteSeerX 10.1.1.6.256 . doi :10.1089/cmb.2006.13.1323. PMID  17037961. 
8. Каррильо Х, Липман ДЖ (1988). «Проблема выравнивания множественных последовательностей в биологии». Журнал SIAM по прикладной математике . 48 (5): 1073–1082. doi :10.1137/0148063.
9. Lipman DJ, Altschul SF, Kececioglu JD (1989). "Инструмент для множественного выравнивания последовательностей". Proc Natl Acad Sci USA . 86 (12): 4412–4415. Bibcode : 1989PNAS...86.4412L. doi : 10.1073/pnas.86.12.4412 . PMC 287279. PMID  2734293. 
10. "Программное обеспечение для генетического анализа". Национальный центр биотехнологической информации . Получено 3 марта 2010 г.
11. Feng DF, Doolittle RF (1987). «Прогрессивное выравнивание последовательностей как предпосылка для исправления филогенетических деревьев». J Mol Evol . 25 (4): 351–360. Bibcode : 1987JMolE..25..351F. doi : 10.1007/BF02603120. PMID  3118049. S2CID  6345432.
12. Mount DM. (2004). Биоинформатика: Анализ последовательностей и генома 2-е изд. Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY.
13. Хиггинс Д.Г. , Шарп П.М. (1988). «CLUSTAL: пакет для выполнения множественного выравнивания последовательностей на микрокомпьютере». Gene . 73 (1): 237–244. doi :10.1016/0378-1119(88)90330-7. PMID  3243435.
14. Томпсон Дж. Д., Хиггинс Д. Г., Гибсон Т. Дж. (ноябрь 1994 г.). «CLUSTAL W: улучшение чувствительности прогрессивного множественного выравнивания последовательностей посредством взвешивания последовательностей, штрафов за пробелы, зависящие от позиции, и выбора матрицы весов». Nucleic Acids Res . 22 (22): 4673–80. doi :10.1093/nar/22.22.4673. PMC 308517. PMID  7984417 . 
15. "EMBL-EBI-ClustalW2-Множественное выравнивание последовательностей". CLUSTALW2 .
16. Notredame C, Higgins DG, Heringa J (сентябрь 2000 г.). «T-Coffee: новый метод быстрого и точного выравнивания множественных последовательностей». J. Mol. Biol . 302 (1): 205–17. doi :10.1006/jmbi.2000.4042. PMID  10964570. S2CID  10189971.
17. Sze SH, Lu Y, Yang Q (2006). «Решаемая за полиномиальное время формулировка множественного выравнивания последовательностей». J Comput Biol . 13 (2): 309–319. doi :10.1089/cmb.2006.13.309. PMID  16597242.
18. Хиросава М., Тотоки И., Хосида М., Ишикава М. (1995). «Комплексное исследование итеративных алгоритмов множественного выравнивания последовательностей». Computer Applications in the Biosciences . 11 (1): 13–18. doi :10.1093/bioinformatics/11.1.13. PMID  7796270.
19. Гото О (1996). «Значительное улучшение точности множественных выравниваний последовательностей белков путем итеративного уточнения, оцененное по отношению к структурным выравниваниям». J Mol Biol . 264 (4): 823–38. doi :10.1006/jmbi.1996.0679. PMID  8980688.
20. Brudno M, Chapman M, Göttgens B, Batzoglou S, Morgenstern B (декабрь 2003 г.). "Быстрое и чувствительное множественное выравнивание больших геномных последовательностей". BMC Bioinformatics . 4 : 66. doi : 10.1186/1471-2105-4-66 . PMC 521198. PMID  14693042 . 
21. Эдгар RC (2004). «MUSCLE: множественное выравнивание последовательностей с высокой точностью и высокой пропускной способностью». Nucleic Acids Research . 32 (5): 1792–97. doi :10.1093/nar/gkh340. PMC 390337. PMID 15034147  . 
22. Collingridge PW, Kelly S (2012). "MergeAlign: улучшение производительности множественного выравнивания последовательностей путем динамической реконструкции консенсусных множественных выравниваний последовательностей". BMC Bioinformatics . 13 (117): 117. doi : 10.1186/1471-2105-13-117 . PMC 3413523 . PMID  22646090. 
23. Хьюи Р., Крог А. (1996). «Скрытые марковские модели для анализа последовательностей: расширение и анализ базового метода». CABIOS . 12 (2): 95–107. CiteSeerX 10.1.1.44.3365 . doi :10.1093/bioinformatics/12.2.95. PMID  8744772. 
24. Grasso C, Lee C (2004). «Объединение частичного выравнивания порядка и прогрессивного множественного выравнивания последовательностей увеличивает скорость выравнивания и масштабируемость для очень больших задач выравнивания». Биоинформатика . 20 (10): 1546–56. doi : 10.1093/bioinformatics/bth126 . PMID  14962922.
25. Хьюи Р., Крог А. SAM: Программная система выравнивания и моделирования последовательностей. Технический отчет UCSC-CRL-96-22, Калифорнийский университет, Санта-Круз, Калифорния, сентябрь 1996 г.
26. Дурбин Р., Эдди С., Крог А., Митчисон Г. (1998). Анализ биологической последовательности: вероятностные модели белков и нуклеиновых кислот, Cambridge University Press, 1998.
27. Söding J (2005). «Обнаружение гомологии белков путем сравнения HMM-HMM». Биоинформатика . 21 (7): 951–960. CiteSeerX 10.1.1.519.1257 . doi :10.1093/bioinformatics/bti125. PMID  15531603. 
28. Battey JN, Kopp J, Bordoli L, Read RJ, Clarke ND, Schwede T (2007). «Автоматизированные серверные предсказания в CASP7». Proteins . 69 (Suppl 8): 68–82. doi : 10.1002/prot.21761 . PMID  17894354. S2CID  29879391.
29. Loytynoja, A. (2005). "Алгоритм для прогрессивного множественного выравнивания последовательностей со вставками". Труды Национальной академии наук . 102 (30): 10557–10562. Bibcode : 2005PNAS..10210557L. doi : 10.1073/pnas.0409137102 . PMC 1180752. PMID  16000407 . 
30. Löytynoja A, Goldman N (июнь 2008 г.). «Размещение пробелов с учетом филогении предотвращает ошибки в выравнивании последовательностей и эволюционном анализе». Science . 320 (5883): 1632–5. Bibcode :2008Sci...320.1632L. doi :10.1126/science.1158395. PMID  18566285. S2CID  5211928.
31. Löytynoja A, Vilella AJ, Goldman N (июль 2012 г.). «Точное расширение множественных выравниваний последовательностей с использованием графового алгоритма с учетом филогении». Биоинформатика . 28 (13): 1684–91. doi :10.1093/bioinformatics/bts198. PMC 3381962. PMID  22531217 . 
32. Szalkowski AM (июнь 2012 г.). «Быстрое и надежное выравнивание множественных последовательностей с размещением пробелов с учетом филогении». BMC Bioinformatics . 13 : 129. doi : 10.1186/1471-2105-13-129 . PMC 3495709 . PMID  22694311. 
33. Henikoff S, Henikoff JG (декабрь 1991 г.). «Автоматизированная сборка белковых блоков для поиска в базе данных». Nucleic Acids Res . 19 (23): 6565–72. doi :10.1093/nar/19.23.6565. PMC 329220. PMID  1754394 . 
34. Бейли TL, Элкан C (1994). «Подгонка модели смеси с помощью максимизации ожидания для обнаружения мотивов в биополимерах» (PDF) . Труды Второй международной конференции по интеллектуальным системам для молекулярной биологии . Менло-Парк, Калифорния: AAAI Press. стр. 28–36.
35. Бейли TL, Грибсков М (1998). «Объединение доказательств с использованием p-значений: применение к поискам гомологии последовательностей». Биоинформатика . 14 (1): 48–54. doi : 10.1093/bioinformatics/14.1.48 . PMID  9520501.
36. Salama RA, Stekel DJ (ноябрь 2013 г.). «Ненезависимое энергетическое выравнивание множественных последовательностей улучшает прогнозирование сайтов связывания факторов транскрипции». Биоинформатика . 29 (21): 2699–704. doi : 10.1093/bioinformatics/btt463 . PMID  23990411.
37. Нотредам С., Хиггинс Д.Г. (апрель 1996 г.). «SAGA: выравнивание последовательностей с помощью генетического алгоритма». Нуклеиновые кислоты Рез . 24 (8): 1515–24. дои : 10.1093/нар/24.8.1515. ПМК 145823 . ПМИД  8628686. 
38. Нотредам С., О'Брайен Э.А., Хиггинс Д.Г. (1997). «RAGA: выравнивание последовательности РНК с помощью генетического алгоритма». Нуклеиновые кислоты Рез . 25 (22): 4570–80. дои : 10.1093/нар/25.22.4570. ПМК 147093 . ПМИД  9358168. 
39. Ким Дж., Праманик С., Чунг М.Дж. (1994). «Множественное выравнивание последовательностей с использованием имитированного отжига». Computer Applications in the Biosciences . 10 (4): 419–26. doi :10.1093/bioinformatics/10.4.419. PMID  7804875.
40. Althaus E, Caprara A, Lenhof HP, Reinert K (2006). «Алгоритм ветвления и отсечения для выравнивания множественных последовательностей». Математическое программирование . 105 (2–3): 387–425. doi :10.1007/s10107-005-0659-3. S2CID  17715172.
41. "D-Wave инициирует открытую квантовую программную среду 11 января 2017 г.". Архивировано из оригинала 8 марта 2021 г. Получено 20 января 2017 г.
42. "Ручное редактирование и корректировка MSA". Европейская лаборатория молекулярной биологии. 2007. Архивировано из оригинала 24 сентября 2015 г. Получено 7 марта 2010 г.
43. Castresana J (апрель 2000 г.). «Выбор консервативных блоков из множественных выравниваний для их использования в филогенетическом анализе». Молекулярная биология и эволюция . 17 (4): 540–52. doi : 10.1093/oxfordjournals.molbev.a026334 . PMID  10742046.
44. Löytynoja A, Milinkovitch MC (июнь 2001 г.). «SOAP, очистка множественных выравниваний от нестабильных блоков». Биоинформатика . 17 (6): 573–4. doi : 10.1093/bioinformatics/17.6.573 . PMID  11395440.
45. Poirot O, O'Toole E, Notredame C (июль 2003 г.). "Tcoffee@igs: веб-сервер для вычисления, оценки и комбинирования множественных выравниваний последовательностей". Nucleic Acids Res . 31 (13): 3503–6. doi :10.1093/nar/gkg522. PMC 168929. PMID  12824354 . 
46. Chang, JM; Di Tommaso, P; Notredame, C (июнь 2014 г.). «TCS: новая мера надежности множественного выравнивания последовательностей для оценки точности выравнивания и улучшения реконструкции филогенетического дерева». Молекулярная биология и эволюция . 31 (6): 1625–37. doi : 10.1093/molbev/msu117 . PMID  24694831.
47. Chang JM, Di Tommaso P, Lefort V, Gascuel O, Notredame C (июль 2015 г.). "TCS: веб-сервер для оценки множественного выравнивания последовательностей и филогенетической реконструкции". Nucleic Acids Res . 43 (W1): W3–6. doi :10.1093/nar/gkv310. PMC 4489230. PMID  25855806 . 
48. Брэдли РК, Робертс А, Смут М, Ювекар С, До Дж, Дьюи К, Холмс И, Пахтер Л (май 2009 г.). "Быстрое статистическое выравнивание". PLOS Comput. Biol . 5 (5): e1000392. Bibcode : 2009PLSCB...5E0392B. doi : 10.1371/journal.pcbi.1000392 . PMC 2684580. PMID  19478997 . 
49. Ландан Г., Граур Д. (2008). «Меры локальной надежности из наборов кооптимальных множественных выравниваний последовательностей». Биокомпьютинг 2008. С. 15–24. doi :10.1142/9789812776136_0003. ISBN 978-981-277-608-2. PMID  18229673. {{cite book}}: |journal=проигнорировано ( помощь )
50. Penn O, Privman E, Landan G, Graur D, Pupko T (август 2010 г.). «Оценка достоверности выравнивания, фиксирующая надежность для управления неопределенностью дерева». Молекулярная биология и эволюция . 27 (8): 1759–67. doi :10.1093/molbev/msq066. PMC 2908709. PMID  20207713 . 
51. Redelings BD, Suchard MA (июнь 2005 г.). «Совместная байесовская оценка выравнивания и филогении». Syst. Biol . 54 (3): 401–18. doi : 10.1080/10635150590947041 . PMID  16012107.
52. Budd, Aidan (10 февраля 2009 г.). "Упражнения и демонстрации множественного выравнивания последовательностей". Европейская лаборатория молекулярной биологии. Архивировано из оригинала 5 марта 2012 г. Получено 30 июня 2010 г.

Обзорные статьи

• Дюре, Л.; С. Абдеддайм (2000). «Множественное выравнивание для структурно-функционального или филогенетического анализа гомологичных последовательностей». В D. Higgins и W. Taylor (ред.). Структура последовательности биоинформатики и банки данных . Оксфорд: Oxford University Press.
• Notredame, C. (2002). «Недавние достижения в выравнивании множественных последовательностей: обзор». Фармакогеномика . 3 (1): 131–144. doi :10.1517/14622416.3.1.131. PMID  11966409.
• Томпсон, Дж. Д.; Плевняк, Ф.; Поч, О. (1999). «Комплексное сравнение программ выравнивания множественных последовательностей». Nucleic Acids Research . 27 (13): 12682–2690. doi :10.1093/nar/27.13.2682. PMC  148477. PMID  10373585 .
• Уоллес, IM; Блэкшилдс, G.; Хиггинс, DG (2005). «Множественные выравнивания последовательностей». Curr Opin Struct Biol . 15 (3): 261–266. doi :10.1016/j.sbi.2005.04.002. PMID  15963889.
• Notredame, C (2007). "Современные разработки алгоритмов выравнивания множественных последовательностей". PLOS Computational Biology . 3 (8): e123. Bibcode : 2007PLSCB...3..123N. doi : 10.1371/journal.pcbi.0030123 . PMC  1963500. PMID  17784778 .

Внешние ссылки

• Инструменты выравнивания последовательностей ExPASy
• Архивированная страница ресурсов по множественному выравниванию – из Виртуальной школы естественных наук
• Инструменты для множественного выравнивания – от Pôle Bioinformatique Lyonnais
• Точка входа к кластерным серверам и информации
• Точка входа к основным серверам T-Coffee
• Точка входа на главный сервер MergeAlign и информацию
• Серверы Европейского института биоинформатики:
  • ClustalW2 – универсальная программа выравнивания множественных последовательностей ДНК или белков.
  • Мышцы – Сравнение множественных последовательностей с помощью логарифмического ожидания
  • T-кофе – множественное выравнивание последовательностей.
  • MAFFT – множественное выравнивание с использованием быстрого преобразования Фурье
  • KALIGN – быстрый и точный алгоритм множественного выравнивания последовательностей.

Конспекты лекций, учебные пособия и курсы

• Лекции по множественному выравниванию последовательностей — от Института молекулярной генетики Общества Макса Планка
• Конспект лекций и практические занятия по множественным выравниваниям последовательностей в Европейской лаборатории молекулярной биологии (EMBL)
• Конспект лекций по молекулярной биоинформатике
• Конспект лекций по молекулярной эволюции и биоинформатике