Модели грунтовых вод — это компьютерные модели систем потока грунтовых вод , которые используются гидрологами и гидрогеологами . Модели грунтовых вод используются для моделирования и прогнозирования условий водоносных горизонтов .

Однозначное определение понятия «модель подземных вод» дать сложно, но существует много общих характеристик.
Модель грунтовых вод может быть масштабной моделью или электрической моделью ситуации с грунтовыми водами или водоносным слоем . Модели грунтовых вод используются для представления естественного потока грунтовых вод в окружающей среде. Некоторые модели грунтовых вод включают (химические) аспекты качества грунтовых вод. Такие модели грунтовых вод пытаются предсказать судьбу и движение химиката в естественном, городском или гипотетическом сценарии.
Модели грунтовых вод могут использоваться для прогнозирования последствий гидрологических изменений (например, откачки грунтовых вод или развития орошения) на поведение водоносного горизонта и часто называются моделями имитации грунтовых вод. Модели грунтовых вод используются в различных планах управления водными ресурсами для городских территорий.
Поскольку вычисления в математических моделях подземных вод основаны на уравнениях потока подземных вод , которые являются дифференциальными уравнениями , которые часто можно решить только приближенными методами с использованием численного анализа , эти модели также называются математическими, числовыми или вычислительными моделями подземных вод . [1]
Математические или численные модели обычно основаны на реальной физике, которой следует поток грунтовых вод. Эти математические уравнения решаются с использованием численных кодов, таких как MODFLOW , ParFlow, HydroGeoSphere , OpenGeoSys и т. д. Различные типы численных решений , такие как метод конечных разностей и метод конечных элементов, обсуждаются в статье « Гидрогеология ».
Для расчетов необходимы такие входные данные, как:
Модель может включать химические компоненты, такие как соленость воды , соленость почвы и другие показатели качества воды и почвы, для которых также могут потребоваться входные данные.

Первичной связью между грунтовыми водами и гидрологическими входами является ненасыщенная зона или зона аэрации . Почва действует для разделения гидрологических входов, таких как осадки или таяние снега, на поверхностный сток , влажность почвы , эвапотранспирацию и пополнение грунтовых вод . Потоки через ненасыщенную зону , которые связывают поверхностные воды с влажностью почвы и грунтовыми водами , могут быть восходящими или нисходящими, в зависимости от градиента гидравлического напора в почве, можно моделировать с помощью численного решения уравнения Ричардса [2], уравнения в частных производных или обыкновенного дифференциального уравнения, метода конечного содержания воды [3], как это было проверено для моделирования взаимодействий грунтовых вод и зоны аэрации . [4]
Эксплуатационные входы касаются вмешательства человека в управление водными ресурсами, например , орошение , дренаж , откачка из скважин , контроль уровня грунтовых вод и эксплуатация удерживающих или инфильтрационных бассейнов, которые часто имеют гидрологическую природу.
Эти входы также могут меняться во времени и пространстве.
Множество моделей подземных вод создаются с целью оценки воздействия гидротехнических мероприятий.

Граничные условия могут быть связаны с уровнями грунтовых вод , артезианскими давлениями и гидравлическим напором вдоль границ модели с одной стороны ( условия напора ), или с притоками и оттоками грунтовых вод вдоль границ модели с другой стороны ( условия потока ). Это может также включать качественные аспекты воды, такие как соленость.
Начальные условия относятся к начальным значениям элементов, которые могут увеличиваться или уменьшаться с течением времени внутри области модели, и они охватывают в основном те же явления, что и граничные условия.
Начальные и граничные условия могут меняться от места к месту. Граничные условия могут быть как постоянными, так и меняться во времени.
.JPG/440px-File-Saltmod8_(2).JPG)
Параметры обычно касаются геометрии и расстояний в моделируемой области, а также тех физических свойств водоносного горизонта, которые более или менее постоянны во времени, но могут изменяться в пространстве.
Важными параметрами являются рельеф , толщина слоев почвы/горной породы и их горизонтальная/вертикальная гидравлическая проводимость (проницаемость для воды), водопроницаемость и сопротивление водоносного горизонта , пористость и коэффициент хранения водоносного горизонта , а также капиллярность ненасыщенной зоны. Более подробную информацию см. в статье о гидрогеологии .
Некоторые параметры могут зависеть от изменений в состоянии грунтовых вод, например, толщина слоя почвы, которая может уменьшаться при падении уровня грунтовых вод и/или снижении гидравлического давления. Это явление называется просадкой . Толщина в этом случае является переменной во времени и не является параметром в собственном смысле.
Применимость модели грунтовых вод к реальной ситуации зависит от точности входных данных и параметров . Определение их требует значительного изучения, например, сбора гидрологических данных ( осадки , эвапотранспирация , орошение , дренаж ) и определения упомянутых выше параметров, включая испытания на откачку . Поскольку многие параметры довольно изменчивы в пространстве, для получения репрезентативных значений необходима экспертная оценка.
Модели также могут быть использованы для анализа «если-тогда» : если значение параметра равно A, то каков результат, а если значение параметра равно B, то каково влияние? Этот анализ может быть достаточным для получения приблизительного впечатления о поведении грунтовых вод, но он также может служить для проведения анализа чувствительности , чтобы ответить на вопрос: какие факторы оказывают большое влияние, а какие — меньшее. Имея такую информацию, можно направить усилия исследования больше на влиятельные факторы.
Когда собрано достаточно данных, можно определить часть недостающей информации с помощью калибровки . Это подразумевает, что предполагается диапазон значений для неизвестного или сомнительного значения определенного параметра, и модель многократно запускается, сравнивая результаты с известными соответствующими данными. Например, если имеются данные о солености грунтовых вод, а значение гидравлической проводимости неопределенно, предполагается диапазон проводимостей и выбирается то значение проводимости как «истинное», которое дает результаты солености, близкие к наблюдаемым значениям, что означает, что поток грунтовых вод, регулируемый гидравлической проводимостью, согласуется с условиями солености. Эта процедура похожа на измерение потока в реке или канале, когда очень соленая вода с известной концентрацией соли капает в канал и измеряется полученная концентрация соли ниже по течению.
Модели подземных вод могут быть одномерными, двумерными, трехмерными и полутрехмерными. Двухмерные и трехмерные модели могут учитывать анизотропию водоносного горизонта по отношению к гидравлической проводимости , т.е. это свойство может изменяться в разных направлениях.

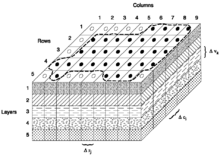

В полутрехмерных моделях горизонтальный поток описывается двумерными уравнениями потока (т.е. в горизонтальном направлении x и y). Вертикальные потоки (в направлении z) описываются (a) одномерным уравнением потока или (b) выводятся из водного баланса горизонтальных потоков, преобразуя избыток горизонтально входящих над горизонтально исходящими грунтовыми водами в вертикальный поток в предположении, что вода несжимаема .
Существует два класса полутрехмерных моделей:
Примером недискретизированной радиальной модели является описание потока грунтовых вод, движущегося радиально к глубокой скважине в сети скважин, из которых извлекается вода. [7] Радиальный поток проходит через вертикальное цилиндрическое поперечное сечение, представляющее гидравлический эквипотенциал , поверхность которого уменьшается в направлении оси пересечения радиальных плоскостей, где расположена скважина.

Призматически дискретизированные модели, такие как SahysMod [8], имеют сетку только над поверхностью земли. Двумерная сетка состоит из треугольников, квадратов, прямоугольников или многоугольников . Следовательно, область потока подразделяется на вертикальные блоки или призмы . Призмы могут быть дискретизированы на горизонтальные слои с различными характеристиками, которые также могут различаться между призмами. Поток грунтовых вод между соседними призмами рассчитывается с использованием двумерных уравнений горизонтального потока грунтовых вод. Вертикальные потоки находятся путем применения одномерных уравнений потока в вертикальном смысле, или они могут быть выведены из водного баланса: избыток горизонтального притока над горизонтальным оттоком (или наоборот) преобразуется в вертикальный поток, как показано в статье Гидрология (сельское хозяйство) .
В полутрехмерных моделях промежуточный поток между горизонтальным и вертикальным не моделируется как в настоящих трехмерных моделях. Однако, как и настоящие трехмерные модели, такие модели позволяют вводить горизонтальные и вертикальные подземные дренажные системы.
Полузамкнутые водоносные горизонты с медленно проницаемым слоем, залегающим над водоносным горизонтом ( водоупором ), могут быть включены в модель путем моделирования вертикального потока через него под воздействием избыточного давления в самом водоносном горизонте относительно уровня грунтовых вод внутри или над водоупором.