Рассечение на ортосхемы

Нерешенная задача по математике :

Можно ли любой симплекс разбить на ограниченное число ортосхем?

(еще нерешенные задачи по математике)

В геометрии это нерешенная гипотеза Хьюго Хадвигера о том, что каждый симплекс можно разбить на ортосхемы , используя количество ортосхем, ограниченное функцией размерности симплекса. ^[1] Если это правда, то в более общем смысле каждый выпуклый многогранник можно разбить на ортосхемы.

Определения и заявление

В этом контексте симплекс в -мерном евклидовом пространстве — это выпуклая оболочка точек , которые не все лежат в общей гиперплоскости . Например, 2-мерный симплекс — это просто треугольник (выпуклая оболочка из трех точек на плоскости), а 3-мерный симплекс — это тетраэдр ( выпуклая оболочка из четырех точек в трехмерном пространстве). Точки, образующие таким образом симплекс, называются его вершинами . ${\displaystyle d}$ ${\displaystyle d+1}$

Ортосхема, также называемая симплексом путей, представляет собой особый вид симплекса. В нем вершины могут быть соединены путем так , что каждые два ребра пути расположены под прямым углом друг к другу. Двумерная ортосхема представляет собой прямоугольный треугольник . Трехмерную ортосхему можно построить из куба , найдя путь из трех ребер куба, которые не все лежат на одной квадратной грани, и образовав выпуклую оболочку из четырех вершин на этом пути.

Разложение куба на шесть ортосхем.

Рассечение фигуры (которой может быть любое замкнутое множество в евклидовом пространстве) — это представление как объединения других фигур, внутренности которых не пересекаются друг с другом . То есть интуитивно фигуры в объединении не перекрываются, хотя на своих границах могут иметь общие точки. Например, куб можно разбить на шесть трехмерных ортосхем. Похожий результат применим и в более общем плане: любой гиперкуб или гиперпрямоугольник в измерениях можно разбить на ортосхемы. ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle d}$ ${\displaystyle d!}$

Гипотеза Хадвигера состоит в том, что существует функция , по которой любой -мерный симплекс можно разбить не более чем на ортосхемы. Хадвигер поставил эту проблему в 1956 году; ^{В [2]} она в целом остается нерешенной, хотя известны частные случаи при малых значениях . ^[1] ${\displaystyle f}$ ${\displaystyle d}$ ${\displaystyle f(d)}$ ${\displaystyle d}$

В небольших размерах

Высота под острым углом может не рассечь треугольник, но высота под самым широким углом всегда рассекает его на два прямоугольных треугольника.

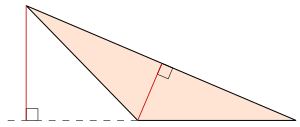
В двух измерениях каждый треугольник можно разрезать не более чем на два прямоугольных треугольника, опустив высоту от самого широкого угла к самому длинному краю. ^[2]

В трех измерениях некоторые тетраэдры можно разрезать аналогичным образом, опуская высоту перпендикулярно от вершины до точки на противоположной грани, соединяясь перпендикулярно со сторонами грани и используя трехреберные перпендикулярные пути через и к сторону, а затем к вершине лица. ^[2] Однако это не всегда работает. В частности, существуют тетраэдры, у которых ни одна из вершин не имеет высоты со ногой внутри противоположной грани. Используя более сложную конструкцию, Ленхард (1960) доказал, что каждый тетраэдр можно разбить не более чем на 12 ортосхем. ^[3] Бём (1980) доказал, что это оптимально: существуют тетраэдры, которые нельзя разбить менее чем на 12 ортосхем. ^[4] В той же статье Бём также обобщил результат Ленхарда на трёхмерную сферическую геометрию и трёхмерную гиперболическую геометрию . ${\displaystyle v}$ ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle v}$ ${\displaystyle p}$

В четырех измерениях необходимо не более 500 ортосхем. ^[5] В пяти измерениях снова необходимо конечное число ортосхем, примерно не более 12,5 миллионов. Опять же, это относится к сферической геометрии и гиперболической геометрии, а также к евклидовой геометрии. ^[6]

Гипотеза Хадвигера остается недоказанной для всех размерностей больше пяти. ^[1]

Последствия

Любой выпуклый многогранник можно разбить на симплексы. Следовательно, если гипотеза Хадвигера верна, каждый выпуклый многогранник также будет расщепляться на ортосхемы. ^[6]

Связанный с этим результат состоит в том, что каждая ортосхема сама по себе может быть разделена на ортосхемы или более мелкие. ^{[7] [8]} Следовательно, для симплексов, которые можно разбить на ортосхемы, их разрезы могут иметь сколь угодно большое количество ортосхем. ${\displaystyle d}$ ${\displaystyle d+1}$

Рекомендации

1. Брандтс, Ян; Коротов Сергей; Кржижек, Михал; Шольц, Якуб (2009), «О нетупых симплициальных разбиениях» (PDF) , SIAM Review , 51 (2): 317–335, doi : 10.1137/060669073, MR  2505583. См., в частности, гипотезу 23, с. 327.
2. Хадвигер, Хьюго (1956), «Ungelöste Issuee», Elemente der Mathematik , 11 : 109–110
3. Ленхард, Х.-Хр. (1960), «Zerlegung von Tetraedern в ортогональном тетраэдере», Elemente der Mathematik , 15 : 106–107, MR  0116226
4. Бём, Йоханнес (1980), "Zur vollständigen Zerlegung der euklidischen und nichteuklidischen Tetraeder in Orthogonal-Tetraeder", Мартин-Лютер-Университет Галле-Виттенберг (9): 29–54, MR  0579516
5. Чирпке, Катрин (1993), «О расчленении симплексов на ортосхемы», Geometriae Dedicata , 46 (3): 313–329, doi : 10.1007/BF01263622, MR  1220122
6. Tschirpke, Katrin (1994), «Разделение пятимерных симплексов на ортосхемы», Beiträge zur Algebra und Geometry , 35 (1): 1–11, MR  1287191
7. Дебруннер, Ганс Э. (1990), «Разделение ортосхем на ортосхемы», Geometriae Dedicata , 33 (2): 123–152, doi : 10.1007/BF00183080, MR  1050606
8. Брандтс, Ян; Коротов Сергей; Кржижек, Михал (2007), «Расчленение пути-симплекса на пути -подсимплексы», Линейная алгебра и ее приложения , 421 (2–3): 382–393, doi : 10.1016/j.laa.2006.10.010 , МР  2294350 ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle n}$