Набор данных по цветкам ириса или набор данных по ирису Фишера — это многомерный набор данных , который использовал и прославил британский статистик и биолог Рональд Фишер в своей статье 1936 года « Использование множественных измерений в таксономических задачах» в качестве примера линейного дискриминантного анализа . [1] Иногда его называют набором данных по ирису Андерсона , поскольку Эдгар Андерсон собрал данные для количественной оценки морфологических вариаций цветков ириса трех родственных видов. [2] Два из трех видов были собраны на полуострове Гаспе «все с одного пастбища, собраны в один день и измерены в одно и то же время одним и тем же человеком с помощью одного и того же прибора». [3]
Набор данных состоит из 50 образцов каждого из трех видов ириса ( Iris setosa , Iris virginica и Iris versicolor ). Четыре характеристики были измерены для каждого образца: длина и ширина чашелистиков и лепестков в сантиметрах. На основе комбинации этих четырех характеристик Фишер разработал линейную дискриминантную модель для различения каждого вида. Статья Фишера была опубликована в Annals of Eugenics (сегодня Annals of Human Genetics ). [1]


Первоначально он использовался в качестве примера набора данных, к которому был применен линейный дискриминантный анализ Фишера , но впоследствии стал типичным тестовым случаем для многих статистических методов классификации в машинном обучении, таких как машины опорных векторов . [5]
Однако использование этого набора данных в кластерном анализе не является обычным, поскольку набор данных содержит только два кластера с довольно очевидным разделением. Один из кластеров содержит Iris setosa , в то время как другой кластер содержит как Iris virginica , так и Iris versicolor и не может быть разделен без информации о виде, которую использовал Фишер. Это делает набор данных хорошим примером для объяснения разницы между контролируемыми и неконтролируемыми методами в добыче данных : линейная дискриминантная модель Фишера может быть получена только тогда, когда известны виды объектов: метки классов и кластеры не обязательно совпадают. [6]
Тем не менее, все три вида Iris разделимы в проекции на нелинейный и ветвящийся главный компонент. [7] Набор данных аппроксимируется ближайшим деревом с некоторым штрафом за чрезмерное количество узлов, изгибы и растяжения. Затем строится так называемая «карта метро». [4] Точки данных проецируются в ближайший узел. Для каждого узла подготавливается круговая диаграмма проецируемых точек. Площадь круговой диаграммы пропорциональна количеству проецируемых точек. Из диаграммы (слева) ясно, что абсолютное большинство образцов различных видов Iris принадлежат к разным узлам. Только небольшая часть Iris-virginica смешана с Iris-versicolor (смешанные сине-зеленые узлы на диаграмме). Таким образом, три вида Iris ( Iris setosa , Iris virginica и Iris versicolor ) разделимы неконтролируемыми процедурами нелинейного анализа главных компонент . Чтобы различить их, достаточно просто выбрать соответствующие узлы на главном дереве.

Набор данных содержит 150 записей по пяти атрибутам: длина чашелистика, ширина чашелистика, длина лепестка, ширина лепестка и вид.


Набор данных iris широко используется в качестве набора данных для начинающих в целях машинного обучения. Набор данных включен в R base и Python в библиотеку машинного обучения scikit-learn , так что пользователи могут получить к нему доступ без необходимости искать его источник.
Было опубликовано несколько версий набора данных. [8]
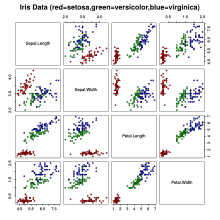
Приведенный ниже пример кода R воспроизводит диаграмму рассеяния, представленную в верхней части этой статьи:
# Показать набор данных iris # Показать страницу справки с информацией о наборе данных ? iris# Создать диаграммы рассеяния всех парных комбинаций 4 переменных в наборе данных pairs ( iris [ 1 : 4 ], main = "Iris Data (red=setosa,green=versicolor,blue=virginica)" , pch = 21 , bg = c ( "red" , "green3" , "blue" )[ unclass ( iris $ Species )]) из sklearn.datasets импортировать load_irisирис = load_iris () ирисЭтот код дает:
{ 'data' : array ([[ 5.1 , 3.5 , 1.4 , 0.2 ], [ 4.9 , 3. , 1.4 , 0.2 ], [ 4.7 , 3.2 , 1.3 , 0.2 ], [ 4.6 , 3.1 , 1.5 , 0.2 ], ... 'target' : array ([ 0 , 0 , 0 , ... 1 , 1 , 1 , ... 2 , 2 , 2 , ... 'target_names' : array ([ 'setosa' , 'versicolor' , 'virginica' ], dtype = '<U10' ), ... }