В формальной теории языка контекстно-свободная грамматика G называется находящейся в нормальной форме Хомского (впервые описанной Ноамом Хомским ) [1], если все ее правила вывода имеют вид: [2] [3]
где A , B и C — нетерминальные символы , буква a — терминальный символ (символ, представляющий постоянное значение), S — начальный символ, а ε обозначает пустую строку . Кроме того, ни B , ни C не могут быть начальным символом , а третье правило производства может появиться только в том случае, если ε находится в L ( G ), языке , созданном контекстно-свободной грамматикой G. [4] : 92–93, 106
Каждая грамматика в нормальной форме Хомского является контекстно-свободной, и наоборот, каждая контекстно-свободная грамматика может быть преобразована в эквивалентную грамматику [примечание 1] , которая находится в нормальной форме Хомского и имеет размер, не превышающий квадрат размера исходной грамматики.
Чтобы преобразовать грамматику в нормальную форму Хомского, применяется последовательность простых преобразований в определенном порядке; это описано в большинстве учебников по теории автоматов . [4] : 87–94 [5] [6] [7] Представленное здесь изложение следует Хопкрофту, Ульману (1979), но адаптировано для использования названий преобразований из Ланге, Лейсса (2009). [8] [примечание 2] Каждое из следующих преобразований устанавливает одно из свойств, требуемых для нормальной формы Хомского.
Ввести новый начальный символ S 0 и новое правило
где S — предыдущий начальный символ. Это не меняет язык, создаваемый грамматикой, и S 0 не будет встречаться в правой части любого правила.
Чтобы устранить каждое правило
с терминальным символом a, не являющимся единственным символом в правой части, ввести для каждого такого терминала новый нетерминальный символ N a и новое правило
Изменить все правила
к
Если несколько терминальных символов встречаются с правой стороны, одновременно замените каждый из них связанным с ним нетерминальным символом. Это не изменит язык, созданный грамматикой. [4] : 92
Заменить каждое правило
с более чем 2 нетерминалами X 1 ,..., X n по правилам
где A i — новые нетерминальные символы. Опять же, это не меняет язык, созданный грамматикой. [4] : 93
ε-правило — это правило вида
где A не является S 0 , начальным символом грамматики.
Чтобы исключить все правила этой формы, сначала определите множество всех нетерминалов, которые выводят ε. Хопкрофт и Ульман (1979) называют такие нетерминалы nullable и вычисляют их следующим образом:
Получите промежуточную грамматику, заменив каждое правило
всеми версиями с некоторыми пропущенными обнуляемыми X i . Удаляя в этой грамматике каждое ε-правило, если только его левая часть не является начальным символом, получаем преобразованную грамматику. [4] : 90
Например, в следующей грамматике с начальным символом S 0 ,
нетерминал A , а значит и B , допускает значение null, тогда как ни C , ни S 0 не допускают. Следовательно, получается следующая промежуточная грамматика: [примечание 3]
В этой грамматике все ε-правила были « встроены в место вызова». [примечание 4] На следующем этапе их можно удалить, получив следующую грамматику:
Эта грамматика создает тот же язык, что и исходный пример грамматики, а именно. { ab , aba , abaa , abab , abac , abb , abc , b , ba , baa , bab , bac , bb , bc , c }, но не имеет ε-правил.
Правило единицы — это правило вида
где A , B — нетерминальные символы. Чтобы удалить его, для каждого правила
где X 1 ... X n — строка нетерминалов и терминалов, добавьте правило
Если только это не правило единицы, которое уже было (или удаляется). Пропуск нетерминального символа B в результирующей грамматике возможен из-за того, что B является членом замыкания единицы нетерминального символа A . [9]
При выборе порядка, в котором должны применяться вышеуказанные преобразования, следует учитывать, что некоторые преобразования могут разрушить результат, достигнутый другими. Например, START повторно введет правило единицы, если оно применяется после UNIT . Таблица показывает, какие упорядочения допускаются.
Более того, наихудшее увеличение размера грамматики [примечание 5] зависит от порядка преобразования. Используя | G | для обозначения размера исходной грамматики G , увеличение размера в наихудшем случае может варьироваться от | G | 2 до 2 2 |G| , в зависимости от используемого алгоритма преобразования. [8] : 7 Увеличение размера грамматики зависит от порядка между DEL и BIN . Оно может быть экспоненциальным, когда DEL выполняется первым, но линейным в противном случае. UNIT может повлечь за собой квадратичное увеличение размера грамматики. [8] : 5 Упорядочения START , TERM , BIN , DEL , UNIT и START , BIN , DEL , UNIT , TERM приводят к наименьшему (т. е. квадратичному) увеличению.
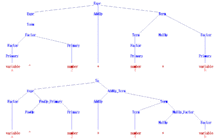
Следующая грамматика с начальным символом Expr описывает упрощенную версию множества всех синтаксически допустимых арифметических выражений в языках программирования, таких как C или Algol60 . И число, и переменная считаются здесь терминальными символами для простоты, поскольку в компиляторе front-end их внутренняя структура обычно не рассматривается синтаксическим анализатором . Терминальный символ "^" обозначает возведение в степень в Algol60.
На шаге "START" вышеприведенного алгоритма преобразования в грамматику добавляется только правило S 0 → Expr . После шага "TERM" грамматика выглядит так:
После шага «BIN» получается следующая грамматика:
Поскольку ε-правил нет, шаг "DEL" не меняет грамматику. После шага "UNIT" получается следующая грамматика, которая находится в нормальной форме Хомского:
N a , представленные на шаге "TERM", — это PowOp , Open и Close . A i , представленные на шаге "BIN", — это AddOp_Term , MulOp_Factor , PowOp_Primary и Expr_Close .
Другой способ [4] : 92 [10] определить нормальную форму Хомского:
Формальная грамматика находится в редуцированной форме Хомского , если все ее правила производства имеют вид:
где , и являются нетерминальными символами, а является терминальным символом . При использовании этого определения или может быть начальным символом. Только те контекстно-свободные грамматики, которые не генерируют пустую строку, могут быть преобразованы в приведенную форму Хомского.
В письме, где он предложил термин форма Бэкуса–Наура (БНФ), Дональд Э. Кнут подразумевал БНФ, «синтаксис, в котором все определения имеют такую форму, что можно сказать, что он находится в «нормальной форме Флойда»»,
где , и являются нетерминальными символами, а является терминальным символом, поскольку Роберт У. Флойд в 1961 году обнаружил, что любой синтаксис BNF может быть преобразован в указанный выше. [11] Но он отозвал этот термин, «поскольку, несомненно, многие люди независимо использовали этот простой факт в своих собственных работах, и этот момент лишь второстепенный по отношению к основным соображениям заметки Флойда». [12] В то время как в заметке Флойда цитируется оригинальная статья Хомского 1959 года, в письме Кнута этого нет.
Помимо своего теоретического значения, преобразование CNF используется в некоторых алгоритмах в качестве этапа предварительной обработки, например, в алгоритме CYK , восходящем синтаксическом анализе для контекстно-свободных грамматик, и его вероятностном варианте CKY. [13]
{{cite book}}: CS1 maint: числовые имена: список авторов ( ссылка ) (страницы 171-183 раздела 7.1: Нормальная форма Хомского)