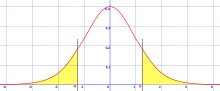
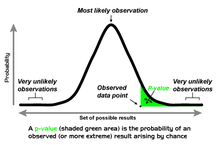
В статистической значимости односторонний тест и двусторонний тест являются альтернативными способами вычисления статистической значимости параметра, выведенного из набора данных, в терминах статистики теста . Двусторонний тест подходит, если оценочное значение больше или меньше определенного диапазона значений, например, может ли испытуемый набрать баллы выше или ниже определенного диапазона. Этот метод используется для проверки нулевой гипотезы , и если оценочное значение существует в критических областях, альтернативная гипотеза принимается вместо нулевой гипотезы. Односторонний тест подходит, если оценочное значение может отклоняться от контрольного значения только в одном направлении, влево или вправо, но не в обоих. Примером может служить, производит ли машина более одного процента дефектной продукции. В этой ситуации, если оценочное значение существует в одной из односторонних критических областей, в зависимости от направления интереса (больше или меньше), альтернативная гипотеза принимается вместо нулевой гипотезы. Альтернативные названия — односторонние и двусторонние тесты; Термин «хвост» используется потому, что крайние части распределений, где наблюдения приводят к отклонению нулевой гипотезы, малы и часто «сворачиваются» к нулю, как в нормальном распределении , окрашенном в желтый цвет, или «колоколообразной кривой», изображенной справа и окрашенной в зеленый цвет.
Односторонние тесты используются для асимметричных распределений, которые имеют один хвост, например, распределение хи-квадрат , которое часто используется при измерении степени соответствия , или для одной стороны распределения, которая имеет два хвоста, например, нормальное распределение , которое часто используется при оценке местоположения; это соответствует указанию направления. Двусторонние тесты применимы только при наличии двух хвостов, например, в нормальном распределении, и соответствуют рассмотрению любого направления как значимого. [1] [2]
В подходе Рональда Фишера нулевая гипотеза H 0 будет отклонена, когда p -значение тестовой статистики достаточно экстремально (по сравнению с распределением выборки тестовой статистики ) и, таким образом, считается маловероятным, что является результатом случайности. Обычно это делается путем сравнения полученного p -значения с указанным уровнем значимости, обозначенным как , при вычислении статистической значимости параметра . В одностороннем тесте «экстремальное» определяется заранее как «достаточно малое» или «достаточно большое» — значения в другом направлении считаются незначимыми. Можно сообщить, что вероятность левого или правого хвоста является односторонним p -значением, которое в конечном итоге соответствует направлению, в котором тестовая статистика отклоняется от H 0. [3] В двустороннем тесте «экстремальное» означает «либо достаточно малое, либо достаточно большое», и значения в любом направлении считаются значимыми. [4] Для данной тестовой статистики существует один двухсторонний тест и два односторонних теста, по одному для каждого направления. При предоставлении уровня значимости критические области будут существовать на двух концах хвоста распределения с площадью каждого для двухстороннего теста. В качестве альтернативы критическая область будет существовать только на одном конце хвоста с площадью для одностороннего теста. Для данного уровня значимости в двухстороннем тесте для тестовой статистики соответствующие односторонние тесты для той же тестовой статистики будут считаться либо вдвое более значимыми (половина p -значения), если данные находятся в направлении, указанном тестом, либо вообще не значимыми ( p -значение выше ), если данные находятся в направлении, противоположном критической области, указанной тестом.
Например, если подбрасывать монету, проверка того, смещена ли она в сторону орла, является односторонним тестом, и получение данных «всех орлов» будет рассматриваться как высокозначимый, в то время как получение данных «всех решек» будет вообще незначимым ( p = 1). Напротив, проверка того, смещена ли она в любом направлении, является двусторонним тестом, и либо «все орлы», либо «все решки» будут рассматриваться как высокозначимые данные. В медицинском тестировании, в то время как обычно интересуются, приводит ли лечение к результатам, которые лучше случайности, таким образом предполагая односторонний тест; худший результат также интересен для научной области, поэтому следует использовать двусторонний тест, который соответствует вместо этого проверке того, приводит ли лечение к результатам, которые отличаются от случайности, либо лучше, либо хуже. [5] В архетипическом эксперименте с леди, дегустирующей чай , Фишер проверял, была ли рассматриваемая леди лучше случайности в различении двух типов приготовления чая, а не то, отличалась ли ее способность от случайности, и поэтому он использовал односторонний тест.
При подбрасывании монеты нулевая гипотеза представляет собой последовательность испытаний Бернулли с вероятностью 0,5, дающую случайную величину X, которая равна 1 для орла и 0 для решки, а общая статистика теста — это выборочное среднее (количества орлов). Если проверяется, смещена ли монета в сторону орла, будет использоваться односторонний тест — только большое количество орлов будет иметь значение. В этом случае набор данных из пяти орлов (HHHHH) со средним значением выборки 1 имеет вероятность появления (5 последовательных подбрасываний с 2 исходами - ((1/2)^5 =1/32). Это имело бы и было бы значимым (отвергая нулевую гипотезу), если бы тест анализировался на уровне значимости (уровень значимости, соответствующий границе отсечения). Однако, если бы проверялось, смещена ли монета в сторону орла или решки, использовался бы двухсторонний тест, и набор данных из пяти орлов (среднее значение выборки 1) был бы таким же экстремальным, как и набор данных из пяти решек (среднее значение выборки 0). В результате p -значение было бы и это не было бы значимым (не отвергая нулевую гипотезу), если бы тест анализировался на уровне значимости .

Значение p было введено Карлом Пирсоном [6] в критерий хи-квадрат Пирсона , где он определил P (исходная запись) как вероятность того, что статистика будет на заданном уровне или выше. Это одностороннее определение, а распределение хи-квадрат асимметрично, допуская только положительные или нулевые значения, и имеет только один хвост, верхний. Оно измеряет качество соответствия данных теоретическому распределению, причем ноль соответствует точному соответствию теоретическому распределению; значение p , таким образом, измеряет, насколько вероятно, что соответствие будет настолько плохим или еще хуже.

Различие между односторонними и двусторонними тестами было популяризировано Рональдом Фишером в влиятельной книге «Статистические методы для научных работников » [7] , где он применил его, в частности, к нормальному распределению , которое является симметричным распределением с двумя равными хвостами. Нормальное распределение является общей мерой местоположения, а не качества соответствия, и имеет два хвоста, соответствующих оценке местоположения выше или ниже теоретического местоположения (например, выборочное среднее по сравнению с теоретическим средним). В случае симметричного распределения, такого как нормальное распределение, одностороннее p -значение составляет ровно половину двухстороннего p -значения: [7]
Некоторую путаницу иногда вносит тот факт, что в некоторых случаях мы хотим знать вероятность того, что отклонение, которое известно как положительное, превысит наблюдаемое значение, тогда как в других случаях требуется вероятность того, что отклонение, которое одинаково часто бывает положительным и отрицательным, превысит наблюдаемое значение; последняя вероятность всегда вдвое меньше первой.
Фишер подчеркивал важность измерения хвоста — наблюдаемого значения тестовой статистики и всех более экстремальных — а не просто вероятности конкретного результата как такового в своей работе «Планирование экспериментов» (1935). [8] Он объясняет это тем, что конкретный набор данных может быть маловероятным (в нулевой гипотезе), но более экстремальные результаты вероятны, поэтому, если рассматривать это в свете, конкретные, но не крайне маловероятные данные не следует считать значимыми.
Если тестовая статистика следует распределению Стьюдента t в нулевой гипотезе (что часто встречается, когда базовая переменная следует нормальному распределению с неизвестным масштабным коэффициентом), то тест называется односторонним или двусторонним t -тестом . Если тест выполняется с использованием фактического среднего значения и дисперсии совокупности, а не оценки по выборке, его называют односторонним или двусторонним Z -тестом .
Статистические таблицы для t и для Z предоставляют критические значения как для односторонних, так и для двусторонних тестов. То есть, они предоставляют критические значения, которые отсекают целую область на одном или другом конце выборочного распределения, а также критические значения, которые отсекают области (половины размера) на обоих концах выборочного распределения.
{{cite book}}: CS1 maint: другие ( ссылка )