Оценка максимального расстояния

Метод оценки параметров статистической модели

Метод максимального расстояния пытается найти функцию распределения, такую, что расстояния D _{( i )} будут приблизительно одинаковой длины. Это делается путем максимизации их геометрического среднего .

В статистике оценка максимального интервала ( MSE или MSP ) или оценка максимального произведения интервала (MPS) — это метод оценки параметров одномерной статистической модели . ^[1] Метод требует максимизации геометрического среднего интервалов в данных, которые представляют собой разности между значениями кумулятивной функции распределения в соседних точках данных.

Концепция, лежащая в основе метода, основана на интегральном преобразовании вероятности , в том смысле, что набор независимых случайных выборок, полученных из любой случайной величины, должен в среднем быть равномерно распределен относительно кумулятивной функции распределения случайной величины. Метод MPS выбирает значения параметров, которые делают наблюдаемые данные максимально однородными, в соответствии с определенной количественной мерой однородности.

Один из наиболее распространенных методов оценки параметров распределения по данным, метод максимального правдоподобия (ММП), может дать сбой в различных случаях, например, при использовании определенных смесей непрерывных распределений. ^[2] В этих случаях метод оценки максимального интервала может оказаться успешным.

Помимо использования в чистой математике и статистике, сообщалось о пробных применениях метода с использованием данных из таких областей, как гидрология , ^[3] эконометрика , ^[4] магнитно-резонансная томография , ^[5] и других. ^[6]

История и использование

Метод MSE был выведен независимо Расселом Ченгом и Ником Амином из Института науки и технологий Уэльского университета и Бо Раннеби из Шведского университета сельскохозяйственных наук . ^[2] Авторы объяснили, что из-за преобразования интеграла вероятности при истинном параметре «расстояние» между каждым наблюдением должно быть равномерно распределено. Это означало бы, что разница между значениями кумулятивной функции распределения при последовательных наблюдениях должна быть одинаковой. Это тот случай, который максимизирует геометрическое среднее таких расстояний, поэтому решение для параметров, которые максимизируют геометрическое среднее, достигнет «наилучшего» соответствия, как определено таким образом. Раннеби (1984) обосновал метод, продемонстрировав, что он является оценщиком расхождения Кульбака–Лейблера , похожим на оценку максимального правдоподобия , но с более надежными свойствами для некоторых классов задач.

Существуют определенные распределения, особенно с тремя или более параметрами, чьи вероятности могут стать бесконечными вдоль определенных путей в пространстве параметров . Использование максимального правдоподобия для оценки этих параметров часто дает сбой, когда один параметр стремится к определенному значению, которое делает вероятность бесконечной, делая другие параметры несогласованными. Однако метод максимальных интервалов, зависящий от разницы между точками на кумулятивной функции распределения, а не от отдельных точек правдоподобия, не имеет этой проблемы и вернет достоверные результаты по гораздо более широкому массиву распределений. ^[1]

Распределения, которые, как правило, имеют проблемы с правдоподобием, часто используются для моделирования физических явлений. Холл и др. (2004) стремятся проанализировать методы смягчения последствий наводнений, что требует точных моделей эффектов речных наводнений. Распределения, которые лучше моделируют эти эффекты, представляют собой трехпараметрические модели, которые страдают от проблемы бесконечного правдоподобия, описанной выше, что привело к исследованию Холлом процедуры максимального расстояния. Вонг и Ли (2006), сравнивая метод с максимальным правдоподобием, используют различные наборы данных, начиная от набора по самому старшему возрасту смерти в Швеции между 1905 и 1958 годами до набора, содержащего ежегодные максимальные скорости ветра.

Определение

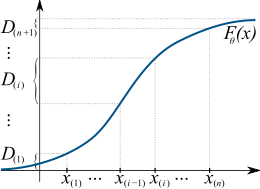
Дана случайная выборка iid { x ₁ , ..., x _n } размера n из одномерного распределения с непрерывной кумулятивной функцией распределения F ( x ; θ ₀ ), где θ ₀ ∈ Θ — неизвестный параметр, подлежащий оценке , пусть { x ₍₁₎ , ..., x _{( n )} } — соответствующая упорядоченная выборка, которая является результатом сортировки всех наблюдений от наименьшего к наибольшему. Для удобства также обозначим x ₍₀₎ = −∞ и x _{( n +1)} = +∞.

Определим интервалы как «пробелы» между значениями функции распределения в соседних упорядоченных точках: ^[7] $${\displaystyle D_{i}(\theta )=F(x_{(i)};\,\theta )-F(x_{(i-1)};\,\theta ),\quad i=1,\ldots ,n+1.}$$

Тогда максимальная оценка расстояния θ ₀ определяется как значение, которое максимизирует логарифм геометрического среднего расстояния между выборками: $${\displaystyle {\hat {\theta }}={\underset {\theta \in \Theta }{\operatorname {arg\,max} }}\;S_{n}(\theta ),\quad {\text{where }}\ S_{n}(\theta )=\ln \!\!{\sqrt[{n+1}]{D_{1}D_{2}\cdots D_{n+1}}}={\frac {1}{n+1}}\sum _{i=1}^{n+1}\ln {D_{i}}(\theta ).}$$

По неравенству средних арифметических и геометрических значений функция S _n ( θ ) ограничена сверху величиной −ln( n +1), и, таким образом, максимум должен существовать, по крайней мере, в смысле супремума .

Обратите внимание, что некоторые авторы определяют функцию S _n ( θ ) несколько иначе. В частности, Раннеби (1984) умножает каждый D _i на коэффициент ( n +1), тогда как Ченг и Стивенс (1989) опускают множитель 1 ⁄ n +1 перед суммой и добавляют знак «−», чтобы превратить максимизацию в минимизацию. Поскольку это константы относительно θ , модификации не изменяют местоположение максимума функции S _n .

Примеры

В этом разделе представлены два примера расчета оценки максимального расстояния.

Пример 1

Графики логарифмического значения λ для упрощенного примера при оценке как правдоподобия, так и расстояния. Значения, для которых и правдоподобие, и расстояние максимальны, оценки максимального правдоподобия и максимального расстояния, идентифицированы.

Предположим, что два значения x ₍₁₎ = 2, x ₍₂₎ = 4 были выбраны из экспоненциального распределения F ( x ; λ ) = 1 − e ^{− xλ} , x ≥ 0 с неизвестным параметром λ > 0. Чтобы построить MSE, мы должны сначала найти интервалы:

Процесс продолжается путем нахождения λ , которое максимизирует геометрическое среднее столбца «разность». Используя соглашение, которое игнорирует взятие корня ( n +1), это превращается в максимизацию следующего произведения: (1 − e ^{−2 λ} ) · (e ^{−2 λ} − e ^{−4 λ} ) · (e ^{−4 λ} ). Полагая μ = e ^{−2 λ} , задача становится нахождением максимума μ ⁵ −2 μ ⁴ + μ ³ . Дифференцируя, μ должно удовлетворять 5 μ ⁴ −8 μ ³ +3 μ ² = 0. Это уравнение имеет корни 0, 0,6 и 1. Поскольку μ на самом деле равно e ^{−2 λ} , оно должно быть больше нуля, но меньше единицы. Поэтому единственным приемлемым решением является , которое соответствует экспоненциальному распределению со средним значением 1 ⁄ λ ≈ 3,915. Для сравнения, оценка максимального правдоподобия λ является обратной величиной выборочного среднего значения, 3, поэтому λ _MLE = ⅓ ≈ 0,333. $${\displaystyle \mu =0.6\quad \Rightarrow \quad \lambda _{\text{MSE}}={\frac {\ln 0.6}{-2}}\approx 0.255,}$$

Пример 2

Предположим, что { x ₍₁₎ , ..., x _{( n )} } — упорядоченная выборка из равномерного распределения U ( a , b ) с неизвестными конечными точками a и b . Кумулятивная функция распределения равна F ( x ; a , b ) = ( x − a )/( b − a ), когда x ∈[ a , b ]. Поэтому индивидуальные интервалы задаются как $${\displaystyle D_{1}={\frac {x_{(1)}-a}{b-a}},\ \ D_{i}={\frac {x_{(i)}-x_{(i-1)}}{b-a}}\ {\text{for }}i=2,\ldots ,n,\ \ D_{n+1}={\frac {b-x_{(n)}}{b-a}}\ \ }$$

Вычислив геометрическое среднее и затем взяв логарифм, статистика S _n будет равна Здесь только три члена зависят от параметров a и b . Дифференцируя по этим параметрам и решая полученную линейную систему, максимальные оценки интервала будут $${\displaystyle S_{n}(a,b)={\tfrac {\ln(x_{(1)}-a)}{n+1}}+{\tfrac {\sum _{i=2}^{n}\ln(x_{(i)}-x_{(i-1)})}{n+1}}+{\tfrac {\ln(b-x_{(n)})}{n+1}}-\ln(b-a)}$$

${\displaystyle {\hat {a}}={\frac {nx_{(1)}-x_{(n)}}{n-1}},\ \ {\hat {b}}={\frac {nx_{(n)}-x_{(1)}}{n-1}}.}$

Известно, что они являются оценочными функциями с равномерно минимальной дисперсией и несмещенными функциями (UMVU) для непрерывного равномерного распределения. ^[1] Для сравнения, оценки максимального правдоподобия для этой задачи являются смещенными и имеют более высокую среднеквадратичную ошибку . ${\displaystyle \scriptstyle {\hat {a}}=x_{(1)}}$ ${\displaystyle \scriptstyle {\hat {b}}=x_{(n)}}$

Характеристики

Последовательность и эффективность

График функции плотности «J-образной» формы и ее соответствующее распределение. Смещенный Вейбулл с параметром масштаба 15, параметром формы 0,5 и параметром местоположения 10. Плотность асимптотически стремится к бесконечности, когда x приближается к 10, что делает оценки других параметров несостоятельными. Обратите внимание, что на графике распределения нет точки перегиба .

Оценка максимального интервала является последовательной оценкой в ​​том смысле, что она сходится по вероятности к истинному значению параметра θ ₀ , когда размер выборки увеличивается до бесконечности. ^[2] Последовательность оценки максимального интервала сохраняется при гораздо более общих условиях, чем для оценок максимального правдоподобия . В частности, в случаях, когда базовое распределение имеет форму буквы J, максимальное правдоподобие не будет работать там, где MSE работает. ^[1] Примером плотности в форме буквы J является распределение Вейбулла , в частности смещенный Вейбулл , с параметром формы меньше 1. Плотность будет стремиться к бесконечности, когда x приближается к параметру местоположения, делая оценки других параметров несостоятельными.

Оценки максимального интервала также по крайней мере столь же асимптотически эффективны , как и оценки максимального правдоподобия, где последние существуют. Однако MSE могут существовать в случаях, когда MLE отсутствуют. ^[1]

Чувствительность

Оценки максимального интервала чувствительны к близко расположенным наблюдениям, и особенно к связям. ^[8] Учитывая, что мы получаем $${\displaystyle X_{i+k}=X_{i+k-1}=\cdots =X_{i},\,}$$ $${\displaystyle D_{i+k}(\theta )=D_{i+k-1}(\theta )=\cdots =D_{i+1}(\theta )=0.\,}$$

Когда связи обусловлены множественными наблюдениями, повторяющиеся интервалы (те, которые в противном случае были бы равны нулю) следует заменить соответствующей вероятностью. ^[1] То есть следует заменить на , поскольку . ${\displaystyle f_{i}(\theta )}$ ${\displaystyle D_{i}(\theta )}$ $${\displaystyle \lim _{x_{i}\to x_{i-1}}{\frac {\int _{x_{i-1}}^{x_{i}}f(t;\theta )\,dt}{x_{i}-x_{i-1}}}=f(x_{i-1},\theta )=f(x_{i},\theta ),}$$ ${\displaystyle x_{i}=x_{i-1}}$

Когда связи возникают из-за ошибки округления, Ченг и Стивенс (1989) предлагают другой метод устранения эффектов. ^{[примечание 1]} При наличии r связанных наблюдений от x _i до x _{i + r −1} пусть δ представляет ошибку округления . Все истинные значения должны тогда попадать в диапазон . Соответствующие точки распределения теперь должны попадать между и . Ченг и Стивенс предлагают предположить, что округленные значения равномерно распределены в этом интервале, определяя ${\displaystyle x\pm \delta }$ ${\displaystyle y_{L}=F(x-\delta ,{\hat {\theta }})}$ ${\displaystyle y_{U}=F(x+\delta ,{\hat {\theta }})}$ $${\displaystyle D_{j}={\frac {y_{U}-y_{L}}{r-1}}\quad (j=i+1,\ldots ,i+r-1).}$$

Метод MSE также чувствителен к вторичной кластеризации. ^[8] Одним из примеров этого явления является ситуация, когда набор наблюдений считается полученным из одного нормального распределения , но на самом деле он получен из смеси нормалей с разными средними. Вторым примером является ситуация, когда данные считаются полученными из экспоненциального распределения , но на самом деле они получены из гамма-распределения . В последнем случае в нижнем хвосте могут встречаться меньшие интервалы. Высокое значение M ( θ ) будет указывать на этот эффект вторичной кластеризации и предполагать необходимость более внимательного изучения данных. ^[8]

тест Морана

Статистика S _n ( θ ) также является формой статистики Морана или Морана-Дарлинга, M ( θ ), которая может использоваться для проверки согласия . ^{[примечание 2]} Было показано, что статистика, если ее определить как , является асимптотически нормальной , и что для малых выборок существует приближение хи-квадрат. ^[8] В случае, когда мы знаем истинный параметр , Ченг и Стивенс (1989) показывают, что статистика имеет нормальное распределение с , где γ — константа Эйлера–Маскерони, которая приблизительно равна 0,57722. ^{[примечание 3]} $${\displaystyle S_{n}(\theta )=M_{n}(\theta )=-\sum _{j=1}^{n+1}\ln {D_{j}(\theta )},}$$ ${\displaystyle \theta ^{0}}$ ${\displaystyle \scriptstyle M_{n}(\theta )}$ $${\displaystyle {\begin{aligned}\mu _{M}&\approx (n+1)(\ln(n+1)+\gamma )-{\frac {1}{2}}-{\frac {1}{12(n+1)}},\\\sigma _{M}^{2}&\approx (n+1)\left({\frac {\pi ^{2}}{6}}-1\right)-{\frac {1}{2}}-{\frac {1}{6(n+1)}},\end{aligned}}}$$

Распределение также может быть аппроксимировано с помощью , где , в котором и где следует распределение хи-квадрат со степенями свободы . Поэтому для проверки гипотезы о том, что случайная выборка значений происходит из распределения , можно рассчитать статистику . Затем следует отклонить со значимостью , если значение больше критического значения соответствующего распределения хи-квадрат. ^[8] ${\displaystyle A}$ $${\displaystyle A=C_{1}+C_{2}\chi _{n}^{2}\,}$$ $${\displaystyle {\begin{aligned}C_{1}&=\mu _{M}-{\sqrt {\frac {\sigma _{M}^{2}n}{2}}},\\C_{2}&={\sqrt {\frac {\sigma _{M}^{2}}{2n}}},\\\end{aligned}}}$$ ${\displaystyle \chi _{n}^{2}}$ ${\displaystyle n}$ ${\displaystyle H_{0}}$ ${\displaystyle n}$ ${\displaystyle F(x,\theta )}$ ${\displaystyle T(\theta )={\frac {M(\theta )-C_{1}}{C_{2}}}}$ ${\displaystyle H_{0}}$ ${\displaystyle \alpha }$

Где θ ₀ оценивается с помощью , Ченг и Стивенс (1989) показали, что имеет то же асимптотическое среднее и дисперсию, что и в известном случае. Однако тестовая статистика, которая будет использоваться, требует добавления члена коррекции смещения и равна: где — число параметров в оценке. ${\displaystyle {\hat {\theta }}}$ ${\displaystyle S_{n}({\hat {\theta }})=M_{n}({\hat {\theta }})}$ $${\displaystyle T({\hat {\theta }})={\frac {M({\hat {\theta }})+{\frac {k}{2}}-C_{1}}{C_{2}}},}$$ ${\displaystyle k}$

Обобщенный максимальный интервал

Альтернативные меры и интервалы

Раннеби и Экстрём (1997) обобщили метод MSE для аппроксимации других мер помимо меры Кульбака–Лейблера. Экстрём (1997) далее расширил метод для исследования свойств оценщиков, использующих интервалы более высокого порядка, где интервал m -го порядка будет определен как . ${\displaystyle F(X_{j+m})-F(X_{j})}$

Многомерные распределения

Ranneby & al. (2005) обсуждают расширенные методы максимального интервала для многомерного случая. Поскольку для нет естественного порядка , они обсуждают два альтернативных подхода: геометрический подход, основанный на ячейках Дирихле , и вероятностный подход, основанный на метрике «ближайшего соседнего шара». ${\displaystyle \mathbb {R} ^{k}(k>1)}$

Смотрите также

• Расхождение Кульбака–Лейблера
• Максимальная вероятность
• Распределение вероятностей

Примечания

1. В статье, по-видимому, есть несколько незначительных типографских ошибок. Например, в разделе 4.2 уравнение (4.1), округляющая замена для , не должно иметь логарифмического члена. В разделе 1 уравнение (1.2) определяется как само расстояние и является отрицательной суммой логарифмов . Если на этом этапе регистрируется, результат всегда ≤ 0, так как разность между двумя соседними точками на кумулятивном распределении всегда ≤ 1 и строго < 1, если только на концах нет только двух точек. Кроме того, в разделе 4.3 на странице 392 расчет показывает, что это дисперсия, которая имеет оценку MPS 6,87, а не стандартное отклонение . – Редактор ${\displaystyle D_{j}}$ ${\displaystyle D_{j}}$ ${\displaystyle M(\theta )}$ ${\displaystyle D_{j}}$ ${\displaystyle D_{j}}$ ${\displaystyle \textstyle {\tilde {\sigma ^{2}}}}$ ${\displaystyle \textstyle {\tilde {\sigma }}}$
2. В литературе родственные статистики называются статистиками Морана или Морана-Дарлинга. Например, Ченг и Стивенс (1989) анализируют форму, где определяется как указано выше. Вонг и Ли (2006) также используют ту же форму. Однако Бейрлант и др. (2001) используют форму с дополнительным фактором внутри логарифмированного суммирования. Дополнительные факторы будут иметь значение с точки зрения ожидаемого среднего значения и дисперсии статистики. Для согласованности в этой статье будет по-прежнему использоваться форма Ченга и Амина/Вонга и Ли. -- Редактор ${\displaystyle \scriptstyle M(\theta )=-\sum _{j=1}^{n+1}\log {D_{i}(\theta )}}$ ${\displaystyle \scriptstyle D_{i}(\theta )}$ ${\displaystyle \scriptstyle M_{n}=-\sum _{j=0}^{n}\ln {((n+1)(X_{n,i+1}-X_{n,i}))}}$ ${\displaystyle (n+1)}$
3. Вонг и Ли (2006) исключили из своего описания постоянную Эйлера–Маскерони . -- Редактор

Ссылки

Цитаты

1. Ченг и Амин (1983)
2. Раннеби (1984)
3. Холл и др. (2004)
4. Анатольев и Косенок (2004)
5. Печяк (2014)
6. Вонг и Ли (2006)
7. Пайк (1965)
8. Ченг и Стивенс (1989)

Цитируемые работы

• Анатольев, Станислав; Косенок, Григорий (2005). "Альтернатива максимальному правдоподобию на основе интервалов" (PDF) . Эконометрическая теория . 21 (2): 472–476. CiteSeerX  10.1.1.494.7340 . doi :10.1017/S0266466605050255. S2CID  123004317. Архивировано из оригинала (PDF) 2011-08-16 . Получено 2009-01-21 .
• Бейрлант, Дж.; Дудевич, Э.Дж.; Дьёрфи, Л.; ван дер Мейлен, Э.Ц. (1997). "Непараметрическая оценка энтропии: обзор" (PDF) . Международный журнал математических и статистических наук . 6 (1): 17–40. ISSN  1055-7490. Архивировано из оригинального (PDF) 5 мая 2005 г. . Получено 31 декабря 2008 г. . Примечание: ссылка на статью представляет собой обновленную версию 2001 года.
• Cheng, RCH; Amin, NAK (1983). «Оценка параметров в непрерывных одномерных распределениях со смещенным началом». Журнал Королевского статистического общества, серия B. 45 ( 3): 394–403. doi :10.1111/j.2517-6161.1983.tb01268.x. ISSN  0035-9246. JSTOR  2345411.
• Ченг, Р. К. Ч.; Стивенс, МА (1989). «Тест согласия с использованием статистики Морана с оцененными параметрами». Biometrika . 76 (2): 386–392. doi :10.1093/biomet/76.2.385.
• Ekström, Magnus (1997). "Обобщенные оценки максимального расстояния". Университет Умео, математический факультет . 6. ISSN  0345-3928. Архивировано из оригинала 14 февраля 2007 г. Получено 2008-12-30 .
• Холл, М. Дж.; ван ден Бугаард, Х. Ф. П.; Фернандо, Р. К.; Майнетт, А. Е. (2004). «Построение доверительных интервалов для частотного анализа с использованием методов повторной выборки». Гидрология и науки о системах Земли . 8 (2): 235–246. doi : 10.5194/hess-8-235-2004 . ISSN  1027-5606.
• Печяк, Томаш (2014). Оценка максимального шума интервала в фоновых данных МРТ с одной катушкой. Международная конференция IEEE по обработке изображений. Париж. С. 1743–1747. doi :10.1109/icip.2014.7025349.
• Пайк, Рональд (1965). «Расстояния». Журнал Королевского статистического общества, серия B. 27 ( 3): 395–449. doi :10.1111/j.2517-6161.1965.tb00602.x. ISSN  0035-9246. JSTOR  2345793.
• Раннеби, Бо (1984). «Метод максимального интервала. Метод оценки, связанный с методом максимального правдоподобия». Scandinavian Journal of Statistics . 11 (2): 93–112. ISSN  0303-6898. JSTOR  4615946.
• Раннеби , Бо; Экстрём, Магнус (1997). «Оценки максимального расстояния на основе различных метрик». Университет Умео, математический факультет . 5. ISSN  0345-3928. Архивировано из оригинала 14 февраля 2007 г. Получено 30 декабря 2008 г.
• Раннеби, Бо; Джаммаламадакаб, С. Рао; Тетеруковский, Алекс (2005). "Оценка максимального расстояния для многомерных наблюдений" (PDF) . Журнал статистического планирования и вывода . 129 (1–2): 427–446. doi :10.1016/j.jspi.2004.06.059 . Получено 31 декабря 2008 г. .
• Wong, TST; Li, WK (2006). "Заметка об оценке распределений экстремальных значений с использованием максимального произведения интервалов". Временные ряды и смежные темы: в память о Чинг-Зонг Вэе . Заметки к лекциям Института математической статистики – Серия монографий. Бичвуд, Огайо: Институт математической статистики. стр. 272–283. arXiv : math/0702830v1 . doi :10.1214/074921706000001102. ISBN 978-0-940600-68-3. S2CID  88516426.