

Круг широты или линия широты на Земле — это абстрактный небольшой круг с востока на запад , соединяющий все местоположения вокруг Земли (без учета высоты ) на заданной линии координат широты .
Круги широты часто называют параллелями , потому что они параллельны друг другу; то есть плоскости, содержащие любой из этих кругов, никогда не пересекаются друг с другом. Положение местоположения вдоль круга широты задается его долготой . Круги широты не похожи на круги долготы, которые все являются большими кругами с центром Земли посередине, поскольку круги широты становятся меньше по мере увеличения расстояния от экватора . Их длину можно вычислить с помощью общей функции синуса или косинуса . Например, 60-я параллель к северу или югу вдвое короче экватора (без учета небольшого сплющивания Земли на 0,335%), вытекая из . В проекции Меркатора или в проекции Галла-Петерса круг широты перпендикулярен всем меридианам . [1] На эллипсоиде или в сферической проекции все круги широты являются локсодромиями , за исключением экватора.
Широта окружности приблизительно равна углу между экватором и окружностью, с вершиной угла в центре Земли. Экватор находится на 0°, а Северный и Южный полюса находятся на 90° северной и 90° южной широты соответственно. Экватор является самой длинной окружностью широты и единственной окружностью широты, которая также является большим кругом. Таким образом, он перпендикулярен всем меридианам.
Между экватором и полюсами в каждом полушарии имеется 89 целых (целых градусов ) кругов широты , но их можно разделить на более точные измерения широты, и они часто представлены в виде десятичных градусов (например, 34,637° с.ш.) или с минутами и секундами (например, 22°14'26" ю.ш.).
На карте круги широты могут быть параллельными или нет, а их расстояние может варьироваться в зависимости от того, какая проекция используется для отображения поверхности Земли на плоскости. На равнопрямоугольной проекции с центром на экваторе круги широты горизонтальны, параллельны и равномерно распределены. На других цилиндрических и псевдоцилиндрических проекциях круги широты горизонтальны и параллельны, но могут быть распределены неравномерно, чтобы придать карте полезные характеристики. Например, на проекции Меркатора круги широты более широко расположены вблизи полюсов, чтобы сохранить локальные масштабы и формы, в то время как на проекции Галла-Петерса круги широты расположены более близко вблизи полюсов, чтобы сравнение площадей было точным. На большинстве нецилиндрических и непсевдоцилиндрических проекций круги широты не являются ни прямыми, ни параллельными.
Дуги кругов широты иногда используются в качестве границ между странами или регионами, где отсутствуют отличительные естественные границы (например, в пустынях), или когда искусственная граница проводится как «линия на карте», что было сделано в огромных масштабах во время Берлинской конференции 1884 года относительно огромных частей африканского континента. Североамериканские нации и государства также в основном были созданы прямыми линиями, которые часто являются частями кругов широты. Например, северная граница Колорадо проходит по 41° с.ш. , а южная граница — по 37° с.ш. Примерно половина длины границы между Соединенными Штатами и Канадой проходит по 49° с.ш.

Существует пять основных кругов широты, перечисленных ниже с севера на юг. Положение экватора фиксировано (90 градусов от оси вращения Земли), но широты других кругов зависят от наклона этой оси относительно плоскости земной орбиты, и поэтому не являются идеально фиксированными. Значения ниже приведены на 16 ноября 2024 года: [2]
Эти круги широты, за исключением экватора, обозначают границы между пятью основными географическими зонами .
Экватор — это окружность, которая равноудалена от Северного и Южного полюсов . Он делит Землю на Северное и Южное полушария . Из параллелей или кругов широты это самая длинная и единственная « большая окружность » (окружность на поверхности Земли с центром в центре Земли). Все остальные параллели меньше и центрированы только на земной оси.
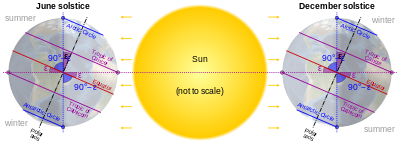
Полярный круг — самая южная широта в Северном полушарии, на которой Солнце может непрерывно находиться над или под горизонтом в течение 24 часов (в июньское и декабрьское солнцестояние соответственно). Аналогично, Южный полярный круг отмечает самую северную широту в Южном полушарии, на которой Солнце может непрерывно находиться над или под горизонтом в течение 24 часов (в декабрьское и июньское солнцестояние соответственно).
Широта полярных кругов равна 90° минус наклон земной оси .
Тропик Рака и тропик Козерога отмечают самую северную и самую южную широты, на которых Солнце можно увидеть прямо над головой во время июньского и декабрьского солнцестояния соответственно.
Широта тропических кругов равна наклону земной оси.
По определению, положения тропика Рака , тропика Козерога , полярного круга и южных полярных кругов зависят от наклона оси Земли относительно плоскости ее орбиты вокруг Солнца («наклон эклиптики»). Если бы Земля была «вертикальной» (ее ось была бы под прямым углом к плоскости орбиты), не было бы арктических, антарктических или тропических кругов: на полюсах Солнце всегда вращалось бы вдоль горизонта, а на экваторе Солнце всегда вставало бы точно на востоке, проходило бы прямо над головой и садилось точно на западе.
Положения тропического и полярного кругов не фиксированы, поскольку наклон оси меняется медленно – сложное движение, определяемое наложением множества различных циклов (некоторые из которых описаны ниже) с короткими и очень длинными периодами. В полдень 1 января 2000 года нашей эры среднее значение наклона составляло 23° 26′ 21.406″ (согласно теории P03 Международного астрономического союза 2006 года), соответствующее значение составляло 23° 26′ 10.633″ в полдень 1 января 2023 года нашей эры.
Основной долгосрочный цикл заставляет осевой наклон колебаться между примерно 22,1° и 24,5° с периодом 41 000 лет. В настоящее время среднее значение наклона уменьшается примерно на 0,468″ в год. В результате (приблизительно и в среднем) тропические круги дрейфуют к экватору (а полярные круги к полюсам) на 15 м в год, а площадь тропиков , определяемая астрономически, уменьшается на 1100 км 2 (420 кв. миль) в год. (Однако тропический пояс, определяемый на основе атмосферных условий, расширяется из-за глобального потепления . [3] )
Наклон земной оси имеет дополнительные краткосрочные изменения из-за нутации , из которых основной член с периодом 18,6 лет имеет амплитуду 9,2″ (что соответствует почти 300 м к северу и югу). [4] Существует много меньших членов, приводящих к различным суточным смещениям на несколько метров в любом направлении.
Наконец, ось вращения Земли не является строго фиксированной, а претерпевает небольшие колебания (порядка 15 м), называемые движением полюсов , которые оказывают небольшое влияние на тропики и полярные круги, а также на экватор.
Кратковременные колебания в течение нескольких дней не оказывают прямого влияния на положение крайних широт, на которых Солнце может оказаться прямо над головой, или на которых возможен 24-часовой день или ночь, за исключением случаев, когда они фактически происходят во время солнцестояний. Скорее, они вызывают теоретическое смещение параллелей, которое произошло бы, если бы заданный наклон оси сохранялся в течение всего года.
Эти круги широты могут быть определены на других планетах с наклонами осей относительно их орбитальных плоскостей. Такие объекты, как Плутон с углами наклона более 45 градусов, будут иметь тропические круги ближе к полюсам, а полярные круги ближе к экватору.
Ряд субнациональных и международных границ были предназначены для определения или аппроксимации параллелями. Параллели являются удобными границами в северном полушарии, поскольку астрономическую широту можно приблизительно измерить (с точностью до нескольких десятков метров), наведя на Полярную звезду .

Обычно круги широты определяются на нулевой высоте . Высота влияет на местоположение относительно плоскости, образованной кругом широты. Поскольку (в геодезической системе ) высота и глубина определяются нормалью к поверхности Земли, местоположения, имеющие одну и ту же широту, но разные высоты (т. е. лежащие вдоль этой нормали), больше не лежат в этой плоскости. Вместо этого все точки, имеющие одну и ту же широту, но разную высоту и долготу, занимают поверхность усеченного конуса, образованного вращением этой нормали вокруг оси вращения Земли.