Квантильно-параметризованное распределение

Квантильно -параметризованное распределение (КПР) — это распределение вероятностей, которое напрямую параметризуется данными. Они были созданы для удовлетворения потребности в простых в использовании непрерывных распределениях вероятностей, достаточно гибких для представления широкого спектра неопределенностей, таких как те, которые обычно встречаются в бизнесе, экономике, инженерии и науке. Поскольку КПР напрямую параметризуются данными, они имеют практическое преимущество, заключающееся в избежании промежуточного этапа оценки параметров — трудоемкого процесса, который обычно требует нелинейных итерационных методов для оценки параметров распределения вероятностей из данных. Некоторые КПР обладают практически неограниченной гибкостью формы и моментами замкнутой формы.

История

Разработка квантильно-параметризованных распределений была вдохновлена ​​практической потребностью в гибких непрерывных распределениях вероятностей, которые легко подгоняются под данные. Исторически семейства распределений Пирсона ^[1] и Джонсона ^{[2] [3]} использовались, когда требовалась гибкость формы. Это связано с тем, что оба семейства могут соответствовать первым четырем моментам (среднее, дисперсия, асимметрия и эксцесс) любого набора данных. Однако во многих случаях эти распределения либо трудно подгоняются под данные, либо недостаточно гибки, чтобы подгонять данные должным образом.

Например, бета-распределение — это гибкое распределение Пирсона, которое часто используется для моделирования процентов населения. Однако, если характеристики этого населения таковы, что желаемая кумулятивная функция распределения (CDF) должна проходить через определенные конкретные точки CDF, может не быть бета-распределения, которое удовлетворяло бы этой потребности. Поскольку бета-распределение имеет только два параметра формы, оно не может, в общем случае, соответствовать даже трем указанным точкам CDF. Более того, бета-параметры, которые наилучшим образом соответствуют таким данным, могут быть найдены только нелинейными итеративными методами.

Практики анализа решений , которым нужны распределения, легко параметризуемые тремя или более точками CDF (например, потому что такие точки были указаны в результате процесса выявления экспертов ), изначально изобрели для этой цели квантильно-параметризованные распределения. Килин и Поули (2011) ^[4] предоставили оригинальное определение. Впоследствии Килин (2016) ^[5] разработал металог-распределения , семейство квантильно-параметризованных распределений, которое имеет практически неограниченную гибкость формы, простые уравнения и моменты замкнутой формы.

Определение

Килин и Поули ^[4] определяют квантильно-параметризованное распределение как распределение, квантильная функция (обратная CDF) которого может быть записана в виде

${\displaystyle F^{-1}(y)=\left\{{\begin{array}{cl}L_{0}&{\text{for }}y=0\\\sum _{i=1}^{n}a_{i}g_{i}(y)&{\text{for }}0<y<1\\L_{1}&{\mbox{for }}y=1\end{array}}\right.}$

где

${\displaystyle {\begin{array}{rcl}L_{0}&=&\lim _{y\rightarrow 0^{+}}F^{-1}(y)\\L_{1}&=&\lim _{y\rightarrow 1^{-}}F^{-1}(y)\end{array}}}$

и функции являются непрерывно дифференцируемыми и линейно независимыми базисными функциями. Здесь, по сути, и являются нижней и верхней границами (если они существуют) случайной величины с функцией квантиля . Эти распределения называются квантильно-параметризованными, потому что для заданного набора пар квантилей , где , и набора базисных функций , коэффициенты могут быть определены путем решения набора линейных уравнений. ^[4] Если кто-то хочет использовать больше пар квантилей, чем базисных функций, то коэффициенты могут быть выбраны так, чтобы минимизировать сумму квадратов ошибок между указанными квантилями и . Килин и Поули ^[4] иллюстрируют эту концепцию для конкретного выбора базисных функций, который является обобщением функции квантиля нормального распределения , , для которого среднее значение и стандартное отклонение являются линейными функциями кумулятивной вероятности : ${\displaystyle g_{i}(y)}$ ${\displaystyle L_{0}}$ ${\displaystyle L_{1}}$ ${\displaystyle F^{-1}(y)}$ ${\displaystyle \{(x_{i},y_{i})\mid i=1,\ldots ,n\}}$ ${\displaystyle x_{i}=F^{-1}(y_{i})}$ ${\displaystyle n}$ ${\displaystyle g_{i}(y)}$ ${\displaystyle a_{i}}$ ${\displaystyle a_{i}}$ ${\displaystyle x_{i}}$ ${\displaystyle F^{-1}(y_{i})}$ ${\displaystyle x=\mu +\sigma \Phi ^{-1}(y)}$ ${\displaystyle \mu }$ ${\displaystyle \sigma }$ ${\displaystyle y}$

${\displaystyle \mu (y)=a_{1}+a_{4}y}$

${\displaystyle \sigma (y)=a_{2}+a_{3}y}$

Результатом является распределение с четырьмя параметрами, которое может быть точно подогнано к набору из четырех пар квантиль/вероятность или к любому количеству таких пар с помощью линейного метода наименьших квадратов . Килин и Поули ^[4] называют это простым Q-нормальным распределением. Некоторые перекошенные и симметричные простые Q-нормальные PDF показаны на рисунках ниже.

Симметричные простые Q-нормальные PDF-файлы

Перекошенные простые Q-нормальные PDF-файлы

Характеристики

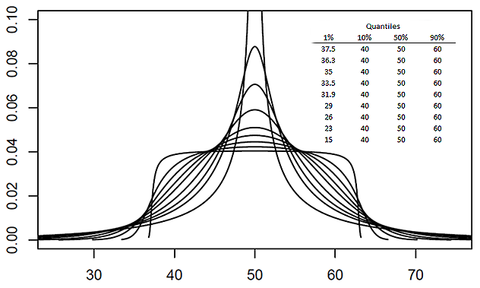
QPD, соответствующие определению Килина и Поули, обладают следующими свойствами.

Функция плотности вероятности

Дифференцирование по отношению к дает . Обратная величина этой величины, , является функцией плотности вероятности (PDF) ${\displaystyle x=F^{-1}(y)=\sum _{i=1}^{n}a_{i}g_{i}(y)}$ ${\displaystyle y}$ ${\displaystyle dx/dy}$ ${\displaystyle dy/dx}$

${\displaystyle f(y)=\left(\sum _{i=1}^{n}a_{i}{{dg_{i}(y)} \over {dy}}\right)^{-1}}$

где . Обратите внимание, что эта PDF выражена как функция кумулятивной вероятности, а не . Чтобы построить ее, как показано на рисунках, изменяйте параметрически. Постройте график на горизонтальной оси и на вертикальной оси. ${\displaystyle 0<y<1}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y\in (0,1)}$ ${\displaystyle x=F^{-1}(y)}$ ${\displaystyle f(y)}$

Осуществимость

Функция вида является допустимым распределением вероятностей тогда и только тогда, когда для всех . ^[4] Это подразумевает ограничение допустимости на набор коэффициентов : ${\displaystyle F^{-1}(y)}$ ${\displaystyle f(y)>0}$ ${\displaystyle y\in (0,1)}$ ${\displaystyle {\boldsymbol {a}}=(a_{1},\ldots ,a_{n})\in \mathbb {R} ^{n}}$

${\displaystyle \sum _{i=1}^{n}a_{i}{{dg_{i}(y)} \over {dy}}>0}$для всех ${\displaystyle y\in (0,1)}$

В практических приложениях осуществимость обычно следует проверять, а не предполагать.

Выпуклость

Набор допустимых коэффициентов QPD для всех является выпуклым . Поскольку выпуклая оптимизация требует выпуклых допустимых наборов, это свойство упрощает оптимизационные приложения, включающие QPD. ${\displaystyle S_{\boldsymbol {a}}=\{{\boldsymbol {a}}\in \mathbb {R} ^{n}\mid \sum _{i=1}^{n}a_{i}dg_{i}(y)/dy>0}$ ${\displaystyle y\in (0,1)\}}$

Соответствие данным

Коэффициенты могут быть определены из данных с помощью линейных наименьших квадратов . При наличии точек данных , которые предназначены для характеристики CDF QPD, и матрицы , элементы которой состоят из , тогда, при условии, что является обратимым, вектор-столбец коэффициентов может быть определен как , где и вектор-столбец . Если , это уравнение сводится к , где результирующая CDF проходит через все точки данных точно. Альтернативный метод, реализованный как линейная программа, определяет коэффициенты путем минимизации суммы абсолютных расстояний между CDF и данными, подлежащими ограничениям осуществимости. ^[6] ${\displaystyle {\boldsymbol {a}}}$ ${\displaystyle m}$ ${\displaystyle (x_{i},y_{i})}$ ${\displaystyle m\times n}$ ${\displaystyle {\boldsymbol {Y}}}$ ${\displaystyle g_{j}(y_{i})}$ ${\displaystyle {\boldsymbol {Y}}^{T}{\boldsymbol {Y}}}$ ${\displaystyle {\boldsymbol {a}}}$ ${\displaystyle {\boldsymbol {a}}=({\boldsymbol {Y}}^{T}{\boldsymbol {Y}})^{-1}{\boldsymbol {Y}}^{T}{\boldsymbol {x}}}$ ${\displaystyle m\geq n}$ ${\displaystyle {\boldsymbol {x}}=(x_{1},\ldots ,x_{m})}$ ${\displaystyle m=n}$ ${\displaystyle {\boldsymbol {a}}={\boldsymbol {Y}}^{-1}{\boldsymbol {x}}}$

Гибкость формы

QPD с членами, где , имеет параметры формы. Таким образом, QPD могут быть гораздо более гибкими, чем распределения Пирсона , которые имеют максимум два параметра формы. Например, было показано, что десятичленные металогарифмические распределения, параметризованные 105 точками CDF из 30 традиционных исходных распределений (включая нормальное, t-распределение Стьюдента, логнормальное, гамма, бета и экстремальное значение), приближают каждое такое исходное распределение в пределах расстояния K–S 0,001 или меньше. ^[7] ${\displaystyle n}$ ${\displaystyle n\geq 2}$ ${\displaystyle n-2}$

Трансформации

Преобразования QPD управляются общим свойством квантильных функций: для любой квантильной функции и возрастающая функция является квантильной функцией . ^[8] Например, квантильная функция нормального распределения , , является QPD по определению Килина и Поули. Натуральный логарифм , является возрастающей функцией, поэтому является квантильной функцией логнормального распределения с нижней границей . Важно отметить, что это преобразование преобразует неограниченную QPD в полуограниченную QPD. Аналогично, применение этого логарифмического преобразования к неограниченному распределению металога ^[9] дает полуограниченное (логарифмическое) распределение металога ; ^[10] аналогично, применение логит-преобразования , дает ограниченное (логарифмическое) распределение металога ^[10] с нижней и верхней границами и , соответственно. Более того, рассматривая распределенным , где есть любой QPD, который соответствует определению Килина и Поули, преобразованная переменная сохраняет вышеуказанные свойства осуществимости, выпуклости и соответствия данным. Такие преобразованные QPD имеют большую гибкость формы, чем базовый , который имеет параметры формы; логарифмическое преобразование имеет параметры формы, а логит-преобразование имеет параметры формы. Более того, такие преобразованные QPD имеют тот же набор допустимых коэффициентов, что и базовый непреобразованный QPD. ^[11] ${\displaystyle x=Q(y)}$ ${\displaystyle t(x),x=t^{-1}(Q(y))}$ ${\displaystyle x=\mu +\sigma \Phi ^{-1}(y)}$ ${\displaystyle t(x)=\ln(x-b_{l})}$ ${\displaystyle x=b_{l}+e^{\mu +\sigma \Phi ^{-1}(y)}}$ ${\displaystyle b_{l}}$ ${\displaystyle t(x)=\ln((x-b_{l})/(b_{u}-x))}$ ${\displaystyle b_{l}}$ ${\displaystyle b_{u}}$ ${\displaystyle t(x)}$ ${\displaystyle F^{-1}(y)}$ ${\displaystyle F^{-1}(y)}$ ${\displaystyle F^{-1}(y)}$ ${\displaystyle n-2}$ ${\displaystyle n-1}$ ${\displaystyle n}$

Моменты

Момент QPD равен: ^[4] ${\displaystyle k^{th}}$

${\displaystyle E[x^{k}]=\int _{0}^{1}\left(\sum _{i=1}^{n}a_{i}g_{i}(y)\right)^{k}dy}$

Существуют ли такие моменты в замкнутой форме, зависит от выбора базисных функций QPD . Неограниченное металог-распределение и полиномиальные QPD являются примерами QPD, для которых моменты существуют в замкнутой форме как функции коэффициентов . ${\displaystyle g_{i}(y)}$ ${\displaystyle a_{i}}$

Моделирование

Поскольку функция квантиля выражается в замкнутой форме, квантовые функции распределения Килина и Поули облегчают моделирование Монте-Карло . Подстановка в равномерно распределенные случайные выборки дает случайные выборки в замкнутой форме, тем самым устраняя необходимость инвертировать CDF, выраженную как . ${\displaystyle x=F^{-1}(y)}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y=F(x)}$

Связанные дистрибутивы

Следующие распределения вероятностей являются QPD согласно определению Килина и Поули:

• Квантильная функция нормального распределения , . ${\displaystyle x=\mu +\sigma \Phi ^{-1}(y)}$
• Квантильная функция распределения Гумбеля , . ${\displaystyle x=\mu -\beta \ln(-\ln(y))}$
• Квантильная функция распределения Коши , . ${\displaystyle x=x_{0}+\gamma \tan[\pi (y-0.5)]}$
• Квантильная функция логистического распределения , . ${\displaystyle x=\mu +s\ln(y/(1-y))}$
• Неограниченное распределение металогарифма , представляющее собой разложение в степенной ряд параметров и функции логистического квантиля. ${\displaystyle \mu }$ ${\displaystyle s}$
• Полуограниченные и ограниченные металогарифмические распределения , которые являются логарифмическим и логит-преобразованиями соответственно неограниченного металогарифмического распределения.
• Неограниченные, полуограниченные и ограниченные распределения металогов SPT (симметрично-процентильный триплет) , которые параметризуются тремя точками CDF и необязательными верхними и нижними границами.
• Простое Q-нормальное распределение ^[12]
• Метараспределения, включая метанормальное ^[13]
• Квантильные функции, выраженные в виде полиномиальных функций кумулятивной вероятности , включая полиномиальные функции Чебышева . ${\displaystyle y}$

Подобно металоговым распределениям SPT, квантильно-параметризованные распределения Джонсона ^{[14] [15]} (JQPD) параметризуются тремя квантилями. JQPD не соответствуют определению QPD Килина и Поули, а имеют свои собственные свойства. JQPD возможны для всех наборов параметров SPT, которые согласуются с правилами вероятности .

Приложения

Первоначально QPD применялись аналитиками решений, желающими удобно преобразовать оцененные экспертами квантили (например, 10-й, 50-й и 90-й квантили) в гладкие непрерывные распределения вероятностей. QPD также использовались для подгонки выходных данных из моделирования с целью представления этих выходных данных (как CDF, так и PDF) в виде непрерывных распределений в замкнутой форме. ^[16] При таком использовании они обычно более стабильны и гладкие, чем гистограммы. Аналогично, поскольку QPD могут накладывать меньше ограничений на форму, чем традиционные распределения, они использовались для подгонки широкого диапазона эмпирических данных с целью представления этих наборов данных в виде непрерывных распределений (например, отражая бимодальность, которая может существовать в данных, простым способом ^[17] ). Параметризация квантилей позволяет получить представление QPD в замкнутой форме известных распределений, чьи CDF в противном случае не имеют выражения в замкнутой форме. Килин и др. (2019) ^[18] применяют это к сумме независимых одинаково распределенных логнормальных распределений, где квантили суммы могут быть определены большим количеством симуляций. Девять таких квантилей используются для параметризации полуограниченного распределения металога, которое проходит через каждый из этих девяти квантилей точно. QPD также применялись для оценки рисков удара астероида, ^[19] кибербезопасности, ^{[6] [20]} смещений в прогнозах добычи нефти по сравнению с наблюдаемой добычей постфактум, ^[21] и будущих прогнозов населения Канады, основанных на объединении вероятностных взглядов нескольких экспертов. ^[22] См. распределения металога и Keelin (2016) ^[5] для дополнительных приложений распределения металога.

Внешние ссылки

• Дистрибуция Metalog, www.metalogs.org

Ссылки

1. Джонсон Н. Л., Коц С., Балакришнан Н. Непрерывные одномерные распределения, том 1, второе издание, John Wiley & Sons, Ltd, 1994, стр. 15–25.
2. Джонсон, Н. Л. (1949). «Системы частотных кривых, созданных методами трансляции». Biometrika . 36 (1/2): 149–176. doi :10.2307/2332539. JSTOR  2332539. PMID  18132090.
3. Тадикамалла, Панду Р.; Джонсон, Норман Л. (1982). «Системы частотных кривых, генерируемых преобразованиями логистических переменных». Biometrika . 69 (2): 461–465. doi :10.1093/biomet/69.2.461. JSTOR  2335422.
4. Килин, Томас В.; Паули, Брэдфорд В. (2011). «Квантильно-параметризованные распределения». Анализ решений . 8 (3): 206–219. дои : 10.1287/дека.1110.0213.
5. Keelin, Thomas W. (2016). «Распределения металогов». Анализ решений . 13 (4): 243–277. doi :10.1287/deca.2016.0338.
6. Faber, Isaac Justin; Paté-Cornell, M. Elisabeth; Lin, Herbert; Shachter, Ross D. (2019). Управление киберрисками: предупреждения об угрозах, генерируемые искусственным интеллектом (диссертация). Стэнфордский университет.
7. Килин, Томас В. (2016). «Распределения металогов». Анализ решений . 13 (4). Таблица 8. doi :10.1287/deca.2016.0338.
8. Гилкрист, В., 2000. Статистическое моделирование с квантильными функциями. CRC Press.
9. Килин, Томас В. (2016). «Распределения металогов». Анализ решений . 13 (4). Раздел 3, стр. 249–257. doi :10.1287/deca.2016.0338.
10. Keelin, Thomas W. (2016). "Распределения металогов". Анализ решений . 13 (4). Раздел 4. doi :10.1287/deca.2016.0338.
11. Powley, BW (2013). «Методы квантильных функций для анализа решений». Следствие 12, стр. 30. Докторская диссертация, Стэнфордский университет
12. Килин, Томас В.; Поули, Брэдфорд В. (2011). «Квантильно-параметризованные распределения». Анализ решений . 8 (3). стр. 208–210. doi :10.1287/deca.1110.0213.
13. Килин, Томас В. (2016). «Распределения металогов». Анализ решений . 13 (4): 253. doi :10.1287/deca.2016.0338.
14. Хэдлок, Кристофер С.; Бикель, Дж. Эрик (2017). «Параметризованные квантильными распределениями Джонсона». Анализ решений . 14 : 35–64. doi :10.1287/deca.2016.0343.
15. Хэдлок, Кристофер С.; Бикель, Дж. Эрик (2019). «Обобщенная система распределения Джонсона с квантильными параметрами». Анализ решений . 16 : 67–85. doi : 10.1287/deca.2018.0376. S2CID  159339224.
16. Килин, TW (2016), Раздел 6.2.2, стр. 271–274.
17. Килин, TW (2016), Раздел 6.1.1, Рисунок 10, стр. 266–267.
18. Mustafee, N. (18 мая 2020 г.). Распределения металогарифмов и чрезвычайно точные суммы логнормальных распределений в замкнутой форме. Институт инженеров по электротехнике и электронике (IEEE). стр. 3074–3085. ISBN 9781728132839.
19. Рейнхардт, Джейсон С.; Чэнь, Си; Лю, Вэньхао; Манчев, Петар; Пате-Корнелл, М. Элизабет (2016). «Оценка риска астероидов: вероятностный подход». Анализ риска . 36 (2): 244–261. Bibcode : 2016RiskA..36..244R. doi : 10.1111/risa.12453. PMID  26215051. S2CID  23308354.
20. Ван, Джиали; Нил, Мартин; Фентон, Норман (2020). «Байесовский сетевой подход к оценке рисков кибербезопасности, реализующий и расширяющий модель FAIR». Компьютеры и безопасность . 89 : 101659. doi : 10.1016/j.cose.2019.101659. S2CID  209099797.
21. Братволд, Рейдар Б.; Мохус, Эрленд; Петушниг, Дэвид; Бикель, Эрик (2020). «Прогнозирование добычи: оптимистично и самоуверенно — снова и снова». Spe Reservoir Evaluation & Engineering . 23 (3): 0799–0810. doi :10.2118/195914-PA. S2CID  219661316.
22. Развитие демографического прогнозирования (PDF) . Серия Springer по демографическим методам и анализу населения. Том 49. 2020. С. 43–62. doi : 10.1007/978-3-030-42472-5. hdl : 20.500.12657/42565. ISBN 978-3-030-42471-8. S2CID  226615299.