В математике точка Мисюревича — это значение параметра в множестве Мандельброта ( пространство параметров комплексных квадратичных отображений ), а также в действительных квадратичных отображениях интервала [1], для которых критическая точка строго предпериодична (т. е. становится периодической после конечного числа итераций, но сама по себе не является периодической). По аналогии, термин точка Мисюревича также используется для параметров в множестве мультиброта , где единственная критическая точка строго предпериодична. Этот термин имеет меньше смысла для отображений в большей общности, которые имеют более одной свободной критической точки, поскольку некоторые критические точки могут быть периодическими, а другие — нет. Эти точки названы в честь польско-американского математика Михала Мисюревича , который был первым, кто их изучал. [2]

Параметр является точкой Мисюревича, если он удовлетворяет уравнениям:
и:
так:
где:
Термин «точка Мисюревича» используется неоднозначно: Мисюревич первоначально исследовал отображения, в которых все критические точки были нерекуррентными; то есть, в которых существует окрестность для каждой критической точки, которую не посещает орбита этой критической точки. Это значение прочно установлено в контексте динамики итерированных интервальных отображений. [3] Только в очень особых случаях квадратичный многочлен имеет строго периодическую и единственную критическую точку. В этом ограниченном смысле этот термин используется в сложной динамике; более подходящим было бы название точки Мисюревича–Тёрстона (в честь Уильяма Терстона , который исследовал посткритически конечные рациональные отображения).
Комплексный квадратичный многочлен имеет только одну критическую точку. С помощью подходящего сопряжения любой квадратичный многочлен можно преобразовать в отображение вида , которое имеет единственную критическую точку в . Точки Мисюревича этого семейства отображений являются корнями уравнений:
При условии, что критическая точка не является периодической, где:
Например, точки Мисюревича с k = 2 и n = 1, обозначаемые M 2,1 , являются корнями:
Корень c = 0 не является точкой Мисюревича, поскольку критическая точка является неподвижной точкой при c = 0, и поэтому является периодической, а не предпериодической. Это оставляет единственную точку Мисюревича M 2,1 при c = −2.
Точки Мисюревича принадлежат границе множества Мандельброта и плотны на ней . [4] [5]
Если — точка Мисюревича, то соответствующее заполненное множество Жюлиа равно множеству Жюлиа , и это означает, что заполненное множество Жюлиа не имеет внутренней части .
Если — точка Мисюревича, то в соответствующем множестве Жюлиа все периодические циклы являются отталкивающими (в частности, цикл, на который попадает критическая орбита).
Множество Мандельброта и множество Жюлиа локально асимптотически самоподобны вокруг точек Мисюревича. [6]
Точки Мисюревича в контексте множества Мандельброта можно классифицировать на основе нескольких критериев. Одним из таких критериев является количество внешних лучей, которые сходятся в такой точке. [4] Точки ветвления, которые могут разделить множество Мандельброта на две или более подобластей, имеют три или более внешних аргумента (или углов) . Точки без ветвления имеют ровно два внешних луча (они соответствуют точкам, лежащим на дугах внутри множества Мандельброта). Эти точки без ветвления, как правило, более тонкие и сложные для идентификации в визуальных представлениях. Конечные точки, или кончики ветвления, имеют только один внешний луч, сходящийся в них. Другим критерием классификации точек Мисюревича является их появление на графике подмножества множества Мандельброта. Точки Мисюревича можно найти в центрах спиралей, а также в точках, где встречаются две или более ветвей. [7] Согласно теореме о ветвлении множества Мандельброта, [5] все точки ветвления множества Мандельброта являются точками Мисюревича. [4] [5]
Большинство параметров Мисюревича в множестве Мандельброта демонстрируют «центр спирали». [8] Это происходит из-за поведения при параметре Мисюревича, где критическое значение переходит на отталкивающий периодический цикл после конечного числа итераций. В каждой точке цикла множество Жюлиа демонстрирует асимптотическую самоподобность посредством комплексного умножения на производную этого цикла. Если производная недействительна, это означает, что множество Жюлиа вблизи периодического цикла имеет спиральную структуру. Следовательно, подобная спиральная структура возникает в множестве Жюлиа вблизи критического значения, и по теореме Тан Лея также в множестве Мандельброта вблизи любого параметра Мисюревича, для которого отталкивающая орбита имеет недействительный множитель. Видимость спиральной формы зависит от значения этого множителя. Количество ветвей в спирали соответствует количеству ветвей при параметре Мисюревича, которое, в свою очередь, равно количеству ветвей при критическом значении в множестве Жюлиа. Даже главная точка Мисюревича в 1/3-лимбе, расположенная в конце лучей параметров под углами 9/56, 11/56 и 15/56, асимптотически представляет собой спираль с бесконечным числом витков, хотя это трудно различить без увеличения. [ необходима цитата ]
Внешние аргументы точек Мисюревича, измеренные по ходам, следующие:
где: a и b — положительные целые числа, причем b — нечетное число, нижний индекс показывает основание системы счисления .
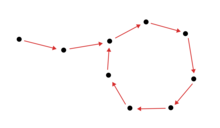
,.jpg/440px-Orbit_of_critical_point_z=0,_under_f(-2),.jpg)

Точка считается конечной точкой, поскольку она является кончиком нити, [10] и точкой приземления внешнего луча для угла 1/6. Ее критическая орбита . [11]
Точка считается конечной точкой, поскольку она является конечной точкой главной антенны множества Мандельброта. [12] и точкой приземления только одного внешнего луча (параметрического луча) угла 1/2. Она также считается конечной точкой, поскольку ее критическая орбита , [11] следуя символической последовательности = CLRRR ... с предварительным периодом 2 и периодом 1.
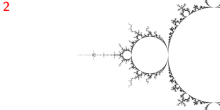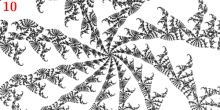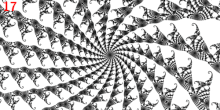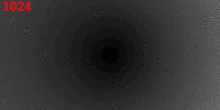

Точка считается точкой ветвления, поскольку она является главной точкой Мисюревича 1/3 колена и имеет 3 внешних луча: 9/56, 11/56 и 15/56.
Это точки, которые не являются ни ветвями, ни конечными точками.

Точка находится вблизи точки Мисюревича . Это видно, поскольку она является центром двухрукавной спирали, точкой приземления двух внешних лучей с углами: и где знаменатель равен , и имеет предпериодическую точку с предпериодом и периодом .
Точка находится вблизи точки Мисюревича , так как является точкой приземления для пары лучей: , и имеет предпериод и период .