Орбита перехода Хохмана

Маневр перехода между двумя орбитами

Орбита перехода Гомана, обозначенная 2, с орбиты (1) на более высокую орбиту (3)

Пример орбиты перехода Хохмана между Землей и Марсом, используемой зондом NASA InSight :
   Понимание  ·   Земля  ·   Марс

В космонавтике орбита перехода Хохмана ( / ˈ h oʊ m ə n / ) — орбитальный манёвр, используемый для перевода космического корабля между двумя орбитами разной высоты вокруг центрального тела. Например, перевод Хохмана может быть использован для перевода орбиты спутника с низкой околоземной орбиты на геостационарную орбиту . В идеализированном случае начальная и целевая орбиты являются круговыми и копланарными . Манёвр выполняется путём помещения корабля на эллиптическую переходную орбиту , которая является касательной как к начальной, так и к целевой орбитам. Манёвр использует два импульсных включения двигателя: первое устанавливает переходную орбиту, а второе корректирует орбиту для соответствия цели.

Маневр Хохмана часто использует наименьшее возможное количество импульса (которое потребляет пропорциональное количество delta-v , а значит и топлива ) для осуществления перехода, но требует относительно большего времени в пути, чем переходы с большим импульсом. В некоторых случаях, когда одна орбита намного больше другой, биэллиптический переход может использовать даже меньший импульс за счет еще большего времени в пути.

Манёвр был назван в честь Вальтера Хохмана , немецкого учёного, который опубликовал его описание в своей книге 1925 года « Достижимость небесных тел » ( Die Erreichbarkeit der Himmelskörper ). ^[1] Хохман находился под влиянием немецкого писателя-фантаста Курда Лассвица и его книги 1897 года «Две планеты» .

При использовании для путешествия между небесными телами орбита перехода Хохмана требует, чтобы начальная и конечная точки находились в определенных местах на их орбитах относительно друг друга. Космические миссии, использующие переход Хохмана, должны ждать, пока произойдет это требуемое выравнивание, что открывает окно запуска . Например, для миссии между Землей и Марсом эти окна запуска происходят каждые 26 месяцев. Орбита перехода Хохмана также определяет фиксированное время, необходимое для путешествия между начальной и конечной точками; для путешествия Земля-Марс это время путешествия составляет около 9 месяцев. Когда переход выполняется между орбитами, близкими к небесным телам со значительной гравитацией, обычно требуется гораздо меньше дельта-v , поскольку для сжигания может использоваться эффект Оберта .

Они также часто используются в таких ситуациях, но низкоэнергетические передачи , которые учитывают ограничения тяги реальных двигателей и используют преимущества гравитационных колодцев обеих планет, могут быть более экономичными. ^{[2] [3] [4]}

Пример

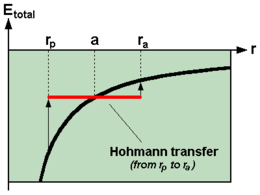
На схеме показана переходная орбита Хохмана для перевода космического корабля с нижней круговой орбиты на более высокую. Это эллиптическая орбита , которая касается как нижней круговой орбиты, которую должен покинуть космический корабль (голубой, обозначенный на схеме 1 ), так и более высокой круговой орбиты, которую он должен достичь (красный, обозначенный на схеме 3 ). Переходная орбита (желтый, обозначенный на схеме 2 ) инициируется включением двигателя космического корабля для добавления энергии и подъема апогея . Когда космический корабль достигает апогея, включается второй двигатель, добавляющий энергию для подъема перигея, переводя космический корабль на большую круговую орбиту.

Из-за обратимости орбит подобная переходная орбита Хохмана может быть использована для перевода космического корабля с более высокой орбиты на более низкую; в этом случае двигатель космического корабля запускается в направлении, противоположном его текущему пути, замедляя космический корабль и понижая его перигей до перигея эллиптической переходной орбиты. Затем двигатель снова запускается на более низком расстоянии, чтобы замедлить космический корабль до более низкой круговой орбиты. Переходная орбита Хохмана основана на двух мгновенных изменениях скорости . Дополнительное топливо требуется для компенсации того факта, что всплески занимают время; это минимизируется за счет использования двигателей с высокой тягой для минимизации продолжительности всплесков. Для переходов на околоземной орбите два включения называются включением перигея и включением апогея (или толчком апогея ^[5] ); в более общем смысле они называются включениями перицентра и апогея . В качестве альтернативы второе включение для придания орбите круговой формы может называться включением круговой формы .

Тип I и Тип II

Идеальная орбита перехода Хохмана перемещается между двумя круговыми орбитами в одной плоскости и проходит ровно 180° вокруг первичной. В реальном мире орбита назначения может быть не круговой и не копланарной с начальной орбитой. Реальные орбиты перехода могут проходить немного больше или немного меньше 180° вокруг первичной. Орбита, проходящая менее 180° вокруг первичной, называется переходом Хохмана «типа I», в то время как орбита, проходящая более 180°, называется переходом Хохмана «типа II». ^{[6] [7]}

Орбиты перехода могут проходить более чем на 360° вокруг первичной. Эти многооборотные переходы иногда называют типами III и IV, где тип III — это тип I плюс 360°, а тип IV — это тип II плюс 360°. ^[8]

Использует

Переходная орбита Хохмана может использоваться для переноса орбиты объекта к другому объекту, пока они находятся на одной орбите с более массивным телом. В контексте Земли и Солнечной системы это включает любой объект, который вращается вокруг Солнца . Примером того, где может использоваться переходная орбита Хохмана, является приведение астероида, вращающегося вокруг Солнца, в контакт с Землей. ^[9]

Расчет

Для малого тела, вращающегося вокруг другого гораздо большего тела, например, спутника, вращающегося вокруг Земли, полная энергия меньшего тела представляет собой сумму его кинетической энергии и потенциальной энергии , и эта полная энергия также равна половине потенциала на среднем расстоянии ( большая полуось ): ${\displaystyle a}$ $${\displaystyle E={\frac {mv^{2}}{2}}-{\frac {GMm}{r}}={\frac {-GMm}{2a}}.}$$

Решение этого уравнения относительно скорости приводит к уравнению vis-viva , где: $${\displaystyle v^{2}=\mu \left({\frac {2}{r}}-{\frac {1}{a}}\right),}$$

• ${\displaystyle v}$это скорость вращающегося тела,
• ${\displaystyle \mu =GM}$— стандартный гравитационный параметр первичного тела, предполагая, что он не намного больше (что составляет ), (для Земли это μ ~3,986E14 м ³ с ⁻² ) ${\displaystyle M+m}$ ${\displaystyle M}$ ${\displaystyle v_{M}\ll v}$
• ${\displaystyle r}$- расстояние орбитального тела от первичного фокуса,
• ${\displaystyle a}$большая полуось орбиты тела.

Следовательно, дельта- v (Δv), необходимая для перехода Хохмана, может быть вычислена следующим образом, в предположении мгновенных импульсов: для входа на эллиптическую орбиту в с круговой орбиты, где - афелий результирующей эллиптической орбиты, и для выхода с эллиптической орбиты в на круговую орбиту, где и - соответственно радиусы круговых орбит отправления и прибытия; меньшее (большее) из и соответствует расстоянию перицентра ( расстоянию апоцентра ) эллиптической переходной орбиты Хохмана. Обычно указывается в единицах м ³ /с ² , поэтому обязательно используйте метры, а не километры, для и . Тогда общая сумма будет равна: $${\displaystyle \Delta v_{1}={\sqrt {\frac {\mu }{r_{1}}}}\left({\sqrt {\frac {2r_{2}}{r_{1}+r_{2}}}}-1\right),}$$ ${\displaystyle r=r_{1}}$ ${\displaystyle r_{1}}$ ${\displaystyle r_{2}}$ $${\displaystyle \Delta v_{2}={\sqrt {\frac {\mu }{r_{2}}}}\left(1-{\sqrt {\frac {2r_{1}}{r_{1}+r_{2}}}}\right),}$$ ${\displaystyle r=r_{2}}$ ${\displaystyle r_{2}}$ ${\displaystyle r_{1}}$ ${\displaystyle r_{2}}$ ${\displaystyle r_{1}}$ ${\displaystyle r_{2}}$ ${\displaystyle \mu }$ ${\displaystyle r_{1}}$ ${\displaystyle r_{2}}$ ${\displaystyle \Delta v}$

$${\displaystyle \Delta v_{\text{total}}=\Delta v_{1}+\Delta v_{2}.}$$

Независимо от того, перемещаетесь ли вы на более высокую или более низкую орбиту, согласно третьему закону Кеплера ^{[ сломанный якорь ]} , время, необходимое для перехода между орбитами, равно

$${\displaystyle t_{\text{H}}={\frac {1}{2}}{\sqrt {\frac {4\pi ^{2}a_{\text{H}}^{3}}{\mu }}}=\pi {\sqrt {\frac {(r_{1}+r_{2})^{3}}{8\mu }}}}$$(половина орбитального периода для всего эллипса), где - длина большой полуоси переходной орбиты Гомана. ${\displaystyle a_{\text{H}}}$

Применительно к путешествию от одного небесного тела к другому важно начать маневр в момент, когда два тела будут правильно выровнены. Учитывая, что угловая скорость цели является угловым выравниванием α (в радианах ), в момент старта между исходным объектом и целевым объектом должно быть $${\displaystyle \omega _{2}={\sqrt {\frac {\mu }{r_{2}^{3}}}},}$$ $${\displaystyle \alpha =\pi -\omega _{2}t_{\text{H}}=\pi \left(1-{\frac {1}{2{\sqrt {2}}}}{\sqrt {\left({\frac {r_{1}}{r_{2}}}+1\right)^{3}}}\right).}$$

Пример

Полный энергетический баланс при гомановском переходе между двумя круговыми орбитами с первым радиусом и вторым радиусом ${\displaystyle r_{p}}$ ${\displaystyle r_{a}}$

Рассмотрим геостационарную переходную орбиту , начинающуюся с r ₁ = 6 678 км (высота 300 км) и заканчивающуюся на геостационарной орбите с r ₂ = 42 164 км (высота 35 786 км).

На меньшей круговой орбите скорость составляет 7,73 км/с; на большей — 3,07 км/с. На эллиптической орбите между ними скорость меняется от 10,15 км/с в перигее до 1,61 км/с в апогее.

Таким образом, Δv для первого импульса составляет 10,15 − 7,73 = 2,42 км/с, для второго импульса 3,07 − 1,61 = 1,46 км/с, а для обоих импульсов вместе 3,88 км/с.

Это больше , чем Δv, требуемое для орбиты спасения : 10,93 − 7,73 = 3,20 км/с. Применение Δv на низкой околоземной орбите (LEO) всего на 0,78 км/с больше (3,20−2,42) даст ракете скорость спасения , которая меньше Δv в 1,46 км/с, требуемой для закругления геосинхронной орбиты. Это иллюстрирует эффект Оберта , что на больших скоростях тот же Δv обеспечивает большую удельную орбитальную энергию , и увеличение энергии максимизируется, если тратить Δv как можно быстрее, а не тратить часть, замедляясь под действием гравитации, а затем тратить еще часть, чтобы преодолеть замедление (конечно, цель орбиты перехода Хохмана иная).

В худшем случае максимальная дельта-в

Как показывает пример выше, Δ v, требуемое для выполнения перехода Хохмана между двумя круговыми орбитами, не является наибольшим, когда радиус назначения бесконечен. (Скорость выхода составляет √ 2 от орбитальной скорости, поэтому Δ v, требуемое для выхода, составляет √ 2  − 1 (41,4%) от орбитальной скорости.) Требуемое Δ v является наибольшим (53,0% от меньшей орбитальной скорости), когда радиус большей орбиты составляет 15,5817... раз больше, чем радиус меньшей орбиты. ^[10] Это число является положительным корнем из x ³ − 15 x ² − 9 x − 1 = 0 , что равно . Для более высоких отношений орбит Δ v, требуемое для второго включения, уменьшается быстрее, чем увеличивается первое. ${\textstyle 5+4\,{\sqrt {7}}\cos \left({1 \over 3}\arctan {{\sqrt {3}} \over 37}\right)}$

Применение к межпланетным путешествиям

При использовании эффекта Оберта для перемещения космического корабля с орбиты одной планеты на орбиту другой он позволяет использовать дельта- v, меньшую , чем сумма дельта- v для отдельных маневров по уходу от первой планеты, с последующим переходом Хомана ко второй планете и последующим выходом на орбиту вокруг другой планеты.

Например, рассмотрим космический корабль, летящий с Земли на Марс . В начале своего путешествия космический корабль уже будет иметь определенную скорость и кинетическую энергию, связанную с его орбитой вокруг Земли. Во время работы ракетный двигатель применяет свою дельта- v , но кинетическая энергия увеличивается по квадратичному закону, пока ее не станет достаточно, чтобы вырваться из гравитационного потенциала планеты , а затем сжигает больше, чтобы получить достаточно энергии для выхода на переходную орбиту Хохмана (вокруг Солнца ). Поскольку ракетный двигатель способен использовать начальную кинетическую энергию топлива, требуется гораздо меньше дельта- v сверх того, что необходимо для достижения скорости убегания, и оптимальной ситуацией является ситуация, когда переходное включение производится на минимальной высоте (низкий перицентр ) над планетой. Требуемая дельта- v составляет всего 3,6 км/с, всего на 0,4 км/с больше, чем необходимо для выхода с Земли, хотя это приводит к тому, что космический корабль движется на 2,9 км/с быстрее Земли, направляясь к Марсу (см. таблицу ниже).

На другом конце космический корабль должен замедлиться, чтобы гравитация Марса захватила его. Этот захватный импульс должен оптимально выполняться на низкой высоте, чтобы также наилучшим образом использовать эффект Оберта. Поэтому для организации перехода необходимы относительно небольшие количества тяги на обоих концах пути по сравнению с ситуацией в свободном пространстве.

Однако при любом хохмановском переходе решающее значение имеет выравнивание двух планет на их орбитах — планета назначения и космический корабль должны прибыть в одну и ту же точку на своих соответствующих орбитах вокруг Солнца в одно и то же время. Это требование выравнивания порождает концепцию стартовых окон .

Термин «лунная переходная орбита» (ЛПО) используется для обозначения Луны .

Можно применить приведенную выше формулу для расчета Δv в км/с, необходимой для выхода на орбиту перехода Хохмана для прибытия в различные пункты назначения с Земли (предполагая, что планета имеет круговую орбиту). В этой таблице столбец с надписью «Δv для выхода на орбиту Хохмана с орбиты Земли» дает изменение от скорости Земли до скорости, необходимой для попадания на эллипс Хохмана, другой конец которого будет находиться на желаемом расстоянии от Солнца. Столбец с надписью «Высота НОО» дает необходимую скорость (в невращающейся системе отсчета с центром на Земле) на высоте 300 км над поверхностью Земли. Это получается путем прибавления к удельной кинетической энергии квадрата скорости убегания (10,9 км/с) с этой высоты. Столбец «НОО» — это просто предыдущая скорость за вычетом орбитальной скорости НОО 7,73 км/с.

Обратите внимание, что в большинстве случаев Δ v с низкой околоземной орбиты меньше Δ v для выхода на орбиту Хомана с орбиты Земли.

Чтобы добраться до Солнца, на самом деле не обязательно использовать Δ v в 24 км/с. Можно использовать 8,8 км/с, чтобы улететь очень далеко от Солнца, затем использовать пренебрежимо малую Δ v, чтобы свести угловой момент к нулю, а затем упасть на Солнце. Это можно считать последовательностью двух хомановских переходов, одного вверх и одного вниз. Кроме того, в таблице не указаны значения, которые будут применяться при использовании Луны для гравитационного маневра . Также есть возможности использовать одну планету, например Венеру, до которой легче всего добраться, чтобы помочь добраться до других планет или Солнца.

Сравнение с другими трансферами

Биэллиптический перенос

Биэллиптический переход состоит из двух полуэллиптических орбит . С начальной орбиты первый импульс расходует дельта-v для перевода космического корабля на первую переходную орбиту с апоцентром в некоторой точке вдали от центрального тела . В этой точке второй импульс отправляет космический корабль на вторую эллиптическую орбиту с перицентром в радиусе конечной желаемой орбиты, где выполняется третий импульс, выводящий космический корабль на желаемую орбиту. ^[11] ${\displaystyle r_{b}}$

Хотя для них требуется на одно включение двигателя больше, чем для перехода Хохмана, и, как правило, требуется больше времени на поездку, некоторые биэллиптические переходы требуют меньшего количества общей дельта-v, чем для перехода Хохмана, когда отношение конечной к начальной большой полуоси составляет 11,94 или больше, в зависимости от выбранной промежуточной большой полуоси. ^[12]

Идея биэллиптической траектории перехода была впервые ^{[ требуется ссылка ]} опубликована Ари Штернфельдом в 1934 году. ^[13]

Передача малой тяги

Двигатели малой тяги могут выполнять приближение к орбите перехода Хохмана, создавая постепенное расширение начальной круговой орбиты посредством тщательно рассчитанных по времени включений двигателя. Это требует изменения скорости (delta- v ) , которое больше, чем двухимпульсная орбита перехода ^[14] , и занимает больше времени для завершения.

Такие двигатели, как ионные двигатели, сложнее анализировать с помощью модели delta- v . Эти двигатели предлагают очень низкую тягу и в то же время гораздо более высокий бюджет delta- v , гораздо более высокий удельный импульс , меньшую массу топлива и двигателя. Маневр перехода Хохмана с двумя сгораниями был бы непрактичным при такой низкой тяге; маневр в основном оптимизирует использование топлива, но в этой ситуации его относительно много.

Если в ходе миссии планируются только маневры с малой тягой, то непрерывная работа двигателя с малой тягой, но очень высокой эффективностью может обеспечить более высокую дельта- v и в то же время использовать меньше топлива, чем обычный химический ракетный двигатель.

Переход с одной круговой орбиты на другую путем постепенного изменения радиуса требует просто той же дельта- v, что и разница между двумя скоростями. ^[14] Такой маневр требует большей дельта- v, чем двухскоростной маневр перехода Хохмана, но он выполняется с постоянной низкой тягой, а не с кратковременными применениями высокой тяги.

Количество использованной массы топлива измеряет эффективность маневра плюс используемое для него оборудование. Общая используемая delta- v измеряет эффективность только маневра. Для электрических двигательных систем, которые, как правило, имеют низкую тягу, высокая эффективность двигательной системы обычно компенсирует более высокую delta-V по сравнению с более эффективным маневром Хохмана.

Переходные орбиты с использованием электротяги или двигателей малой тяги оптимизируют время перехода для достижения конечной орбиты, а не delta-v, как в переходной орбите Хохмана. Для геостационарной орбиты начальная орбита устанавливается как суперсинхронная, и путем непрерывного толчка в направлении скорости в апогее переходная орбита трансформируется в круговую геосинхронную. Однако этот метод занимает гораздо больше времени из-за малой тяги, вводимой на орбиту. ^[15]

Межпланетная транспортная сеть

В 1997 году был опубликован набор орбит, известных как Межпланетная транспортная сеть (ITN), обеспечивающих еще более низкие тяговые дельта- v (хотя гораздо более медленные и длинные) пути между различными орбитами, чем орбиты перехода Хохмана. ^[16] Межпланетная транспортная сеть отличается по своей природе от переходов Хохмана, поскольку переходы Хохмана предполагают только одно большое тело, тогда как Межпланетная транспортная сеть этого не делает. Межпланетная транспортная сеть способна достичь использования менее тяговых дельта- v, используя гравитационную помощь от планет. ^{[ необходима цитата ]}

Смотрите также

• Космический портал

• Биэллиптический перенос
• Бюджет Delta-v
• Геостационарная переходная орбита
• Гало-орбита
• Орбита Лиссажу
• Список орбит
• Орбитальная механика

Цитаты

1. Уолтер Хохманн, Достижимость небесных тел (Вашингтон: Технический перевод НАСА F-44, 1960) Интернет-архив.
2. Уильямс, Мэтт (2014-12-26). «Как сделать путешествие на Марс дешевле и проще: аргументы в пользу баллистического захвата». Universe Today . Получено 29 июля 2019 г.
3. Хадхази, Адам. «Новый способ безопасно, в любое время и по дешевке достичь Марса». Scientific American . Получено 29 июля 2019 г.
4. "Введение в Берешит и его траекторию на Луну". Gereshes . 2019-04-08 . Получено 2019-07-29 .
5. Джонатан Макдауэлл, «Kick In the Apogee: 40 лет применения твердотопливных ракетных двигателей в верхних ступенях, 1957-1997», 33-я конференция AIAA Joint Propulsion Conference, 4 июля 1997 г. Аннотация. Получено 18 июля 2017 г.
6. NASA, Основы космического полета , Раздел 1, Глава 4, «Траектории». Получено 26 июля 2017 г. Также доступно spaceodyssey.dmns.org Архивировано 28 июля 2017 г. на Wayback Machine .
7. Тайсон Спаркс, Траектории к Марсу. Архивировано 28 октября 2017 г. в Wayback Machine , Колорадский центр астродинамических исследований, 14 декабря 2012 г. Получено 25 июля 2017 г.
8. Ланжевен, И. (2005). «Проблемы проектирования космических научных миссий», Полезная нагрузка и определение миссии в космических науках , В. Мартинес Пиллет, А. Апарисио и Ф. Санчес, ред., Cambridge University Press, стр. 30. ISBN 052185802X , 9780521858021 
9. Калла, Пабло; Фрайс, Дэн; Уэлч, Крис (2018). «Добыча полезных ископаемых на астероидах с помощью малых космических аппаратов и ее экономическая целесообразность». arXiv : 1808.05099 [astro-ph.IM].
10. Валладо, Дэвид Энтони (2001). Основы астродинамики и их применение. Springer. стр. 317. ISBN 0-7923-6903-3.
11. Кертис, Ховард (2005). Орбитальная механика для студентов-инженеров. Elsevier . стр. 264. ISBN 0-7506-6169-0.
12. Валладо, Дэвид Энтони (2001). Основы астродинамики и ее применение. Springer. стр. 318. ISBN 0-7923-6903-3.
13. Штернфельд, Ари Дж. (1934-02-12), "Sur les trajectoires permettant d'approcher d'un Corps attractif Central à partir d'une Orbite keplérienne donnée" [О разрешенных траекториях приближения к центральному притягивающему телу из с учетом кеплеровской орбиты], Comptes rendus de l'Académie des Sciences (на французском языке), 198 (1), Париж: 711–713..
14. MIT, 16.522: Space Propulsion , сессия 6, «Аналитические аппроксимации для маневров с малой тягой», весна 2015 г. (получено 26 июля 2017 г.)
15. Спитцер, Арнон (1997). Оптимальная траектория переходной орбиты с использованием электродвижения. USPTO .
16. Ло, М. В .; Росс, С. Д. (1997). «Путешествия по Солнечной системе: инвариантные многообразия и динамика Солнечной системы». Технический отчет . IOM. JPL . стр. 2–4. 312/97.

Общие и цитируемые источники

• Бейт, Р. Р.; Мюллер, Д. Д.; Уайт, Дж. Э. (1971). Основы астродинамики . Нью-Йорк: Dover Publications. ISBN 978-0-486-60061-1.
• Баттин, Р. Х. (1999). Введение в математику и методы астродинамики . Вашингтон, округ Колумбия: Американский институт аэронавтики и аст. ISBN 978-1-56347-342-5.
• Хоманн, Вальтер (1925). Die Erreichbarkeit der Himmelskörper . Мюнхен: Р. Ольденбург Верлаг. ISBN 3-486-23106-5.
• Торнтон, Стивен Т.; Мэрион, Джерри Б. (2003). Классическая динамика частиц и систем (5-е изд.). Брукс Коул . ISBN 0-534-40896-6.
• Валладо, ДА (2001). Основы астродинамики и ее применения (2-е изд.). Springer. ISBN 978-0-7923-6903-5.

Дальнейшее чтение

• "Орбитальная механика". Ракетно-космическая техника . Роберт А. Браеуниг. Архивировано из оригинала 2012-02-04 . Получено 2005-08-17 .
• "4. Межпланетные траектории". Основы космических полетов . JPL: NASA .