В геометрии и в ее приложениях к рисованию перспектива — это формирование изображения на картинной плоскости сцены, рассматриваемой из фиксированной точки.
Наука графической перспективы использует перспективности для создания реалистичных изображений в правильных пропорциях. По словам Кирсти Андерсен , первым автором, описавшим перспективу, был Леон Альберти в своей работе De Pictura (1435). [1] На английском языке Брук Тейлор представил свою «Линейную перспективу» в 1715 году, где он объяснил: «Перспектива — это искусство рисовать на плоскости видимость любых фигур по правилам геометрии». [2] Во второй книге, «Новые принципы линейной перспективы» (1719), Тейлор написал
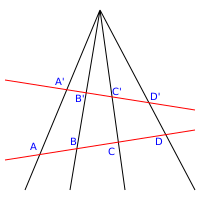
В проективной геометрии точки прямой называются проективным множеством , а множество прямых на плоскости относительно точки называется пучком .
Если заданы две прямые и в проективной плоскости и точка P этой плоскости ни на одной из прямых, то биективное отображение между точками области и областью , определяемой линиями пучка на P, называется перспективой (или, точнее, центральной перспективой с центром P ). [4] Специальный символ использовался для того, чтобы показать, что точки X и Y связаны перспективой; В этой нотации, чтобы показать, что центр перспективности — это P , запишите
Существование перспективности означает, что соответствующие точки находятся в перспективе . Двойственное понятие, осевая перспективность , представляет собой соответствие между линиями двух пучков, определяемое проективным диапазоном.
Композиция двух перспектив, в общем случае, не является перспективностью. Перспектива или композиция двух или более перспектив называется проективностью ( проективное преобразование , проективная коллинеация и гомография являются синонимами ).
Существует несколько результатов, касающихся проективностей и перспективностей, которые справедливы в любой папповской проективной плоскости: [5]
Теорема: Любая проективность между двумя различными проективными диапазонами может быть записана как композиция не более чем двух перспектив.
Теорема: Любая проективность из проективного ряда в себя может быть записана как композиция трех перспектив.
Теорема: Проективность между двумя различными проективными диапазонами, фиксирующая точку, является перспективностью.
Взаимооднозначное соответствие между точками на двух прямых в плоскости, определяемое точкой этой плоскости, не лежащей ни на одной из прямых, имеет многомерные аналоги, которые также будут называться перспективами.
Пусть S m и T m будут двумя различными m -мерными проективными пространствами, содержащимися в n -мерном проективном пространстве R n . Пусть P n − m −1 будет ( n − m − 1)-мерным подпространством R n , не имеющим общих точек ни с S m , ни с T m . Для каждой точки X из S m пространство L , натянутое на X и P n - m -1 , пересекает T m в точке Y = f P ( X ) . Это соответствие f P также называется перспективностью. [6] Центральная перспективность, описанная выше, имеет место при n = 2 и m = 1 .
Пусть S 2 и T 2 — две различные проективные плоскости в проективном 3-мерном пространстве R 3 . Поскольку O и O * не являются точками R 3 ни в одной из плоскостей, используйте конструкцию последнего раздела для проектирования S 2 на T 2 с помощью перспективности с центром O , за которой следует проекция T 2 обратно на S 2 с перспективностью с центром O *. Эта композиция является биективным отображением точек S 2 на себя, которое сохраняет коллинеарные точки и называется перспективной коллинеацией ( центральной коллинеацией в более современной терминологии). [7] Пусть φ — перспективная коллинеация S 2 . Каждая точка линии пересечения S 2 и T 2 будет зафиксирована φ, и эта линия называется осью φ . Пусть точка P будет пересечением линии OO * с плоскостью S 2 . P также зафиксирована φ, и каждая линия S 2 , которая проходит через P, стабилизируется φ (фиксированной, но не обязательно точечно фиксированной). P называется центром φ. Ограничение φ на любую прямую S2 , не проходящую через P, является центральной перспективой в S2 с центром P между этой прямой и прямой, которая является ее образом при φ.
