stringtranslate.com

Пирамида (геометрия)

В геометрии пирамида — это многогранник, образованный соединением многоугольного основания и точки, называемой вершиной . Каждое ребро основания и вершина образуют треугольник, называемый боковой гранью . Это коническое тело с многоугольным основанием. Многие типы пирамид можно найти, определив форму оснований или отрезав вершину. Его можно обобщить до более высокого измерения, известного как гиперпирамида . Все пирамиды самодвойственны .

Этимология

Слово «пирамида» происходит от древнегреческого термина «πυραμίς» (pyramis), который обозначал пирамидальную структуру и тип пшеничной лепешки. [1] [2] Термин происходит от греческих слов «πυρ» (pyr, «огонь») и «άμις» (amis, «сосуд»), что подчеркивает заостренный, похожий на пламя вид формы. [3]

В византийском греческом языке термин эволюционировал в «πυραμίδα» (pyramída), продолжая обозначать пирамидальные структуры. [4] Греческий термин «πυραμίς» был заимствован в латынь как «pyramis». Термин «πυραμίδα» повлиял на эволюцию слова в «pyramid» в английском и других языках. [5] [6]

Определение

Части пирамиды

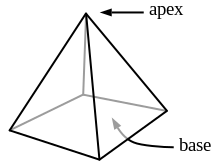
Пирамида — это многогранник, который может быть образован путем соединения многоугольного основания и точки, называемой вершиной . Каждое ребро основания и вершина образуют равнобедренный треугольник, называемый боковой гранью . [7] Ребра, соединенные от вершин многоугольного основания до вершины, называются боковыми ребрами . [8] Исторически определение пирамиды было описано многими математиками в древние времена. Евклид в своих «Началах» определил пирамиду как объемную фигуру, построенную из одной плоскости в одну точку. Контекст его определения был неясным, пока Герон Александрийский не определил ее как фигуру, соединив точку с многоугольным основанием. [9]

Призматоид определяется как многогранник, вершины которого лежат на двух параллельных плоскостях, а боковые грани — треугольники, трапеции и параллелограммы . [ 10] Пирамиды классифицируются как призматоиды. [11]

Классификация и типы

Семейство правильных многоугольных пирамид с основанием: тетраэдр, квадратная пирамида, пятиугольная пирамида и шестиугольная пирамида.

Правильная пирамида — это пирамида, основание которой описано около окружности, а высота пирамиды пересекается в центре окружности. [12] Эту пирамиду можно классифицировать на основе правильности ее оснований. Пирамида с правильным многоугольником в качестве основания называется правильной пирамидой . [13] Пирамида с n - сторонним правильным основанием имеет n + 1 вершину, n + 1 грань и 2 n ребер. [14] Такая пирамида имеет равнобедренные треугольники в качестве своих граней, с ее симметрией C n v , симметрией порядка 2 n : пирамиды симметричны, поскольку они вращаются вокруг своей оси симметрии (прямой, проходящей через вершину и центроид основания), и они зеркально симметричны относительно любой перпендикулярной плоскости, проходящей через биссектрису основания. [15] [16] Примерами являются квадратная пирамида и пятиугольная пирамида , пирамида с четырьмя и пятью треугольными гранями с квадратным и пятиугольным основанием соответственно; они классифицируются как первое и второе тело Джонсона, если их правильные грани и ребра равны по длине, а их симметрии равны C 4v порядка 8 и C 5v порядка 10 соответственно. [17] [18] Тетраэдр или треугольная пирамида — это пример, который имеет четыре равносторонних треугольника со всеми ребрами одинаковой длины, и одно из них считается основанием. Поскольку грани правильные , это пример Платонового тела и дельтаэдра , и он имеет тетраэдрическую симметрию . [19] [20] Пирамида с основанием в виде круга известна как конус . [21] Пирамиды обладают свойством самодвойственности , то есть их двойственные вершины совпадают с вершинами, соответствующими ребрам, и наоборот. [22] Их скелет может быть представлен в виде графа колеса . [23]

Пирамиды с прямоугольными и ромбическими основаниями

Правильная пирамида может также иметь основание в виде неправильного многоугольника. Примерами являются пирамиды с прямоугольником и ромбом в качестве оснований. Эти две пирамиды имеют симметрию C 2v порядка 4.

Тип пирамид может быть получен многими способами. Базовая регулярность основания пирамиды может быть классифицирована на основе типа многоугольника, и одним из примеров является пирамида с правильным звездчатым многоугольником в качестве ее основания, известная какЗвездная пирамида . [24] Пирамида, отсеченная плоскостью, называетсяусеченная пирамида ; если плоскость усечения параллельна основанию пирамиды, она называется усеченной .

Измерение

Площадь поверхности — это общая площадь граней каждого многогранника. В случае пирамиды площадь ее поверхности равна сумме площади треугольников и площади многоугольного основания.

Объем пирамиды равен одной трети произведения площади основания на высоту. Учитывая, что это площадь основания и это высота пирамиды. Математически объем пирамиды равен: [25] Объем пирамиды был записан еще в Древнем Египте, где они вычислили объем квадратного усеченного конуса , предполагая, что они знали объем квадратной пирамиды. [26] Формула объема для общей пирамиды была открыта индийским математиком Арьябхатой , где он процитировал в своей Арьябхатии , что объем пирамиды неправильно является половиной произведения площади основания на высоту. [27]

Обобщение

4-мерная гиперпирамида с кубом в основании

Гиперпирамида является обобщением пирамиды в n - мерном пространстве. В случае пирамиды соединяются все вершины основания, многоугольника на плоскости, с точкой вне плоскости, которая является вершиной . Высота пирамиды - это расстояние вершины от плоскости. Эта конструкция обобщается до n измерений. Основание становится ( n − 1) - многогранником в ( n − 1) - мерной гиперплоскости. Точка, называемая вершиной, находится вне гиперплоскости и соединяется со всеми вершинами многогранника, а расстояние вершины от гиперплоскости называется высотой. [28]

n - мерный объем n - мерной гиперпирамиды можно вычислить следующим образом: Здесь V n обозначает n - мерный объем гиперпирамиды. A обозначает ( n  − 1) - мерный объем основания, а h - высоту, то есть расстояние между вершиной и ( n  − 1) - мерной гиперплоскостью , содержащей основание A. [28 ]

Ссылки

  1. ^ "Генри Джордж Лидделл, Роберт Скотт, Греко-английский словарь, πυραμίς", www.perseus.tufts.edu.
  2. ^ Слово означало «вид пирога из жареных пшеничных зерен, консервированных в меду»; египетские пирамиды были названы в честь его формы. См. Beekes, Robert S. (2009), Etymological Dictionary of Greek , Brill, стр. 1261.
  3. ^ Лидделл, Генри Джордж; Скотт, Роберт (1940). Греко-английский лексикон . Clarendon Press.
  4. ^ "πυραμίδα" . Викисловарь . 12 июля 2022 г. Проверено 30 июня 2024 г.
  5. ^ Льюис, Чарльтон Т.; Шорт, Чарльз (1879). Латинский словарь . Clarendon Press.
  6. ^ Пек, Гарри Терстон (1898). Словарь классических древностей Харпера . Harper & Brothers.
  7. ^ Кромвель, Питер Р. (1997), Многогранники, Cambridge University Press, стр. 13.
  8. ^ Смит, Джеймс Т. (2000), Методы геометрии, John Wiley & Sons, стр. 98, ISBN 0-471-25183-6.
  9. ↑ Хит, Томас (1908), Евклид: Тринадцать книг «Начал», т. 3, Cambridge University Press, стр. 268.
  10. ^ Альсина, Клауди; Нельсен, Роджер Б. (2015), Математическая космическая одиссея: стереометрия в 21 веке, Математическая ассоциация Америки , стр. 85, ISBN 978-0-88385-358-0.
  11. ^ Грюнбаум, Бранко (1997), «Изогональные призматоиды», Дискретная и вычислительная геометрия , 18 : 13–52, doi :10.1007/PL00009307.
  12. ^ Полиа, Г. (1954), Математика и правдоподобное рассуждение: Индукция и аналогия в математике, Princeton University Press, стр. 138, ISBN 0-691-02509-6.
  13. ^ О'Лири, Майкл (2010), Революции геометрии, John Wiley & Sons, стр. 10, ISBN 978-0-470-59179-6.
  14. ^ Хамбл, Стив (2016), Экспериментатор от А до Я в математике: математические упражнения с компьютерной поддержкой, Тейлор и Фрэнсис, стр. 23, ISBN 978-1-134-13953-8.
  15. ^ Джонсон, Норман В. (2018), Геометрия и преобразования , Cambridge University Press, ISBN 978-1-107-10340-5. См. Главу 11: Конечные группы симметрии, 11.3 Пирамиды, призмы и антипризмы.
  16. ^ Александрофф, Пол (2012), Введение в теорию групп, Dover Publications, стр. 48, ISBN 978-0-486-48813-4.
  17. ^ Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Канадский журнал математики , 18 : 169–200, doi : 10.4153/cjm-1966-021-8 , MR  0185507, S2CID  122006114, Zbl  0132.14603. См. таблицу III, строка 1.
  18. ^ Уэхара, Рюхэй (2020), Введение в вычислительное оригами: мир новой вычислительной геометрии, Springer, стр. 62, doi :10.1007/978-981-15-4470-5, ISBN 978-981-15-4470-5.
  19. ^ Шавинина, Лариса В. (2013), Международный справочник Routledge по инновационному образованию, Routledge, стр. 333, ISBN 978-0-203-38714-6.
  20. ^ Канди, Х. Мартин (1952), «Дельтаэдры», The Mathematical Gazette , 36 (318): 263–266, doi : 10.2307/3608204, JSTOR  3608204, S2CID  250435684.
  21. ^ Келли, В. Майкл (2009), Огромная книга задач по геометрии, Penguin Group, стр. 455, ISBN 978-1-61564-698-2.
  22. ^ Wohlleben, Eva (2019), «Duality in Non-Polyhedral Bodies Part I: Polyliner», в Cocchiarella, Luigi (ред.), ICGG 2018 — Труды 18-й Международной конференции по геометрии и графике: 40-я годовщина — Милан, Италия, 3–7 августа 2018 г., Advances in Intelligent Systems and Computing, т. 809, Springer, стр. 485–486, doi : 10.1007/978-3-319-95588-9, ISBN 978-3-319-95588-9
  23. ^ Писански, Томаж; Серватиус, Бригитта (2013), Конфигурация с графической точки зрения, Springer, стр. 21, doi :10.1007/978-0-8176-8364-1, ISBN 978-0-8176-8363-4.
  24. ^ Веннингер, Магнус Дж. (1974), Модели многогранников, Cambridge University Press, стр. 50, ISBN 978-0-521-09859-5, архивировано из оригинала 2013-12-11
  25. ^ Александр, Дэниел С.; Кеберлин, Джерелин М. (2014), Элементарная геометрия для студентов колледжей (6-е изд.), Cengage Learning, стр. 403, ISBN 978-1-285-19569-8.
  26. ↑ Gillings, RJ (1964), «Объем усеченной пирамиды в древнеегипетских папирусах», The Mathematics Teacher , 57 (8): 552–555, doi :10.5951/MT.57.8.0552, JSTOR  27957144.
  27. ^ Каджори, Флориан (1991), История математики (5-е изд.), Американское математическое общество, стр. 87, ISBN 978-1-4704-7059-3.
  28. ^ ab Mathai, AM (1999), Введение в геометрическую вероятность: распределительные аспекты с приложениями, Taylor & Francis, стр. 42–43, ISBN 978-90-5699-681-9.

Смотрите также

Внешние ссылки

На Викискладе есть медиафайлы по теме Пирамиды (геометрия) .