Круговой турнир

Вид спортивного турнира

Пример кругового турнира с 10 участниками

Круговой турнир или турнир «все играют со всеми» — это формат соревнований, в котором каждый участник встречается с каждым другим участником, как правило, по очереди. ^{[1] [2]} Круговой турнир отличается от турнира на выбывание , в котором участники выбывают после определенного количества побед или поражений.

Терминология

Термин round-robin происходит от французского термина ruban ('лента'). Со временем термин стал идиомированным до robin . ^{[3] [4]}

В однокруговом расписании каждый участник играет с каждым другим участником один раз. Если каждый участник играет со всеми остальными дважды, это часто называется двойным круговым расписанием . Термин редко используется, когда все участники играют друг с другом более двух раз, ^[1] и никогда не используется, когда один участник играет с другими неравное количество раз, как это происходит почти во всех основных североамериканских профессиональных спортивных лигах.

В Соединенном Королевстве круговой турнир назывался американским турниром в таких видах спорта, как теннис или бильярд, которые обычно имеют турниры с выбыванием (или «нокаутом»), хотя сейчас это делается редко. ^{[5] [6] [7]}

Круговой турнир с четырьмя игроками иногда называют «квадом» или «четверкой». ^[8]

Приложения

В видах спорта с большим количеством соревновательных матчей за сезон распространены двухкруговые турниры. Большинство футбольных лиг в мире организованы по двухкруговой системе, в которой каждая команда играет со всеми остальными в своей лиге один раз дома и один раз на выезде. Эта система также используется в квалификации на крупные турниры, такие как чемпионат мира ФИФА и континентальные турниры (например, чемпионат Европы УЕФА , Золотой кубок КОНКАКАФ , Кубок Азии АФК , Кубок Америки КОНМЕБОЛ и Кубок Наций КАФ ). Существуют также круговые турниры по крикету , бриджу , шахматам , шашкам , го , хоккею с шайбой , керлингу и скрэбблу . Чемпионат мира по шахматам в 2005 и 2007 годах решил провести двухкруговой турнир из восьми игроков, где каждый игрок встречается с каждым другим игроком один раз как белый и один раз как черный. В этом формате проводилось несколько крупных международных турниров по крикету, включая мероприятия ICC , включая Кубок чемпионов ICC 2025 года . ^[9]

Более экстремальным примером может служить бейсбольная лига KBO , в которой используется 16-кратная круговая система, в которой каждая из 10 команд играет друг с другом 16 раз, что в общей сложности составляет 144 игры на команду.

LIDOM (Зимняя лига бейсбола в Доминиканской Республике) проводит 18-кратный круговой турнир в качестве полуфинального турнира между четырьмя классифицированными командами.

Рейтинги групповых турниров обычно составляются по количеству выигранных и сыгранных вничью матчей с использованием любого из множества дополнительных критериев.

Часто групповые этапы в рамках более широкого турнира проводятся по круговой системе. Примерами с расписанием с одним круговым механизмом являются чемпионат мира ФИФА , чемпионат Европы по футболу УЕФА и кубок УЕФА (2004–2009) в футболе, Супер регби ( регбийный союз ) в Южном полушарии во время его прошлых итераций как Супер 12 и Супер 14 (но не в его более поздних форматах с 15 и 18 командами), чемпионат мира по крикету вместе с Индийской премьер-лигой , крупный турнир по крикету Twenty-20 и многие конференции колледжей американского футбола , такие как Конференция США (которая в настоящее время насчитывает 9 членов). Групповые этапы клубных соревнований УЕФА и Кубок Либертадорес проводятся по двойной круговой системе, как и большинство баскетбольных лиг за пределами Соединенных Штатов, включая регулярный сезон Евролиги ( а также ее бывшую фазу Топ-16); Объединенная футбольная лига использовала двухкруговую систему в сезонах 2009 и 2010 годов .

Завершающие сезон теннисные турниры также используют круговой формат перед полуфиналами.

Оценка

Преимущества

Победителем кругового турнира становится участник, одержавший наибольшее количество побед, за исключением случаев, когда возможна ничья.

Теоретически круговой турнир — самый справедливый способ определить чемпиона из известного и фиксированного числа участников. Каждый участник, будь то игрок или команда, имеет равные шансы против всех остальных соперников, поскольку нет предварительного посева участников, который исключал бы матч между любой данной парой. Элемент удачи считается уменьшенным по сравнению с системой выбывания , поскольку одно или два плохих выступления не обязательно должны разрушить шансы участника на окончательную победу. Окончательные записи участников более точны в том смысле, что они представляют результаты за более длительный период против одного и того же соперника.

Система также лучше подходит для ранжирования всех участников, а не только для определения победителя. Это полезно для определения окончательного ранга всех участников, от сильнейшего к слабейшему, для целей квалификации на другой этап или соревнование, а также для получения призовых денег.

В командных видах спорта победители круговой системы высшей лиги обычно считаются «лучшей» командой в стране, а не обладатели кубка, турниры которых обычно проводятся по системе с выбыванием после одного поражения.

Более того, в таких турнирах, как чемпионаты мира FIFA или ICC, первый раунд, состоящий из ряда мини-раундов между группами из 4 команд, защищает от возможности того, что команда, проехавшая, возможно, тысячи миль, вылетит всего лишь после одного плохого выступления в системе прямого выбывания. Затем одна, две или иногда три лучшие команды в этих группах переходят в стадию прямого выбывания на оставшуюся часть турнира.

В круге смерти возможно, что в круговом турнире не будет чемпиона, даже если не будет ничьей, но в большинстве видов спорта существуют системы тай-брейка, которые решают эту проблему.

Недостатки

Круговые турниры могут страдать от того, что они слишком длинные по сравнению с другими типами турниров, а также от того, что более поздние запланированные игры потенциально не имеют существенного значения. Они также могут потребовать процедур разрешения конфликтов.

Турниры по швейцарской системе пытаются объединить элементы кругового формата и формата выбывания, чтобы выявить достойного чемпиона, используя меньше раундов, чем при круговой системе, допуская при этом ничьи и поражения.

Продолжительность турнира

Главным недостатком кругового турнира является время, необходимое для его завершения. В отличие от турнира на выбывание, где половина участников выбывает после каждого раунда, круговой турнир требует на один раунд меньше, чем количество участников. Например, турнир из 16 команд может быть завершен всего за 4 раунда (т. е. 15 матчей) в формате на выбывание; формат турнира с двойным выбыванием требует 30 (или 31) матчей, но круговой турнир потребует 15 раундов (т. е. 120 матчей), чтобы закончить, если каждый участник встретится друг с другом по одному разу.

Другие проблемы вытекают из разницы между теоретической справедливостью формата круговой системы и практикой в ​​реальном событии. Поскольку победитель постепенно определяется в ходе нескольких раундов игры, команды, которые выступают плохо и которые могли бы быстро выбыть из борьбы за титул, вынуждены играть свои оставшиеся игры. Таким образом, игры проводятся поздно в соревновании между участниками, у которых не остается никаких шансов на успех. Более того, в некоторых более поздних матчах один участник, у которого есть что-то, чтобы играть, будет с другим, у которого этого нет. Также может быть возможным, что участник будет играть с сильнейшими противниками в круговой системе в быстрой последовательности, в то время как другие будут играть с ними попеременно с более слабыми противниками. Эта асимметрия означает, что игра с теми же противниками не обязательно полностью справедлива.

Также не запланирован показательный финальный матч, если только (по совпадению) два участника не встретятся в последнем матче турнира, и результат этого матча определит чемпионство. Ярким примером такого события стал матч чемпионата мира по футболу FIFA 1950 между Уругваем и Бразилией .

Квалифицированные команды

Дополнительные проблемы возникают, когда круговая система используется в качестве отборочного тура в рамках более крупного турнира. Участник, уже прошедший квалификацию на следующий этап до своей последней игры, может либо не стараться изо всех сил (чтобы сохранить ресурсы для следующего этапа), либо даже намеренно проиграть (если запланированный соперник следующего этапа для квалификационного турнира с более низким местом воспринимается как более легкий, чем для турнира с более высоким местом).

Четыре пары в женском парном бадминтоне на Олимпийских играх 2012 года , прошедшие в следующий раунд, были исключены из соревнований за попытку проиграть на этапе круговой системы, чтобы избежать соотечественниц и соперников с более высоким рейтингом. ^[10] Этап круговой системы на Олимпийских играх был новым введением, и эти потенциальные проблемы были хорошо известны до турнира; изменения были внесены перед следующими Олимпийскими играми, чтобы предотвратить повторение этих событий.

Круг смерти

Другим недостатком, особенно в небольших круговых турнирах, является «круг смерти», когда команды не могут быть разделены по результатам личных встреч. В круговой системе из трех команд, где A побеждает B, B побеждает C, а C побеждает A, все три участника будут иметь результат в одну победу и одно поражение, и для разделения команд необходимо будет использовать тай-брейк. ^[11] Это известное событие произошло во время чемпионата мира по футболу FIFA 1994 года в группе E , где все четыре команды закончили с результатом в одну победу, одну ничью и одно поражение. Это явление аналогично парадоксу Кондорсе в теории голосования.

Алгоритм планирования

Если — число участников, то для чистого кругового турнира требуются игры. Если — четное, то в каждом раунде игры могут проводиться одновременно, при условии наличия достаточных ресурсов (например, кортов для теннисного турнира). Если — нечетное, то будут раунды, в каждом из которых будут игры, и один участник не будет играть в этом раунде. ${\displaystyle n}$ ${\displaystyle {\begin{matrix}{\frac {n}{2}}\end{matrix}}(n-1)}$ ${\displaystyle n}$ ${\displaystyle (n-1)}$ ${\displaystyle {\begin{matrix}{\frac {n}{2}}\end{matrix}}}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle {\begin{matrix}{\frac {n-1}{2}}\end{matrix}}}$

Метод круга

Круговой метод — это простой алгоритм для создания расписания для кругового турнира. Всем участникам присваиваются номера, а затем они разбиваются на пары в первом раунде:

Далее один из участников в первом или последнем столбце таблицы фиксируется (в данном примере это номер один), а остальные перемещаются по часовой стрелке на одну позицию:

Это повторяется до тех пор, пока следующая итерация не приведет к первоначальным парам:

При четном числе конкурентов этот алгоритм реализует все возможные их комбинации (что эквивалентно тому, что все реализованные пары попарно различны). ${\displaystyle n}$

Во-первых, алгоритм, очевидно, реализует каждую пару конкурентов, если один из них равен (неподвижный конкурент). ${\displaystyle 1}$

Далее, для пар неконкурентов пусть их расстояние будет равно количеству раз, которое необходимо выполнить вращение, чтобы один участник оказался на месте другого. ${\displaystyle 1}$ ${\displaystyle k<{\frac {n}{2}}}$

В приведенном примере ( ) имеет расстояние до и до , а также имеет расстояние до и до . ${\displaystyle n=14}$ ${\displaystyle 2}$ ${\displaystyle 1}$ ${\displaystyle 3}$ ${\displaystyle 14}$ ${\displaystyle 6}$ ${\displaystyle 8}$ ${\displaystyle 9}$

В раунде не крайнюю левую позицию (не включая ) могут занять только участники с фиксированной дистанцией. В раунде примера на второй позиции участник играет против , их дистанция составляет . В раунде эту позицию занимают участники и , также имеющие дистанцию ​​и т. д. Аналогично, следующую позицию ( против в раунде , против в раунде и т. д.) могут занимать только участники с дистанцией- . ${\displaystyle 1}$ ${\displaystyle 1}$ ${\displaystyle 2}$ ${\displaystyle 13}$ ${\displaystyle 2}$ ${\displaystyle 2}$ ${\displaystyle 14}$ ${\displaystyle 12}$ ${\displaystyle 2}$ ${\displaystyle 3}$ ${\displaystyle 12}$ ${\displaystyle 1}$ ${\displaystyle 2}$ ${\displaystyle 11}$ ${\displaystyle 2}$ ${\displaystyle 4}$

Для каждого существует ровно пар расстояний . Существуют раунды, и все они реализуют одну пару расстояний в одной и той же позиции. Очевидно, что эти пары попарно различны. Вывод заключается в том, что каждая пара расстояний реализуется. ${\displaystyle k<{\frac {n}{2}}}$ ${\displaystyle n-1}$ ${\displaystyle k}$ ${\displaystyle n-1}$ ${\displaystyle k}$ ${\displaystyle k}$

Это справедливо для каждого , следовательно, каждая пара реализуется. ${\displaystyle k}$

Если количество участников нечетное, можно добавить подставного участника, чей запланированный соперник в данном раунде не играет и имеет пропуск . Таким образом, расписание можно рассчитать так, как если бы подставной игрок был обычным игроком, либо постоянным, либо ротируемым.

Вместо ротации одной позиции, любое число, относительно простое к , сгенерирует полное расписание. Верхние и нижние ряды могут обозначать дома/в гостях в спорте, белые/черные в шахматах и ​​т. д.; для обеспечения справедливости это должно чередоваться между раундами, поскольку участник 1 всегда находится в первом ряду. Если, скажем, участники 3 и 8 не смогли выполнить свое задание в третьем раунде, его необходимо будет перенести за пределы других раундов, поскольку оба участника уже столкнутся с другими противниками в этих раундах. Более сложные ограничения расписания могут потребовать более сложных алгоритмов. ^[12] Это расписание применяется в шахматных и шашечных турнирах быстрых игр, где игроки физически перемещаются вокруг стола. Во Франции это называется системой Карусель -Берже (Système Rutch-Berger). ^[13] ${\displaystyle (n-1)}$

Расписание также может быть использовано для «асинхронных» круговых турниров, где все игры проходят в разное время (например, потому что есть только одно место проведения). Игры проводятся слева направо в каждом раунде и с первого раунда до последнего. Когда количество участников четное, это расписание хорошо работает в отношении показателей качества и справедливости, таких как количество отдыха между играми. С другой стороны, когда количество участников нечетное, оно не так хорошо работает, и другое расписание лучше в отношении этих показателей. ^[14]

столы Бергера

В качестве альтернативы таблицы Бергера, ^[15] названные в честь австрийского мастера шахмат Иоганна Бергера , широко используются при планировании турниров. ^[16] Бергер опубликовал таблицы жеребьёвки в своих двух Schach-Jahrbücher (Шахматные анналы), ^{[17] [18]} со ссылкой на их изобретателя Рихарда Шурига. ^{[19] [20]}

Это составляет расписание, в котором игрок 14 имеет фиксированную позицию, а все остальные игроки вращаются против часовой стрелки . Это расписание легко генерируется вручную. Чтобы построить следующий раунд, последний игрок, номер 8 в первом раунде, перемещается во главу таблицы, за ним следует игрок 9 против игрока 7, игрок 10 против 6, пока игрок 1 против игрока 2. Арифметически это равносильно добавлению к предыдущей строке, за исключением игрока . Когда результат сложения больше , то вычтите из суммы. ${\displaystyle {\frac {n}{2}}}$ ${\displaystyle {\frac {n}{2}}}$ ${\displaystyle n}$ ${\displaystyle (n-1)}$ ${\displaystyle (n-1)}$

Это расписание также можно представить в виде таблицы (n-1, n-1), выражающей раунд, в котором игроки встречаются друг с другом. Например, игрок 7 играет против игрока 11 в раунде 4. Если игрок встречается сам с собой, то это показывает пропуск или игру против игрока n. Все игры в раунде составляют диагональ в таблице.

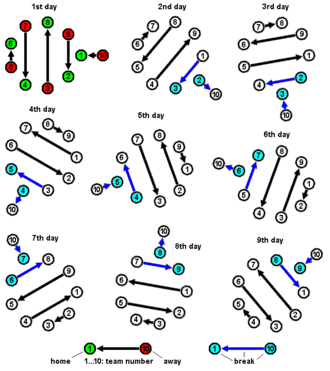
Приведенный выше график также можно представить в виде графика, как показано ниже:

Круговой Робин График Диаграмма Протяженности

И график, и расписание были представлены Эдуардом Люка в ^[21] как развлекательная математическая головоломка. Лукас, который описывает метод как простой и гениальный , приписывает решение Феликсу Валецкому, учителю лицея Кондорсе . Лукас также включил альтернативное решение с помощью скользящей головоломки .

Мнемонический

Чтобы легко запомнить этот метод, можно использовать следующую мнемонику. Начиная с первого раунда,

 место проведения = 1  ╭────────────────────────────────────────────────── ───┐1—ω >>> 2—13 >>> 3—12 >>> 4—11 >>> 5—10 >>> 6—9 >>> 7—8

строится следующий раунд:

ω—8 >>> 9—7 >>> 10—6 >>> 11—5 >>> 12—4 >>> 13—3 >>> 1—2

а потом,

2—ω >>> 3—1 >>> 4—13 >>> 5—12 >>> 6—11 >>> 7—10 >>> 8—9ω—9 >>> ...

Если количество игроков нечетное, игрок на первом месте получает пропуск. Если количество четное, дополнительный игрок (ω) становится противником.

Оригинальная конструкция таблиц сопряжения Рихарда Шурига (1886)

Для четного или нечетного числа участников Шуриг ^[20] строит таблицу с вертикальными и горизонтальными рядами. Затем он заполняет ее, начиная с верхнего левого угла, повторяя последовательность чисел от 1 до . Вот пример таблицы для 7 или 8 участников: ${\displaystyle n}$ ${\displaystyle n-1}$ ${\displaystyle n/2}$ ${\displaystyle n-1}$ ${\displaystyle n-1}$

Затем для получения противников строится вторая таблица. Каждая горизонтальная строка заполняется теми же числами, что и строка в предыдущей таблице (последняя строка заполняется числами из первой строки в исходной таблице), но в обратном порядке (справа налево). ${\displaystyle x}$ ${\displaystyle x+1}$

Объединив приведенные выше таблицы:

Затем обновляется первый столбец: если количество участников четное, номер игрока попеременно заменяется на первую и вторую позиции, а если количество участников нечетное, то вместо этого используется свободный номер. ${\displaystyle n}$

Таблицы пар были опубликованы в качестве приложения к порядку проведения мастер-турниров. Шуриг не предоставил доказательств или мотивации для своего алгоритма. ^[22]

Смотрите также

• Система рейтинга группового турнира , включая детали систем определения победителей
• Комбинаторный дизайн , сбалансированный турнирный дизайн порядка n (a BTD( n ))
• Турнир (теория графов) , математическая модель кругового турнира
• Турнир по системе Макмахона , разновидность швейцарской системы, которая включает в себя предварительные рейтинги для предотвращения раннего неравномерного распределения пар.
• Система плей-офф Шонесси , тип турнира с выбыванием из одного матча, в котором участвуют четыре команды.
• Система Макинтайра , серия форматов турниров, сочетающих черты турниров с выбыванием по системе Single-Alignment и Double Elimination.
• Двойные движения моста
• Список круговых шахматных турниров
• Система Схевенингена , где каждый член одной команды играет с каждым членом другой
• Метод Коупленда
• Метод Кондорсе
• критерий Кондорсе
• Три очка за победу , для круговой системы последствия различных систем подсчета очков

Ссылки

1. Третий новый международный словарь английского языка Вебстера, несокращенный (1971, G. & C. Merriam Co), стр. 1980.
2. Оркатт, Уильям Дана (1895). Официальный бюллетень лаун-тенниса. Том 2. Нью-Йорк: The Editors. С. 1, 3.
3. Стрелов, Ричард А.; Райт, Сью Эллен, ред. (1993). Стандартизация терминологии для лучшей коммуникации: практика, прикладная теория и результаты . Том 1166. ASTM. стр. 336–337. ISBN 0-8031-1493-1.
4. Словарь фраз и басен Брюэра . Нью-Йорк: Harper & Brother Publishers. С. 786.
5. «Словарь терминов, используемых в связи с бильярдом». Billiard Monthly . Английская ассоциация любителей бильярда. Февраль 1912 г. Архивировано из оригинала 3 марта 2022 г. Американский турнир: турнир, в котором каждый игрок должен по очереди встретиться с каждым другим игроком.
6. Allied. "Американский турнир". Chambers 21st Century Dictionary . Allied Publishers. стр. 38. ISBN 978-0550106254. Получено 1 августа 2012 г. .
7. Мид, Шепард (1977). Как добиться успеха в теннисе, не прилагая особых усилий: простой теннисный способ делать все, чему вас не научит ни один теннисный профессионал. Маккей. С. 130. ISBN 9780679507499. Получено 1 августа 2012 г. .
8. "Введение в турниры с рейтингом USCF" (PDF) . Федерация шахмат США . 23 февраля 2006 г. Архивировано (PDF) из оригинала 23 февраля 2022 г.
9. "Сыграет ли Индия в Кубке чемпионов ICC в Пакистане: капитан Рохит Шарма нарушает молчание". The Week . Получено 10 ноября 2024 г. .
10. "Восемь олимпийских игроков в бадминтон дисквалифицированы за "бросковые игры"". The Guardian . 1 августа 2012 г. Получено 1 августа 2012 г.
11. «UC Berkeley Quiz Bowl: Как составлять расписания». www.ocf.berkeley.edu .
12. Диниц, Джефф (13 ноября 2004 г.). «Разработка расписаний для лиг и турниров» (PDF) . Домашняя страница Джеффа Диница . Колледж Маунт-Сент-Мэри: ТЕОРИЯ ГРАФОВ, ДЕНЬ 48. Архивировано (PDF) из оригинала 23 февраля 2022 г.
13. Le livre de l'arbrere: издание 2008 г. (PDF) (на французском языке). Французская федерация образования. 2008. с. 56. ИСБН 978-2-915853-01-8. Архивировано (PDF) из оригинала 19 января 2013 г.
14. Suksompong, Warut (2016). «Планирование асинхронных круговых турниров». Operations Research Letters . 44 (1): 96–100. arXiv : 1804.04504 . doi : 10.1016/j.orl.2015.12.008. S2CID  4931332.
15. Таблица Берже (на французском) , примеры графиков круговых соревнований с участием до 30 человек.
16. "C. Общие правила и технические рекомендации для турниров / 05. Общие положения для соревнований / Общие положения для соревнований. Приложение 1: Детали таблицы Бергера /". Справочник ФИДЕ. ФИДЕ.(страница содержания)
17. Бергер, Иоганн (1893). Шах-Ярбух для 1892/93 г. (на немецком языке). Лейпциг. стр. 26–31. ОСЛК  651254787.{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
18. Бергер, Иоганн (1899). Schach-Jahrbuch für 1899/1900: Fortsetzung des Schach-Jahrbuches für 1892/93 (на немецком языке). Лейпциг. стр. 21–27. ОСЛК  651254792.{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
19. Ричард Шуриг (на французском)
20. Шуриг, Ричард (1886). «Die Paarung der Theilnehmer eines Turniers». Deutsche Schachzeitung (на немецком языке). 41 : 134–137. OCLC  556959107.Deutsche Schachzeitung в цифровой библиотеке HathiTrust
21. Лукас, Эдуард (1883). «Игры девиц». Récréations Mathématiques (на французском языке). Париж: Готье-Виллар. стр. 161–197.
22. Аренс, Вильгельм (1901). «XIV Anordnungs Issuee, § 1 Anordnungen im Kreise, Aufgabe 2». Mathematische Unterhaltungen und Spiele (на немецком языке). Лейпциг: Б. Г. Тойбнер. стр. 259–272. ковчег:/13960/t2w37mv93.