Потенциальная яма — это область, окружающая локальный минимум потенциальной энергии . Энергия, захваченная в потенциальной яме, не может преобразоваться в другой тип энергии ( кинетическую энергию в случае гравитационной потенциальной ямы), поскольку она захвачена в локальном минимуме потенциальной ямы. Следовательно, тело не может перейти к глобальному минимуму потенциальной энергии, как это было бы естественно из-за энтропии .
Энергия может быть высвобождена из потенциальной ямы, если в систему добавлено достаточно энергии, чтобы преодолеть локальный максимум. В квантовой физике потенциальная энергия может покинуть потенциальную яму без добавления энергии из-за вероятностных характеристик квантовых частиц ; в этих случаях можно представить, что частица туннелирует сквозь стенки потенциальной ямы.
График функции потенциальной энергии 2D представляет собой поверхность потенциальной энергии , которую можно представить как поверхность Земли в ландшафте холмов и долин. Тогда потенциальная яма будет долиной, окруженной со всех сторон возвышенностями, которые, таким образом, могут быть заполнены водой (например, быть озером ) без оттока воды к другому, более низкому минимуму (например, уровню моря ).
В случае гравитации область вокруг массы представляет собой гравитационную потенциальную яму, если только плотность массы не настолько мала, что приливные силы от других масс превышают силу тяжести самого тела.
Потенциальный холм — это противоположность потенциальной ямы, и представляет собой область, окружающую локальный максимум .
Квантовое ограничение можно наблюдать, когда диаметр материала имеет ту же величину, что и длина волны де Бройля волновой функции электрона . [1] Когда материалы настолько малы, их электронные и оптические свойства существенно отличаются от свойств объемных материалов. [2]
Частица ведет себя так, как будто она свободна, когда ограничивающее измерение велико по сравнению с длиной волны частицы. В этом состоянии запрещенная зона остается на своем первоначальном уровне энергии из-за непрерывного энергетического состояния. Однако, когда ограничивающее измерение уменьшается и достигает определенного предела, обычно в наномасштабе, энергетический спектр становится дискретным . В результате запрещенная зона становится зависимой от размера. По мере уменьшения размера частиц электроны и электронные дырки сближаются, и энергия, необходимая для их активации, увеличивается, что в конечном итоге приводит к синему смещению в излучении света .
В частности, эффект описывает явление, возникающее в результате сжатия электронов и электронных дырок в измерение, приближающееся к критическому квантовому измерению, называемому радиусом Бора экситона . В текущем применении квантовая точка, такая как небольшая сфера, ограничивает в трех измерениях, квантовая проволока ограничивает в двух измерениях, а квантовая яма ограничивает только в одном измерении. Они также известны как нуль-, одно- и двумерные потенциальные ямы соответственно. В этих случаях они относятся к числу измерений, в которых ограниченная частица может действовать как свободный носитель. См. внешние ссылки ниже для примеров применения в биотехнологии и технологии солнечных батарей.
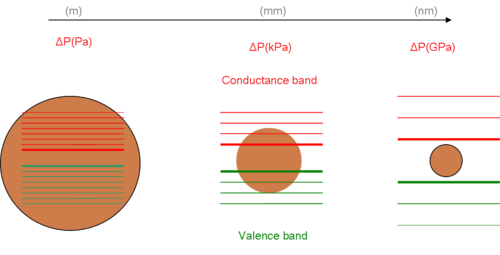
Электронные и оптические свойства материалов зависят от размера и формы. Хорошо зарекомендовавшие себя технические достижения, включая квантовые точки, были получены из манипуляции размером и исследования для их теоретического подтверждения эффекта квантового ограничения. [3] Основная часть теории заключается в том, что поведение экситона напоминает поведение атома, когда окружающее его пространство сокращается. Довольно хорошим приближением поведения экситона является трехмерная модель частицы в ящике . [4] Решение этой проблемы дает единственную [ необходимо разъяснение ] математическую связь между энергетическими состояниями и размерностью пространства. Уменьшение объема или размеров доступного пространства увеличивает энергию состояний. На диаграмме показано изменение уровня энергии электрона и ширины запрещенной зоны между наноматериалом и его объемным состоянием.
Следующее уравнение показывает связь между уровнем энергии и расстоянием между измерениями:
Результаты исследований [5] дают альтернативное объяснение сдвига свойств в наномасштабе. В объемной фазе поверхности, по-видимому, контролируют некоторые макроскопически наблюдаемые свойства. Однако в наночастицах поверхностные молекулы не подчиняются ожидаемой конфигурации [ какой? ] в пространстве. В результате поверхностное натяжение изменяется колоссально.
Уравнение Юнга–Лапласа может дать основу для исследования масштаба сил, приложенных к поверхностным молекулам:
При предположении сферической формы и решении уравнения Юнга-Лапласа для новых радиусов (нм) мы оцениваем новый (ГПа). Чем меньше радиусы, тем больше давление. Увеличение давления в наномасштабе приводит к появлению сильных сил, направленных внутрь частицы. Следовательно, молекулярная структура частицы, по-видимому, отличается от объемной моды, особенно на поверхности. Эти аномалии на поверхности ответственны за изменения межатомных взаимодействий и запрещенной зоны . [6] [7]
![{\displaystyle E_{n_{x},n_{y},n_{z}}={\frac {\hbar ^{2}\pi ^{2}}{2m}}\left[\left({\frac {n_{x}}{L_{x}}}\right)^{2}+\left({\frac {n_{y}}{L_{y}}}\right)^{2}+\left({\frac {n_{z}}{L_{z}}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf75ae87451865b306158f067de13885bf5985ea)
