Правило наследования

Теория вероятности

В теории вероятностей правило последовательности — это формула, введенная в XVIII веке Пьером-Симоном Лапласом в ходе рассмотрения проблемы восхода Солнца . ^[1] Формула до сих пор используется, особенно для оценки основных вероятностей, когда имеется мало наблюдений или событий, которые вообще не наблюдались в (конечных) выборочных данных.

Заявление о правиле наследования

Если мы повторим эксперимент, который, как мы знаем, может привести к успеху или неудаче, n раз независимо, и получим s успехов и n - s неудач, то какова вероятность того, что следующее повторение будет успешным?

Более абстрактно: если X ₁ , ..., X _{n +1} являются условно независимыми случайными величинами , каждая из которых может принимать значение 0 или 1, то, если мы о них больше ничего не знаем,

${\displaystyle P(X_{n+1}=1\mid X_{1}+\cdots +X_{n}=s)={s+1 \over n+2}.}$

Интерпретация

Поскольку мы заранее знаем, что рассматриваем эксперимент, для которого возможен как успех, так и неудача, наша оценка такова, как если бы мы наверняка наблюдали один успех и одну неудачу еще до того, как начали эксперименты. В каком-то смысле мы сделали n  + 2 наблюдения (известные как псевдоподсчеты ) с s  + 1 успехом. Хотя это может показаться самым простым и разумным предположением, которое также оказывается верным, оно все же требует доказательства. Действительно, предположение о том, что псевдосчетчик равен одному на каждую возможность, является одним из способов обобщения двоичного результата, но имеет неожиданные последствия — см. Обобщение на любое количество возможностей ниже.

Тем не менее, если бы мы с самого начала не знали, что возможны как успех, так и неудача, нам пришлось бы приписать

${\displaystyle P'(X_{n+1}=1\mid X_{1}+\cdots +X_{n}=s)={s \over n}.}$

Но см. «Математические детали» ниже для анализа его обоснованности. В частности, это недействительно, когда , или . ${\displaystyle s=0}$ ${\displaystyle s=n}$

Если количество наблюдений увеличивается и становится все более похожим, что интуитивно понятно: чем больше у нас данных, тем меньшее значение следует придавать нашей предшествующей информации. ${\displaystyle P}$ ${\displaystyle P'}$

Историческое применение к проблеме восхода солнца

Лаплас использовал правило последовательности, чтобы вычислить вероятность того, что Солнце взойдет завтра, учитывая, что оно восходило каждый день в течение последних 5000 лет. Получается очень большой коэффициент, примерно 5000 × 365,25, что дает шансы примерно 1 826 200 к 1 в пользу того, что Солнце взойдет завтра.

Однако, как показывают приведенные ниже математические детали, основным предположением для использования правила последовательности будет то, что у нас нет предварительных знаний о том, взойдет или не взойдет Солнце завтра, за исключением того, что оно может сделать и то, и другое. Это не относится к восходам солнца.

Лаплас это хорошо знал и в заключение примера с восходом солнца написал: «Но это число гораздо больше для того, кто, видя в совокупности явлений принцип, регулирующий дни и времена года, сознает, что ничто в настоящий момент не может остановить течение». этого». ^[2] Однако за этот расчет Лапласа высмеивали; его оппоненты ^{[ кто? ]} не обратил внимания на это предложение или не понял его важности. ^[2]

В 1940-х годах Рудольф Карнап исследовал вероятностную теорию индуктивного рассуждения и разработал меры степени подтверждения, которые он рассматривал как альтернативу правилу преемственности Лапласа. ^{[3] [4]} См. также Новая загадка индукции#Карнап .

Интуиция

Точка Z — это нулевая точка, P — это точка, в которой доля окружности от Z до P (синим цветом) равна p . Значение p — это в точности количество синих дуг, деленное на общее количество дуг. Если мы позволим первой точке дуги по часовой стрелке определять ее, то каждая точка на круге определяет одну дугу, причем Z определяет синюю дугу, а P определяет не синюю дугу. Тогда оценка p на одну ( Z ) больше, чем синие точки, деленная на два ( Z и P ), больше общего количества испытаний, что является правилом последовательности.

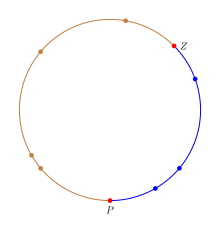
Правило последовательности можно интерпретировать интуитивно, рассматривая точки, случайно распределенные по кругу, а не подсчитывая количество «успехов»/«неуспехов» в эксперименте. ^[5] Чтобы имитировать поведение пропорции p на круге, мы раскрасим круг в два цвета, и доля круга, окрашенная в цвет «успеха», будет равна p . Чтобы выразить неопределенность относительно значения p , нам нужно выбрать часть круга.

Дробь выбирается путем выбора двух равномерно случайных точек на окружности. Первая точка Z соответствует нулю в интервале [0, 1], а вторая точка P соответствует p в интервале [0, 1]. В терминах круга доля круга от Z до P , движущаяся по часовой стрелке, будет равна p . n испытаний можно интерпретировать как n точек, равномерно распределенных по кругу; любая точка в дроби «успеха» является успехом, а в противном случае — неудачей. Это обеспечивает точное отображение успешных/неудачных экспериментов с вероятностью успеха p на равномерно случайные точки на круге. На рисунке доля успеха окрашена в синий цвет, чтобы отличать ее от остального круга, а точки P и Z выделены красным.

Учитывая этот круг, оценка p — это доля, окрашенная в синий цвет. Давайте разделим круг на n+2 дуги, соответствующие n+2 точкам, так что участок от точки на круге до следующей точки (движение по часовой стрелке) будет одной дугой, связанной с первой точкой. Таким образом, Z определяет первую синюю дугу, а P определяет первую не синюю дугу/дугу отказа. Поскольку следующая точка является равномерно случайной точкой, если она попадает в любую из синих дуг, испытание завершается успешно, а если она попадает в любую из других дуг, то оно терпит неудачу. Таким образом, вероятность успеха p равна где b — количество синих дуг, а t — общее количество дуг. Обратите внимание, что существует на одну синюю дугу (у Z ) больше, чем у точки успеха, и на две дуги (у P и Z ) больше, чем у n точек. Замена значений количеством успехов дает правило преемственности. ${\displaystyle {\frac {b}{t}}}$

Примечание. Для фактической вероятности необходимо использовать длину синих дуг, разделенную на длину всех дуг. Однако когда k точек равномерно и случайно распределены по окружности, расстояние от точки до следующей точки равно 1/k. Таким образом, в среднем каждая дуга имеет одинаковую длину, и соотношение длин становится соотношением отсчетов.

Математические детали

Пропорции p присваивается равномерное распределение, чтобы описать неопределенность относительно ее истинного значения. (Эта пропорция не случайна, а неопределенна. Мы присваиваем p распределение вероятностей , чтобы выразить нашу неопределенность, а не приписываем  p случайность . Но с математической точки зрения это равнозначно тому же, что рассматривать p как если бы оно было случайным).

Пусть X _i будет 1, если мы наблюдаем «успех» в i- м испытании , в противном случае 0, с вероятностью p успеха в каждом испытании. Таким образом, каждый X равен 0 или 1; каждый X имеет распределение Бернулли . Предположим, что эти X условно независимы при заданном p .

Мы можем использовать теорему Байеса , чтобы найти условное распределение вероятностей p с учетом данных X _i , i = 1, ..., n. Для « априорной » (т. е. маргинальной) вероятностной меры p мы назначили равномерное распределение на открытом интервале (0,1)

${\displaystyle f(p)={\begin{cases}0&{\text{for }}p\leq 0\\1&{\text{for }}0<p<1\\0&{\text{for }}p\geq 1\end{cases}}}$

Для вероятности данного p при наших наблюдениях мы используем функцию правдоподобия

${\displaystyle L(p)=P(X_{1}=x_{1},\ldots ,X_{n}=x_{n}\mid p)=\prod _{i=1}^{n}p^{x_{i}}(1-p)^{1-x_{i}}=p^{s}(1-p)^{n-s}}$

где s  =  x ₁  + ... +  x _n — количество «успехов», а n — количество испытаний (мы используем заглавную букву X для обозначения случайной величины и строчную букву x для фактически наблюдаемых данных). Собрав все это вместе, мы можем вычислить апостериорную величину:

${\displaystyle f(p\mid X_{1}=x_{1},\ldots ,X_{n}=x_{n})={L(p)f(p) \over \int _{0}^{1}L(r)f(r)\,dr}={p^{s}(1-p)^{n-s} \over \int _{0}^{1}r^{s}(1-r)^{n-s}\,dr}}$

Чтобы получить нормировочную константу , находим

${\displaystyle \int _{0}^{1}r^{s}(1-r)^{n-s}\,dr={s!(n-s)! \over (n+1)!}}$

( подробнее об интегралах этой формы см. в бета-функции ).

Таким образом, апостериорная функция плотности вероятности равна

${\displaystyle f(p\mid X_{1}=x_{1},\ldots ,X_{n}=x_{n})={(n+1)! \over s!(n-s)!}p^{s}(1-p)^{n-s}.}$

Это бета-распределение с ожидаемым значением

${\displaystyle \operatorname {E} (p\mid X_{i}=x_{i}{\text{ for }}i=1,\dots ,n)=\int _{0}^{1}pf(p\mid X_{1}=x_{1},\ldots ,X_{n}=x_{n})\,dp={s+1 \over n+2}.}$

Поскольку p говорит нам о вероятности успеха в любом эксперименте, а каждый эксперимент условно независим , условная вероятность успеха в следующем эксперименте равна просто p . Поскольку p рассматривается как случайная величина , закон полной вероятности говорит нам, что ожидаемая вероятность успеха в следующем эксперименте — это всего лишь ожидаемое значение p . Поскольку p зависит от наблюдаемых данных X _i для i = 1,..., n , мы имеем

${\displaystyle P(X_{n+1}=1\mid X_{i}=x_{i}{\text{ for }}i=1,\dots ,n)=\operatorname {E} (p\mid X_{i}=x_{i}{\text{ for }}i=1,\dots ,n)={s+1 \over n+2}.}$

Тот же расчет можно выполнить с (неправильным) априорным значением , которое выражает полное незнание p , включая незнание вопроса, может ли эксперимент быть успешным или потерпеть неудачу. Этот несобственный априор равен 1/( p (1 −  p )) для 0 ≤  p  ≤ 1 и 0 в противном случае. ^[6] Если приведенный выше расчет повторить с этим априором, мы получим

${\displaystyle P'(X_{n+1}=1\mid X_{i}=x_{i}{\text{ for }}i=1,\dots ,n)={s \over n}.}$

Таким образом, если предварительно указать полное невежество, вероятность успеха определяется наблюдаемой частотой успеха. Однако апостериорное распределение, которое привело к этому результату, представляет собой распределение Beta( s , n  −  s ), которое не является правильным, когда s  =  n или s  = 0 (т. е. константа нормализации бесконечна, когда s  = 0 или s  =  n ). . Это означает, что мы не можем использовать эту форму апостериорного распределения для расчета вероятности успешного следующего наблюдения, когда s  = 0 или s  =  n . Это делает информацию, содержащуюся в правиле преемственности, более яркой: ее можно рассматривать как выражение предварительного предположения о том, что если выборка будет продолжаться бесконечно, мы в конечном итоге увидим по крайней мере один успех и по крайней мере одну неудачу в выборке. Приор, выражающий полное невежество, не предполагает этого знания.

Чтобы оценить случай «полного незнания», когда можно иметь дело с s  = 0 или s  =  n , мы сначала вернемся к гипергеометрическому распределению , обозначенному . Именно этот подход использован Джейнсом (2003). Бином можно вывести как предельную форму, при этом их соотношение остается фиксированным. Можно думать о количестве успехов в общей численности населения размером . ${\displaystyle \mathrm {Hyp} (s|N,n,S)}$ ${\displaystyle \mathrm {Bin} (r|n,p)}$ ${\displaystyle N,S\rightarrow \infty }$ ${\displaystyle p={S \over N}}$ ${\displaystyle S}$ ${\displaystyle N}$

Эквивалентом до является , с доменом . Работа с условием означает, что оценка эквивалентна оценке с последующим делением этой оценки на . Апостериорную часть можно представить как: ${\displaystyle {1 \over p(1-p)}}$ ${\displaystyle {1 \over S(N-S)}}$ ${\displaystyle 1\leq S\leq N-1}$ ${\displaystyle N}$ ${\displaystyle p}$ ${\displaystyle S}$ ${\displaystyle N}$ ${\displaystyle S}$

${\displaystyle P(S|N,n,s)\propto {1 \over S(N-S)}{S \choose s}{N-S \choose n-s}\propto {S!(N-S)! \over S(N-S)(S-s)!(N-S-[n-s])!}}$

И видно, что если s  =  n или s  = 0, то один из факториалов в числителе сокращается ровно на единицу в знаменателе. В случае s =  0 имеем:

${\displaystyle P(S|N,n,s=0)\propto {(N-S-1)! \over S(N-S-n)!}={\prod _{j=1}^{n-1}(N-S-j) \over S}}$

Добавление нормализующей константы, которая всегда конечна (поскольку в области апостериорных значений нет особенностей и имеется конечное число членов), дает:

${\displaystyle P(S|N,n,s=0)={\prod _{j=1}^{n-1}(N-S-j) \over S\sum _{R=1}^{N-n}{\prod _{j=1}^{n-1}(N-R-j) \over R}}}$

Итак, апостериорное ожидание для : ${\displaystyle p={S \over N}}$

${\displaystyle E\left({S \over N}|n,s=0,N\right)={1 \over N}\sum _{S=1}^{N-n}SP(S|N,n=1,s=0)={1 \over N}{\sum _{S=1}^{N-n}\prod _{j=1}^{n-1}(N-S-j) \over \sum _{R=1}^{N-n}{\prod _{j=1}^{n-1}(N-R-j) \over R}}}$

Приблизительное аналитическое выражение для больших N дается путем сначала аппроксимации члена произведения:

${\displaystyle \prod _{j=1}^{n-1}(N-R-j)\approx (N-R)^{n-1}}$

а затем заменив сумму в числителе интегралом

${\displaystyle \sum _{S=1}^{N-n}\prod _{j=1}^{n-1}(N-S-j)\approx \int _{1}^{N-n}(N-S)^{n-1}\,dS={(N-1)^{n}-n^{n} \over n}\approx {N^{n} \over n}}$

Та же процедура применяется и для знаменателя, но процесс немного сложнее, так как интеграл сложнее вычислить.

${\displaystyle {\begin{aligned}\sum _{R=1}^{N-n}{\prod _{j=1}^{n-1}(N-R-j) \over R}&\approx \int _{1}^{N-n}{(N-R)^{n-1} \over R}\,dR\\&=N\int _{1}^{N-n}{(N-R)^{n-2} \over R}\,dR-\int _{1}^{N-n}(N-R)^{n-2}\,dR\\&=N^{n-1}\left[\int _{1}^{N-n}{dR \over R}-{1 \over n-1}+O\left({1 \over N}\right)\right]\approx N^{n-1}\ln(N)\end{aligned}}}$

где ln — натуральный логарифм, подстановка этих приближений в математическое ожидание дает

${\displaystyle E\left({S \over N}|n,s=0,N\right)\approx {1 \over N}{{N^{n} \over n} \over N^{n-1}\ln(N)}={1 \over n[\ln(N)]}={\log _{10}(e) \over n[\log _{10}(N)]}={0.434294 \over n[\log _{10}(N)]}}$

где в окончательном ответе для простоты вычислений использовался логарифм по основанию 10 . Например, если размер популяции составляет 10 ^тыс. , то вероятность успеха в следующей выборке определяется выражением:

${\displaystyle E\left({S \over N}\mid n,s=0,N=10^{k}\right)\approx {0.434294 \over nk}}$

Так, например, если население составляет порядка десятков миллиардов, так что k  = 10, и мы наблюдаем  безуспешные результаты n = 10, то ожидаемая доля в популяции составляет примерно 0,43%. Если популяция меньше, так что n  = 10, k  = 5 (десятки тысяч), ожидаемая доля возрастает примерно до 0,86% и так далее. Аналогично, если количество наблюдений меньше, так что n  = 5, k  = 10, пропорция снова возрастает примерно до 0,86%.

Эта вероятность не имеет положительной нижней границы и может быть сделана сколь угодно малой для все большего и большего выбора N или k . Это означает, что вероятность зависит от размера генеральной совокупности, из которой производится выборка. Переходя к пределу бесконечного N (для более простых аналитических свойств), мы «выбрасываем» часть очень важной информации. Обратите внимание, что это соотношение незнания сохраняется только до тех пор, пока не наблюдается никаких успехов. Соответственно, оно возвращается к наблюдаемому правилу частоты, как только наблюдается один успех. Соответствующие результаты получены для случая s=n путем переключения меток и последующего вычитания вероятности из 1. ${\displaystyle p={s \over n}}$

Обобщение на любое количество возможностей

В этом разделе дается эвристический вывод, аналогичный тому, который приведен в «Теории вероятностей: логика науки» . ^[7]

Правило преемственности имеет множество различных интуитивных интерпретаций, и в зависимости от того, какую интуицию использовать, обобщение может быть различным. Таким образом, отсюда следует действовать очень осторожно и заново выводить результаты из основных принципов, а не вводить интуитивно разумное обобщение. Полный вывод можно найти в книге Джейнса, но альтернативный вывод становится легче понять, если известно решение. Еще один момент, который следует подчеркнуть, заключается в том, что предшествующее состояние знаний, описываемое правилом последовательности, дается в виде перечисления возможностей с дополнительной информацией, которую можно наблюдать по каждой категории. Это можно эквивалентно однократному наблюдению за каждой категорией перед сбором данных. Чтобы обозначить, что это используемые знания, I _m ставится как часть условий в вероятностных заданиях.

Правило преемственности основано на установке биномиальной вероятности и равномерного предварительного распределения. Таким образом, прямое обобщение — это всего лишь многомерное расширение этих двух распределений: 1) установка равномерного априора для исходных m категорий и 2) использование полиномиального распределения в качестве функции правдоподобия (которое является многомерным обобщением биномиального распределения). Можно показать, что равномерное распределение является частным случаем распределения Дирихле со всеми его параметрами, равными 1 (точно так же, как равномерное распределение представляет собой бета(1,1) в двоичном случае). Распределение Дирихле является априорным для полиномиального распределения, что означает, что апостериорное распределение также является распределением Дирихле с другими параметрами. Пусть pi _{обозначает} вероятность того, что категория i будет наблюдаться, и пусть n _i обозначает количество раз, когда категория i ( i  = 1, ...,  m ) действительно наблюдалась. Тогда совместное апостериорное распределение вероятностей p ₁ , ...,  _pm определяется выражением:

${\displaystyle f(p_{1},\ldots ,p_{m}\mid n_{1},\ldots ,n_{m},I)={\begin{cases}{\displaystyle {\frac {\Gamma \left(\sum _{i=1}^{m}(n_{i}+1)\right)}{\prod _{i=1}^{m}\Gamma (n_{i}+1)}}p_{1}^{n_{1}}\cdots p_{m}^{n_{m}}},\quad &\sum _{i=1}^{m}p_{i}=1\\\\0&{\text{otherwise.}}\end{cases}}}$

Чтобы получить обобщенное правило последовательности, обратите внимание, что вероятность наблюдения категории i при следующем наблюдении, зависящая от pi _, равна просто pi _, нам просто нужно ее математическое ожидание. Обозначим A _i событие, когда следующее наблюдение относится к категории i ( i  = 1, ...,  m ), и пусть n  =  n ₁  + ... +  n _m будет общим количеством сделанных наблюдений. Результат, используя свойства распределения Дирихле:

${\displaystyle P(A_{i}|n_{1},\ldots ,n_{m},I_{m})={n_{i}+1 \over n+m}.}$

Это решение сводится к вероятности, которая будет назначена с использованием принципа безразличия до того, как будут сделаны какие-либо наблюдения (т. е. n  = 0), в соответствии с исходным правилом последовательности. Он также содержит правило преемственности как частный случай, когда m  = 2, как и должно быть обобщением.

Поскольку предложения или события A _i являются взаимоисключающими, m категорий можно объединить в 2. Просто сложите вероятности A _i , соответствующие «успеху», чтобы получить вероятность успеха. Предположим, что это объединяет категории c как «успех» и категории mc как «неудача». Обозначим s сумму соответствующих значений n _i , которые были названы «успехом». Тогда вероятность «успеха» в следующем испытании равна:

${\displaystyle P({\text{success}}|n_{1},\ldots ,n_{m},I_{m})={s+c \over n+m},}$

что отличается от первоначального правила наследования. Но обратите внимание, что исходное правило последовательности основано на I ₂ , тогда как обобщение основано на I _m . Это означает, что информация, содержащаяся в I _m , отличается от содержащейся в I ₂ . Это указывает на то, что простое знание о более чем двух исходах, которые, как мы знаем, возможны, является важной информацией при сокращении этих категорий до двух. Это иллюстрирует тонкость описания априорной информации и то, почему важно указывать, какую априорную информацию использовать.

Дальнейший анализ

Очень важна хорошая модель (т. е. хороший компромисс между точностью и практичностью). Перефразируя Лапласа о проблеме восхода солнца : хотя у нас есть огромное количество образцов восхода Солнца, существуют гораздо лучшие модели Солнца, чем предположение о том, что оно имеет определенную вероятность восхода каждый день, например, просто имеет период полураспада.

При наличии хорошей модели лучше всего провести как можно больше наблюдений в зависимости от ожидаемой надежности предшествующих знаний, стоимости наблюдений, имеющегося времени и ресурсов, а также требуемой точности.

Одним из самых сложных аспектов правила наследования являются не математические формулы, а ответ на вопрос: когда применяется правило наследования? В разделе обобщения это было очень четко отмечено путем добавления в расчеты априорной информации I _m . Таким образом, когда все, что известно о явлении, это то, что до наблюдения каких-либо данных известно m возможных результатов, только тогда применяется правило последовательности. Если правило последовательности применяется в задачах, где оно неточно описывает предшествующее состояние знаний, то оно может дать противоречивые результаты. Это происходит не потому, что правило преемственности несовершенно, а потому, что оно фактически отвечает на другой вопрос, основанный на другой предварительной информации.

В принципе (см. правило Кромвеля ), вероятность (или псевдосчет) любой возможности не должна быть установлена ​​равной нулю, поскольку ничто в физическом мире не должно считаться строго невозможным (хотя это может быть) — даже если это противоречит всем наблюдениям и текущим теориям. . Действительно, правило Байеса абсолютно не учитывает наблюдение, вероятность которого ранее считалась нулевой — оно до сих пор объявляется невозможным. Однако рассмотрение только фиксированного набора возможностей является приемлемым путем, нужно просто помнить, что результаты зависят (или ограничиваются) рассматриваемым набором, а не каким-то «универсальным» набором. Фактически Ларри Бретхорст показывает, что включение возможности «чего-то еще» в пространство гипотез не влияет на относительные вероятности другой гипотезы — оно просто перенормирует их, чтобы в сумме получить значение меньше 1. ^[8] До тех пор, пока «что-то» «иначе» указано, функция правдоподобия, обусловленная этим «чем-то еще», неопределенна, ибо как определить ? Таким образом, никакое обновление априорной вероятности «чего-то еще» не может произойти, пока оно не будет определено более точно. ${\displaystyle Pr({\text{data}}|{\text{something else}},I)}$

Однако иногда остается спорным вопрос о том, должны ли предварительные знания влиять на относительные вероятности или также на общий вес предшествующих знаний по сравнению с фактическими наблюдениями. На этот вопрос нет однозначного ответа, поскольку это зависит от того, какие предварительные знания учитываются. Фактически, альтернативное априорное состояние знаний могло бы иметь вид: «Я определил m потенциальных категорий, но я уверен, что только одна из них возможна до наблюдения данных. Однако я не знаю, какая именно категория это». ." Математическим способом описания этого априора является распределение Дирихле со всеми параметрами, равными m ^-1 , которое затем дает в знаменателе псевдосчет 1 вместо m и добавляет псевдосчет m ^-1 к каждой категории. Это дает немного другую вероятность в двоичном случае . ${\displaystyle {\frac {s+0.5}{n+1}}}$

На оценку априорных вероятностей стоит тратить значительные усилия только тогда, когда они могут иметь значительный эффект. Они могут быть важны, когда наблюдений мало — особенно когда их настолько мало, что было мало наблюдений за некоторыми возможностями, например, за редким животным в данном регионе. Это также важно, когда имеется много наблюдений, когда считается, что ожидание должно быть сильно взвешено по сравнению с предыдущими оценками, несмотря на многие наблюдения об обратном, например, для колеса рулетки в уважаемом казино. В последнем случае, по крайней мере, некоторые из псевдосчетов могут оказаться очень большими. Они не всегда малы и поэтому вскоре перевешиваются реальными наблюдениями, как это часто предполагается. Однако, хотя и в крайнем случае, для повседневных целей предварительные знания обычно жизненно важны. Таким образом, большинство решений должны быть в некоторой степени субъективными (в зависимости от аналитика и используемого анализа).

Смотрите также

• Аддитивное сглаживание
• Оценка Кричевского–Трофимова
• Принцип безразличия

Рекомендации

1. Лаплас, Пьер-Симон (1814). Философское эссе о вероятностях. Париж: Курьер.
2. Часть II, раздел 18.6 Джейнса, ET и Бретхорста, GL (2003). Теория вероятностей: логика науки. Издательство Кембриджского университета. ISBN  978-0-521-59271-0
3. Рудольф Карнап (1945). «Об индуктивной логике» (PDF) . Философия науки . 12 (2): 72–97. дои : 10.1086/286851. S2CID  14481246.; здесь: стр.86, 97
4. Рудольф Карнап (1947). «О применении индуктивной логики» (PDF) . Философия и феноменологические исследования . 8 (1): 133–148. дои : 10.2307/2102920. JSTOR  2102920.; здесь: стр.145
5. Нейман, Эрик. «Элегантное доказательство правила преемственности Лапласа». Неожиданные ценности . Эрик Нейман . Проверено 13 апреля 2023 г.
6. http://www.stats.org.uk/priors/noninformative/Smith.pdf ^{[ пустой URL-адрес PDF ]}
7. Джейнс, ET (2003), Теория вероятностей: логика науки , Кембридж, Великобритания, издательство Кембриджского университета.
8. Бреттост, Г. Ларри (1988). Байесовский спектральный анализ и оценка параметров (PDF) (кандидатская диссертация). п. 55.