
В математическом исследовании клеточных автоматов Правило 90 представляет собой элементарный клеточный автомат, основанный на функции «исключающее или» . Он состоит из одномерного массива ячеек, каждая из которых может содержать значение 0 или 1. На каждом временном шаге все значения одновременно заменяются на XOR их двух соседних значений. [1] Мартин, Одлыжко и Вольфрам (1984) называют его «простейшим нетривиальным клеточным автоматом», [2] и он подробно описан в книге Стивена Вольфрама 2002 года « Новый вид науки» . [3]
При запуске с одной живой клетки Правило 90 имеет пространственно-временную диаграмму в форме треугольника Серпинского . Поведение любой другой конфигурации можно объяснить как суперпозицию копий этого шаблона, объединенных с помощью функции исключающего или . Любая конфигурация только с конечным числом ненулевых ячеек становится репликатором , который в конечном итоге заполняет массив своими копиями. Когда Правило 90 запускается со случайной начальной конфигурации, его конфигурация остается случайной на каждом временном шаге. Его пространственно-временная диаграмма образует множество треугольных «окон» разных размеров, шаблонов, которые формируются, когда последовательный ряд ячеек одновременно становится нулевым, а затем ячейки со значением 1 постепенно перемещаются в этот ряд с обоих концов.
Некоторые из самых ранних исследований Правила 90 были сделаны в связи с нерешенной проблемой в теории чисел , гипотезой Гилбрета , о разнице последовательных простых чисел . Это правило также связано с теорией чисел другим способом, через последовательность Гулда . Эта последовательность подсчитывает количество ненулевых клеток на каждом временном шаге после начала Правила 90 с одной живой клеткой. Ее значения являются степенями двойки , с показателями, равными количеству ненулевых цифр в двоичном представлении номера шага. Другие приложения Правила 90 включают дизайн гобеленов .
Каждая конфигурация Правила 90 имеет ровно четыре предшественника, другие конфигурации, которые формируют данную конфигурацию после одного шага. Поэтому, в отличие от многих других клеточных автоматов, таких как Игра жизни Конвея , Правило 90 не имеет Сада Эдема , конфигурации без предшественников. Оно дает пример клеточного автомата, который является сюръективным (каждая конфигурация имеет предшественника), но не инъективным (он имеет наборы из более чем одной конфигурации с одним и тем же преемником). Из теоремы о Саде Эдема следует , что Правило 90 локально инъективно (все конфигурации с одним и тем же преемником изменяются в бесконечном числе ячеек).

Правило 90 — это элементарный клеточный автомат . Это означает, что он состоит из одномерного массива ячеек, каждая из которых содержит одно двоичное значение, либо 0, либо 1. Присвоение значений всем ячейкам называется конфигурацией . Автомату задается начальная конфигурация, а затем он проходит через другие конфигурации в последовательности дискретных временных шагов. На каждом шаге все ячейки обновляются одновременно. Заранее заданное правило определяет новое значение каждой ячейки как функцию ее предыдущего значения и значений в двух соседних ячейках. Все ячейки подчиняются одному и тому же правилу, которое может быть задано либо как формула, либо как таблица правил, которая определяет новое значение для каждой возможной комбинации соседних значений. [1]
В случае Правила 90 новое значение каждой ячейки является исключающим или двух соседних значений. Эквивалентно, следующее состояние этого конкретного автомата регулируется следующей таблицей правил: [1]
Название Правила 90 происходит от двоично-десятичной записи Стивена Вольфрама для правил одномерного клеточного автомата. Чтобы вычислить запись для правила, объедините новые состояния в таблице правил в одно двоичное число и преобразуйте число в десятичное : 01011010 2 = 90 10 . [1] Правило 90 также называют автоматом Серпинского из-за характерной формы треугольника Серпинского , которую оно генерирует, [4] и клеточным автоматом Мартина–Одлыжко–Вольфрама после ранних исследований Оливье Мартина, Эндрю М. Одлыжко и Стивена Вольфрама (1984) по этому автомату. [5]
Конфигурация в Правиле 90 может быть разделена на два подмножества ячеек, которые не взаимодействуют друг с другом. Одно из этих двух подмножеств состоит из ячеек в четных позициях на четных временных шагах и ячеек в нечетных позициях на нечетных временных шагах. Другое подмножество состоит из ячеек в четных позициях на нечетных временных шагах и ячеек в нечетных позициях на четных временных шагах. Каждое из этих двух подмножеств можно рассматривать как клеточный автомат только с его половиной ячеек. [6] Правило для автомата в пределах каждого из этих подмножеств эквивалентно (за исключением сдвига на половину ячейки за временной шаг) другому элементарному клеточному автомату , Правилу 102 , в котором новое состояние каждой ячейки является исключающим или ее старого состояния и ее правого соседа. То есть поведение Правила 90 по сути такое же, как поведение двух чередующихся копий Правила 102. [7]
Правило 90 и Правило 102 называются аддитивными клеточными автоматами . Это означает, что если два начальных состояния объединяются путем вычисления исключающего или каждого из их состояний, то их последующие конфигурации будут объединены таким же образом. В более общем смысле, можно разбить любую конфигурацию Правила 90 на два подмножества с непересекающимися ненулевыми ячейками, развить два подмножества по отдельности и вычислить каждую последующую конфигурацию исходного автомата как исключающее или конфигураций на тех же временных шагах двух подмножеств. [2]
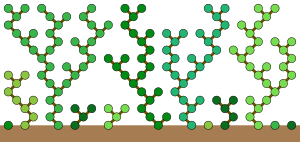
Автомат Правила 90 (в эквивалентной форме на одном из двух независимых подмножеств чередующихся ячеек) был исследован в начале 1970-х годов в попытке получить дополнительное представление о гипотезе Гилбрета о разностях последовательных простых чисел . В треугольнике чисел, сгенерированных из простых чисел путем многократного применения оператора прямой разности , оказывается, что большинство значений равны либо 0, либо 2. В частности, гипотеза Гилбрета утверждает, что самые левые значения в каждой строке этого треугольника равны либо 0, либо 2. Когда непрерывная подпоследовательность значений в одной строке треугольника равна либо 0, либо 2, то Правило 90 можно использовать для определения соответствующей подпоследовательности в следующей строке. Миллер (1970) объяснил правило метафорой роста деревьев в лесу, озаглавив свою статью на эту тему «Периодические леса низкорослых деревьев». В этой метафоре дерево начинает расти в каждой позиции начальной конфигурации, значение которой равно 1, и этот лес деревьев затем растет одновременно, на новую высоту над землей на каждом временном шаге. Каждая ненулевая ячейка на каждом временном шаге представляет позицию, которую занимает растущая ветвь дерева. На каждом последующем временном шаге ветвь может вырасти в одну из двух ячеек над ней слева и справа, только когда нет другой ветви, конкурирующей за ту же ячейку. Лес деревьев, растущий в соответствии с этими правилами, имеет точно такое же поведение, как и Правило 90. [8]
Из любой начальной конфигурации Правила 90 можно сформировать математический лес , направленный ациклический граф , в котором каждая вершина имеет не более одного исходящего ребра, чьи деревья такие же, как деревья в метафоре Миллера. Лес имеет вершину для каждой пары ( x , i ) такую, что ячейка x ненулевая в момент времени i . Вершины в момент времени 0 не имеют исходящих ребер; каждая из них образует корень дерева в лесу. Для каждой вершины ( x , i ) с i ненулевым, ее исходящее ребро идет к ( x ± 1, i − 1) , уникальному ненулевому соседу x на временном шаге i − 1 . Миллер заметил, что эти леса развивают треугольные «просеки», области диаграммы времени-пространства без ненулевых ячеек, ограниченные плоским нижним краем и диагональными сторонами. Такая поляна образуется, когда последовательная последовательность ячеек становится нулевой одновременно за один временной шаг, а затем (в метафоре дерева) ветви растут внутрь, в конечном итоге заново покрывая ячейки последовательности. [8]
Для случайных начальных условий границы между деревьями, сформированными таким образом, сами смещаются в, казалось бы, случайном порядке, и деревья часто вымирают вообще. Но с помощью теории регистров сдвига он и другие смогли найти начальные условия, при которых все деревья остаются живыми навсегда, схема роста периодически повторяется, и все поляны могут гарантированно оставаться ограниченными по размеру. [8] [9] Миллер использовал эти повторяющиеся узоры для формирования рисунков гобеленов . Некоторые из гобеленов Миллера изображают физические деревья; другие визуализируют автомат Правила 90 с помощью абстрактных узоров треугольников. [8]

Пространственно-временная диаграмма Правила 90 представляет собой график, в котором i -я строка записывает конфигурацию автомата на шаге i . Когда начальное состояние имеет одну ненулевую ячейку, эта диаграмма имеет вид треугольника Серпинского , фрактала, образованного путем объединения треугольников в более крупные треугольники. Правила 18, 22, 26, 82, 146, 154, 210 и 218 также генерируют треугольники Серпинского из одной ячейки, однако не все из них создаются полностью идентично. Один из способов объяснить эту структуру использует тот факт, что в Правиле 90 каждая ячейка является исключающим ИЛИ своих двух соседей. Поскольку это эквивалентно сложению по модулю -2, это генерирует версию треугольника Паскаля по модулю -2 . На диаграмме есть 1 везде, где треугольник Паскаля имеет нечетное число , и 0 везде, где треугольник Паскаля имеет четное число . Это дискретная версия треугольника Серпинского. [1] [10]
Число живых клеток в каждой строке этого шаблона является степенью двойки . В i -й строке оно равно 2k , где k — число ненулевых цифр в двоичном представлении числа i . Последовательность этих чисел живых клеток,
известна как последовательность Гулда . Единственная живая клетка начальной конфигурации представляет собой пилообразный узор . Это означает, что в некоторые временные интервалы число живых клеток увеличивается произвольно, в то время как в другие они возвращаются только к двум живым клеткам, бесконечно часто. Скорость роста этого узора имеет характерную форму растущей пилообразной волны , которая может быть использована для распознавания физических процессов, которые ведут себя подобно Правилу 90. [4]
Треугольник Серпинского также встречается более тонким образом в эволюции любой конфигурации в Правиле 90. На любом временном шаге i в эволюции Правила состояние любой ячейки может быть рассчитано как исключительное или подмножества ячеек в начальной конфигурации. Это подмножество имеет ту же форму, что и i -я строка треугольника Серпинского. [11]
В треугольнике Серпинского для любого целого числа i строки, пронумерованные кратно 2 i, имеют ненулевые ячейки, отстоящие друг от друга на расстояние не менее 2 i единиц. Поэтому, из-за аддитивного свойства правила 90, если начальная конфигурация состоит из конечного шаблона P ненулевых ячеек шириной менее 2 i , то на шагах, кратных 2 i , конфигурация будет состоять из копий P , отстоящих друг от друга на расстояние не менее 2 i единиц от начала до начала. Это расстояние достаточно велико, чтобы копии не мешали друг другу. Количество копий равно количеству ненулевых ячеек в соответствующей строке треугольника Серпинского. Таким образом, в этом правиле каждый шаблон является репликатором : он генерирует несколько своих копий, которые распространяются по конфигурации, в конечном итоге заполняя весь массив. Другие правила, включая универсальный конструктор Фон Неймана , клеточный автомат Кодда и циклы Лэнгтона, также имеют репликаторы, которые работают, перенося и копируя последовательность инструкций для построения самих себя. Напротив, репликация в правиле 90 тривиальна и автоматична. [12]
В правиле 90 на бесконечной одномерной решетке каждая конфигурация имеет ровно четыре конфигурации предшественников. Это происходит потому, что в предшественнике любые две последовательные ячейки могут иметь любую комбинацию состояний, но как только состояния этих двух ячеек выбраны, есть только один последовательный выбор для состояний оставшихся ячеек. Следовательно, в правиле 90 нет райского сада , конфигурации без предшественников. Конфигурация правила 90, состоящая из одной ненулевой ячейки (со всеми остальными ячейками нулевыми), не имеет предшественников, которые имеют конечное число ненулевых элементов. Однако эта конфигурация не является райским садом, потому что у нее есть предшественники с бесконечным числом ненулевых элементов. [13]
Тот факт, что каждая конфигурация имеет предшественника, можно обобщить, сказав, что Правило 90 является сюръективным . Функция, которая отображает каждую конфигурацию в ее последователя, является математически сюръективной функцией. Правило 90 также не является инъективным . В инъективном правиле каждые две различные конфигурации имеют различных последователей, но Правило 90 имеет пары конфигураций с одним и тем же последователем. Правило 90 дает пример клеточного автомата, который является сюръективным, но не инъективным. Теорема о Эдемском саду Мура и Майхилла подразумевает, что каждый инъективный клеточный автомат должен быть сюръективным, но этот пример показывает, что обратное неверно. [13] [14]
Поскольку каждая конфигурация имеет только ограниченное число предшественников, эволюция Правила 90 сохраняет энтропию любой конфигурации. В частности, если бесконечная начальная конфигурация выбирается путем выбора состояния каждой ячейки независимо случайным образом, причем каждое из двух состояний имеет одинаковую вероятность быть выбранным, то каждая последующая конфигурация может быть описана точно таким же распределением вероятностей. [2]
Многие другие клеточные автоматы и другие вычислительные системы способны эмулировать поведение Правила 90. Например, конфигурация в правиле 90 может быть переведена в конфигурацию в другом элементарном клеточном автомате Правило 22. Трансляция заменяет каждую ячейку Правила 90 тремя последовательными ячейками Правила 22. Все эти ячейки равны нулю, если ячейка Правила 90 сама равна нулю. Ненулевая ячейка Правила 90 транслируется в единицу, за которой следуют два нуля. При таком преобразовании каждые шесть шагов автомата Правила 22 имитируют один шаг автомата Правила 90. Аналогичные прямые симуляции Правила 90 также возможны для элементарных клеточных автоматов Правила 45 и Правила 126, для определенных систем перезаписи строк и систем тегов , а также в некоторых двумерных клеточных автоматах, включая Wireworld . Правило 90 также может имитировать себя таким же образом. Если каждую ячейку конфигурации Правила 90 заменить парой последовательных ячеек, первая из которых содержит значение исходной ячейки, а вторая — ноль, то эта удвоенная конфигурация будет вести себя так же, как и исходная конфигурация, но на половинной скорости. [15]
Известно, что различные другие клеточные автоматы поддерживают репликаторы, шаблоны, которые копируют себя, и большинство из них ведут себя так же, как в модели роста дерева для Правила 90. Новая копия помещается по обе стороны шаблона репликатора, пока пространство там пусто. Однако, если два репликатора оба пытаются скопировать себя в одну и ту же позицию, то пространство остается пустым. В любом случае сами репликаторы исчезают, оставляя свои копии для продолжения репликации. Стандартным примером такого поведения является шаблон «паста-бабочка» в двумерном правиле HighLife . Это правило ведет себя во многом как игра Конвея «Жизнь», но такого маленького репликатора в Жизни не существует. Всякий раз, когда автомат поддерживает репликаторы с той же моделью роста, одномерные массивы репликаторов могут быть использованы для моделирования Правила 90. [16] Правило 90 (на конечных рядах клеток) также может быть смоделировано блочными осцилляторами двумерного клеточного автомата, подобного жизни B36/S125, также называемого «2x2», и поведение Правила 90 может быть использовано для характеристики возможных периодов этих осцилляторов. [17]