Призматический

Многогранник со всеми вершинами в двух параллельных плоскостях

Призматоид с параллельными гранями A ₁ и A ₃ , срединным сечением A ₂ и высотой h

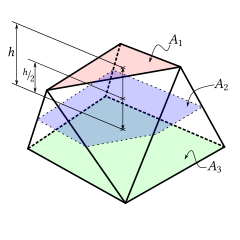
В геометрии призматоид — это многогранник , все вершины которого лежат в двух параллельных плоскостях . Его боковые грани могут быть трапециями или треугольниками . ^[1] Если обе плоскости имеют одинаковое количество вершин, а боковые грани являются либо параллелограммами , либо трапециями, то он называется призмоидом . ^[2]

Объем

_Если площади двух параллельных граней равны A1 и A3 , площадь поперечного сечения призматоида с плоскостью, расположенной посередине между двумя параллельными гранями, равна _{A2 ,} а высота (расстояние между двумя параллельными гранями) равна h , то объем призматоида определяется выражением ^[3]. Эта формула немедленно получается путем интегрирования площади, параллельной двум плоскостям вершин, по правилу Симпсона , поскольку это правило является точным для интегрирования многочленов степени до 3, и в этом случае площадь является не более чем квадратичной функцией высоты. $${\displaystyle V={\frac {h(A_{1}+4A_{2}+A_{3})}{6}}.}$$

Призматические семейства

Семейства призматоидов включают:

• Пирамиды , в которых одна плоскость содержит только одну точку;
• Клинья , в которых одна плоскость содержит только две точки;
• Призмы , многоугольники которых в каждой плоскости равны и соединены прямоугольниками или параллелограммами;
• Антипризмы , многоугольники которых в каждой плоскости конгруэнтны и соединены чередующейся полосой треугольников;
• Звездные антипризмы ;
• Купола , в которых многоугольник в одной плоскости содержит в два раза больше точек, чем в другой, и соединен с ней чередующимися треугольниками и прямоугольниками;
• Усеченная пирамида, полученная путем усечения пирамиды или конуса;
• Четырехугольные шестигранные призматоиды :
  1. Параллелепипеды – шесть граней параллелограмма
  2. Ромбоэдры – шесть ромбовидных граней
  3. Тригональные трапецоэдры – шесть конгруэнтных ромбовидных граней
  4. Кубоиды – шесть прямоугольных граней
  5. Четырехугольная усеченная квадратная пирамида – вершина – усеченная квадратная пирамида
  6. Куб – шесть квадратных граней

Более высокие измерения

Тетраэдрическо-кубооктаэдрический купол.

В общем случае многогранник является призматоидальным, если его вершины находятся в двух гиперплоскостях . Например, в четырех измерениях два многогранника можно разместить в двух параллельных 3-мерных пространствах и соединить их сторонами многогранников.

Ссылки

1. Керн, Уильям Ф.; Блэнд, Джеймс Р. (1938). Solid Messuration с доказательствами. стр. 75.
2. Альсина, Клауди; Нельсен, Роджер Б. (2015). Математическая космическая одиссея: стереометрия в 21 веке. Математическая ассоциация Америки . стр. 85. ISBN 9780883853580.
3. Meserve, BE; Pingry, RE (1952). «Некоторые заметки о призмоидальной формуле». Учитель математики . 45 (4): 257–263. JSTOR  27954012.

Внешние ссылки

• Вайсштейн, Эрик В. «Призматоид». Математический мир .