Приоритетная очередь

Абстрактный тип данных в информатике

В информатике приоритетная очередь — это абстрактный тип данных, аналогичный обычной очереди или стековому абстрактному типу данных. Каждый элемент в приоритетной очереди имеет связанный с ним приоритет. В приоритетной очереди элементы с высоким приоритетом обслуживаются раньше элементов с низким приоритетом. В некоторых реализациях, если два элемента имеют одинаковый приоритет, они обслуживаются в том же порядке, в котором они были поставлены в очередь. В других реализациях порядок элементов с одинаковым приоритетом не определен.

Хотя приоритетные очереди часто реализуются с использованием куч , они концептуально отличаются от куч. Приоритетная очередь — это абстрактный тип данных, такой как список или карта ; так же, как список может быть реализован с помощью связанного списка или массива , приоритетная очередь может быть реализована с помощью кучи или другого метода, такого как упорядоченный массив.

Операции

Приоритетная очередь должна как минимум поддерживать следующие операции:

• is_empty : проверяет, нет ли в очереди элементов.
• insert_with_priority : добавить элемент в очередь с соответствующим приоритетом.
• pull_highest_priority_element : удалить элемент из очереди, имеющий наивысший приоритет , и вернуть его.

  Это также известно как « pop_element(Off) », « get_maximum_element » или « get_front(most)_element ».

  Некоторые соглашения меняют порядок приоритетов на обратный, считая более низкие значения более приоритетными, поэтому это также может быть известно как « get_minimum_element », а в литературе часто упоминается как « get-min ».

  Вместо этого это можно указать как отдельные функции « peek_at_highest_priority_element » и « delete_element », которые можно объединить для получения « pull_highest_priority_element ».

Кроме того, peek (в этом контексте часто называемый find-max или find-min ), который возвращает элемент с наивысшим приоритетом, но не изменяет очередь, очень часто реализуется и почти всегда выполняется за время O (1) . Эта операция и ее производительность O (1) имеют решающее значение для многих приложений приоритетных очередей.

Более продвинутые реализации могут поддерживать более сложные операции, такие как pull_lowest_priority_element , проверку первых нескольких элементов с наивысшим или наименьшим приоритетом, очистку очереди, очистку подмножеств очереди, выполнение пакетной вставки, объединение двух или более очередей в одну, увеличение приоритета любого элемента и т. д.

Стеки и очереди могут быть реализованы как особые виды очередей приоритетов, где приоритет определяется порядком, в котором вставляются элементы. В стеке приоритет каждого вставленного элемента монотонно увеличивается; таким образом, последний вставленный элемент всегда извлекается первым. В очереди приоритет каждого вставленного элемента монотонно уменьшается; таким образом, первый вставленный элемент всегда извлекается первым.

Выполнение

Наивные реализации

Существует множество простых, обычно неэффективных способов реализации приоритетной очереди. Они предоставляют аналогию, помогающую понять, что такое приоритетная очередь.

Например, можно хранить все элементы в несортированном списке ( время вставки O (1)). Всякий раз, когда запрашивается элемент с наивысшим приоритетом, выполняется поиск по всем элементам для элемента с наивысшим приоритетом. ( время извлечения O ( n )),

вставить (узел) { список.добавить(узел)}

тянуть () { наивысший = список.получить_первый_элемент() foreach узел в списке { если наивысший.приоритет < приоритет.узла { наивысший = узел } } список.удалить(самый высокий) возвращение наивысшего}

В другом случае можно сохранить все элементы в списке, отсортированном по приоритету ( время сортировки вставкой O (n)), и всякий раз, когда запрашивается элемент с наивысшим приоритетом, может быть возвращен первый элемент в списке ( время извлечения O (1)) .

вставить (узел) { foreach (индекс, элемент) в списке { если узел.приоритет < элемент.приоритет { список.вставить_в_индекс(узел,индекс) перерыв } }}

тянуть () { самый высокий = список.получить_по_индексу(список.длина-1) список.удалить(самый высокий) возвращение наивысшего}

Обычная реализация

Для повышения производительности очереди с приоритетами обычно основаны на куче , что дает производительность O (log n ) для вставок и удалений и O ( n ) для первоначального построения кучи из набора из n элементов. Варианты базовой структуры данных кучи, такие как парные кучи или кучи Фибоначчи, могут обеспечить лучшие границы для некоторых операций. ^[1]

В качестве альтернативы, когда используется самобалансирующееся двоичное дерево поиска , вставка и удаление также занимают O (log n ) времени, хотя построение деревьев из существующих последовательностей элементов занимает O ( n log n ) времени; это типично, когда у вас уже может быть доступ к этим структурам данных, например, с помощью сторонних или стандартных библиотек. С точки зрения сложности пространства использование самобалансирующегося двоичного дерева поиска со связанным списком требует больше памяти, поскольку оно требует хранения дополнительных ссылок на другие узлы.

С точки зрения вычислительной сложности приоритетные очереди соответствуют алгоритмам сортировки. Раздел об эквивалентности приоритетных очередей и алгоритмов сортировки ниже описывает, как эффективные алгоритмы сортировки могут создавать эффективные приоритетные очереди.

Специализированные кучи

Существует несколько специализированных структур данных кучи , которые либо предоставляют дополнительные операции, либо превосходят реализации на основе кучи для определенных типов ключей, в частности, целочисленных ключей. Предположим, что набор возможных ключей — это {1, 2, ..., C}.

• Когда нужны только insert , find-min и extract-min и в случае целочисленных приоритетов очередь bucket может быть построена как массив C связанных списков плюс указатель top , изначально C . Вставка элемента с ключом k добавляет элемент в k -й список и обновляет top ← min(top, k ) , оба за постоянное время. Extract-min удаляет и возвращает один элемент из списка с индексом top , затем увеличивает top при необходимости, пока он снова не укажет на непустой список; это занимает O ( C ) времени в худшем случае. Эти очереди полезны для сортировки вершин графа по их степени. ^{[2] : 374}
• Дерево ван Эмде Боаса поддерживает операции минимума , максимума , вставки , удаления , поиска , извлечения минимума , извлечения максимума , предшествующего и последующего элементов за время O (log log C ), но имеет стоимость пространства для небольших очередей около O (2 ^{m /2} ), где m — количество бит в значении приоритета. ^[3] Пространство можно значительно уменьшить с помощью хеширования.
• Дерево Fusion Фредмана и Вилларда реализует минимальную операцию за время O (1) и операции insert и extract-min за время. Однако автор утверждает, что «наши алгоритмы имеют только теоретический интерес; постоянные факторы, участвующие во времени выполнения, исключают практическую ценность». [ ^4] ${\displaystyle O(\log n/\log \log C)}$

Для приложений, которые выполняют много операций " peek " для каждой операции "extract-min", временная сложность для действий peek может быть снижена до O (1) во всех реализациях дерева и кучи путем кэширования элемента с наивысшим приоритетом после каждой вставки и удаления. Для вставки это добавляет максимум постоянную стоимость, поскольку вновь вставленный элемент сравнивается только с ранее кэшированным минимальным элементом. Для удаления это добавляет максимум дополнительную стоимость "peek", которая обычно дешевле стоимости удаления, поэтому общая временная сложность не сильно влияет.

Монотонные очереди с приоритетами — это специализированные очереди, оптимизированные для случая, когда ни один элемент не вставляется с более низким приоритетом (в случае min-heap), чем любой ранее извлеченный элемент. Это ограничение удовлетворяется несколькими практическими применениями очередей с приоритетами.

Сводка времени работы

Вот временные сложности ^[5] различных структур данных кучи. Сокращение am. указывает на то, что данная сложность амортизирована, в противном случае это сложность наихудшего случая. Для значения " O ( f )" и " Θ ( f )" см . нотацию Big O. Имена операций предполагают минимальную кучу.

1. make-heap — это операция построения кучи из последовательности из n неотсортированных элементов. Она может быть выполнена за время Θ ( n ), когда meld выполняется за время O (log  n ) (где обе сложности могут быть амортизированы). ^{[6] [7]} Другой алгоритм достигает Θ ( n ) для двоичных куч. ^[8]
2. Для постоянных куч (не поддерживающих reduce-key ) общее преобразование снижает стоимость meld до стоимости insert , в то время как новая стоимость delete-min является суммой старых стоимостей delete-min и meld . ^[11] Здесь это заставляет meld работать за Θ (1) время (амортизированное, если стоимость insert равна ), в то время как delete-min по-прежнему работает за O (log  n ). Применительно к перекошенным биномиальным кучам это дает очереди Бродала-Окасаки, постоянные кучи с оптимальной сложностью в худшем случае. ^[10]
3. Нижняя граница ^[14] верхняя граница ^[15] ${\displaystyle \Omega (\log \log n),}$ ${\displaystyle O(2^{2{\sqrt {\log \log n}}}).}$
4. Очереди Бродала и строгие кучи Фибоначчи достигают оптимальных сложностей в худшем случае для куч. Они были впервые описаны как императивные структуры данных. Очередь Бродала-Окасаки — это постоянная структура данных, достигающая того же оптимума, за исключением того, что ключ уменьшения не поддерживается.

Эквивалентность приоритетных очередей и алгоритмов сортировки

Использование приоритетной очереди для сортировки

Семантика приоритетных очередей естественным образом предполагает метод сортировки: вставьте все элементы, которые должны быть отсортированы, в приоритетную очередь и последовательно удалите их; они выйдут в отсортированном порядке. Это на самом деле процедура, используемая несколькими алгоритмами сортировки , как только слой абстракции, предоставляемый приоритетной очередью, удален. Этот метод сортировки эквивалентен следующим алгоритмам сортировки:

Использование алгоритма сортировки для создания приоритетной очереди

Алгоритм сортировки также может быть использован для реализации очереди приоритетов. В частности, Торуп говорит: ^[21]

Мы представляем общее детерминированное линейное сокращение пространства от очередей с приоритетами до сортировки, подразумевающее, что если мы можем сортировать до n ключей за время S ( n ) на ключ, то существует очередь с приоритетами, поддерживающая удаление и вставку за время O ( S ( n )) и поиск минимума за постоянное время.

То есть, если есть алгоритм сортировки, который может сортировать за O ( S ) времени на ключ, где S является некоторой функцией от n и размера слова , ^[22] то можно использовать данную процедуру для создания очереди с приоритетами, где извлечение элемента с наивысшим приоритетом занимает O (1) времени, а вставка новых элементов (и удаление элементов) занимает O ( S ) времени. Например, если есть алгоритм сортировки O ( n  log  n ), можно создать очередь с приоритетами с O (1) извлечением и O ( log  n ) вставкой.

Библиотеки

Приоритетную очередь часто считают « контейнерной структурой данных ».

Стандартная библиотека шаблонов (STL) и стандарт C++ 1998 определяют std::priority_queue как один из шаблонов классов адаптеров контейнеров STL . Однако он не определяет, как должны обслуживаться два элемента с одинаковым приоритетом, и, действительно, общие реализации не будут возвращать их в соответствии с их порядком в очереди. Он реализует очередь с максимальным приоритетом и имеет три параметра: объект сравнения для сортировки, такой как объект функции (по умолчанию less<T>, если не указано), базовый контейнер для хранения структур данных (по умолчанию std::vector<T>) и два итератора в начало и конец последовательности. В отличие от реальных контейнеров STL, он не допускает итерации своих элементов (он строго придерживается своего определения абстрактного типа данных). STL также имеет служебные функции для управления другим контейнером с произвольным доступом как двоичной max-heap. Библиотеки Boost также имеют реализацию в библиотечной куче.

Модуль Python heapq реализует двоичную минимальную кучу поверх списка.

Библиотека JavaPriorityQueue содержит класс, который реализует очередь с минимальным приоритетом в виде двоичной кучи.

Библиотека .NET содержит класс PriorityQueue, который реализует четвертичную минимальную кучу на основе массива.

Библиотека Scala содержит класс PriorityQueue, который реализует очередь с максимальным приоритетом.

Библиотека Go содержит модуль контейнера/кучи, который реализует минимальную кучу поверх любой совместимой структуры данных.

Расширение стандартной библиотеки PHP содержит класс SplPriorityQueue.

Фреймворк Core Foundation компании Apple содержит структуру CFBinaryHeap, которая реализует минимальную кучу.

Приложения

Управление пропускной способностью

Приоритетная очередь может использоваться для управления ограниченными ресурсами, такими как полоса пропускания на линии передачи от сетевого маршрутизатора . В случае возникновения очереди исходящего трафика из-за недостаточной пропускной способности все остальные очереди могут быть остановлены для отправки трафика из очереди с наивысшим приоритетом по прибытии. Это гарантирует, что приоритетный трафик (такой как трафик в реальном времени, например, поток RTP VoIP- соединения) будет пересылаться с наименьшей задержкой и наименьшей вероятностью отклонения из-за достижения очередью максимальной емкости. Весь остальной трафик может обрабатываться, когда очередь с наивысшим приоритетом пуста. Другой используемый подход заключается в отправке непропорционально большего количества трафика из очередей с более высоким приоритетом.

Многие современные протоколы для локальных сетей также включают концепцию приоритетных очередей на подуровне управления доступом к среде (MAC), чтобы гарантировать, что высокоприоритетные приложения (такие как VoIP или IPTV ) испытывают меньшую задержку, чем другие приложения, которые могут обслуживаться с наилучшими усилиями . Примерами являются IEEE 802.11e (поправка к IEEE 802.11 , которая обеспечивает качество обслуживания ) и ITU-T G.hn (стандарт для высокоскоростной локальной сети, использующей существующую домашнюю проводку ( линии электропередач , телефонные линии и коаксиальные кабели ).

Обычно ограничение (policer) устанавливается для ограничения полосы пропускания, которую может занять трафик из очереди с наивысшим приоритетом, чтобы не допустить, чтобы пакеты с высоким приоритетом перекрывали весь остальной трафик. Этот предел обычно никогда не достигается из-за высокоуровневых контрольных экземпляров, таких как Cisco Callmanager, которые можно запрограммировать на блокировку вызовов, которые могут превысить запрограммированный предел полосы пропускания.

Дискретное событийное моделирование

Другое применение приоритетной очереди — управление событиями в дискретном моделировании событий . События добавляются в очередь, а время их моделирования используется в качестве приоритета. Выполнение моделирования происходит путем многократного вытягивания вершины очереди и выполнения события на ней.

См. также : Планирование (вычисления) , теория очередей

Алгоритм Дейкстры

Если граф хранится в виде списка смежности или матрицы, то для эффективного извлечения минимума при реализации алгоритма Дейкстры можно использовать приоритетную очередь , хотя также необходима возможность эффективно изменять приоритет конкретной вершины в приоритетной очереди.

Если вместо этого граф хранится как объекты узлов, а пары приоритет-узел вставляются в кучу, изменение приоритета конкретной вершины не требуется, если отслеживаются посещенные узлы. После посещения узла, если он снова появляется в куче (имея ранее связанный с ним более низкий номер приоритета), он выталкивается и игнорируется.

Кодирование Хаффмана

Кодирование Хаффмана требует многократного получения двух деревьев с самой низкой частотой. Приоритетная очередь — один из методов сделать это .

Алгоритмы поиска по принципу «лучшее-первое»

Алгоритмы поиска «лучший первый» , такие как алгоритм поиска A* , находят кратчайший путь между двумя вершинами или узлами взвешенного графа , пробуя сначала наиболее перспективные маршруты. Очередь приоритетов (также известная как fringe ) используется для отслеживания неисследованных маршрутов; тот, для которого оценка (нижняя граница в случае A*) общей длины пути наименьшая, получает наивысший приоритет. Если ограничения памяти делают поиск «лучший первый» непрактичным, вместо него можно использовать варианты, такие как алгоритм SMA* , с двухсторонней очередью приоритетов , чтобы разрешить удаление элементов с низким приоритетом.

Алгоритм триангуляции ROAM

Алгоритм Real-time Optimally Adapting Meshes ( ROAM ) вычисляет динамически изменяющуюся триангуляцию рельефа. Он работает путем разделения треугольников, где требуется больше деталей, и их объединения, где требуется меньше деталей. Алгоритм назначает каждому треугольнику на рельефе приоритет, обычно связанный с уменьшением ошибки, если бы этот треугольник был разделен. Алгоритм использует две очереди приоритетов, одну для треугольников, которые можно разделить, и другую для треугольников, которые можно объединить. На каждом шаге треугольник из очереди разделения с наивысшим приоритетом разделяется, или треугольник из очереди слияния с наименьшим приоритетом объединяется со своими соседями.

Алгоритм Прима для минимального остовного дерева

Используя очередь приоритета минимальной кучи в алгоритме Прима для поиска минимального остовного дерева связного и неориентированного графа , можно добиться хорошего времени выполнения. Эта очередь приоритета минимальной кучи использует структуру данных минимальной кучи, которая поддерживает такие операции, как вставка , минимум , извлечение минимума , уменьшение ключа . ^[23] В этой реализации вес ребер используется для определения приоритета вершин . Чем меньше вес, тем выше приоритет, а чем больше вес, тем ниже приоритет. ^[24]

Параллельная приоритетная очередь

Распараллеливание может использоваться для ускорения приоритетных очередей, но требует некоторых изменений в интерфейсе приоритетной очереди. Причина таких изменений в том, что последовательное обновление обычно имеет только или стоимость, и нет практического выигрыша от распараллеливания такой операции. Одним из возможных изменений является разрешение одновременного доступа нескольких процессоров к одной и той же приоритетной очереди. Вторым возможным изменением является разрешение пакетных операций, которые работают с элементами, а не только с одним элементом. Например, extractMin удалит первые элементы с наивысшим приоритетом. ${\textstyle O(1)}$ ${\textstyle O(\log n)}$ ${\textstyle k}$ ${\textstyle k}$

Одновременный параллельный доступ

Если приоритетная очередь допускает параллельный доступ, несколько процессов могут выполнять операции одновременно в этой приоритетной очереди. Однако это поднимает две проблемы. Во-первых, определение семантики отдельных операций больше не очевидно. Например, если два процесса хотят извлечь элемент с наивысшим приоритетом, должны ли они получить один и тот же элемент или разные? Это ограничивает параллелизм на уровне программы, использующей приоритетную очередь. Кроме того, поскольку несколько процессов имеют доступ к одному и тому же элементу, это приводит к конкуренции.

Узел 3 вставляется и устанавливает указатель узла 2 на узел 3. Сразу после этого узел 2 удаляется, а указатель узла 1 устанавливается на узел 4. Теперь узел 3 больше недоступен.

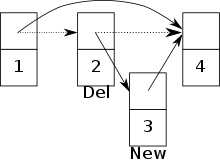
Параллельный доступ к приоритетной очереди может быть реализован на модели PRAM Concurrent Read, Concurrent Write (CRCW). В дальнейшем приоритетная очередь реализована как список пропусков . ^{[25] [26]} Кроме того, примитив атомарной синхронизации CAS используется для того, чтобы сделать список пропусков неблокируемым . Узлы списка пропусков состоят из уникального ключа, приоритета, массива указателей для каждого уровня на следующие узлы и метки удаления . Метка удаления отмечает , что узел собирается быть удаленным процессом. Это гарантирует, что другие процессы смогут соответствующим образом отреагировать на удаление.

• insert(e) : Сначала создается новый узел с ключом и приоритетом. Кроме того, узлу назначается количество уровней, которое определяет размер массива указателей. Затем выполняется поиск для нахождения правильной позиции, куда следует вставить новый узел. Поиск начинается с первого узла и с самого высокого уровня. Затем список пропусков просматривается до самого низкого уровня, пока не будет найдена правильная позиция. Во время поиска для каждого уровня последний пройденный узел будет сохранен как родительский узел для нового узла на этом уровне. Кроме того, узел, на который указывает указатель на этом уровне родительского узла, будет сохранен как последующий узел нового узла на этом уровне. После этого для каждого уровня нового узла указатели родительского узла будут установлены на новый узел. Наконец, указатели для каждого уровня нового узла будут установлены на соответствующие последующие узлы.
• extract-min : Сначала список пропусков просматривается до тех пор, пока не будет достигнут узел, метка удаления которого не установлена. Затем эта метка удаления устанавливается в значение true для этого узла. Наконец, обновляются указатели родительских узлов удаленного узла.

Если разрешен одновременный доступ к приоритетной очереди, между двумя процессами могут возникнуть конфликты. Например, конфликт возникает, если один процесс пытается вставить новый узел, но в то же время другой процесс собирается удалить предшественника этого узла. ^[25] Существует риск того, что новый узел будет добавлен в список пропуска, но он больше не будет доступен. ( См. изображение )

К-элементные операции

В этой настройке операции с приоритетной очередью обобщаются на пакет элементов. Например, k_extract-min удаляет наименьшие элементы приоритетной очереди и возвращает их. ${\textstyle k}$ ${\textstyle k}$

В условиях разделяемой памяти параллельная приоритетная очередь может быть легко реализована с использованием параллельных двоичных деревьев поиска и алгоритмов дерева на основе объединения . В частности, k_extract-min соответствует разделению на двоичном дереве поиска, которое имеет стоимость и дает дерево, содержащее наименьшие элементы. k_insert может быть применено путем объединения исходной приоритетной очереди и пакета вставок. Если пакет уже отсортирован по ключу, k_insert имеет стоимость. В противном случае нам нужно сначала отсортировать пакет, поэтому стоимость будет . Другие операции для приоритетной очереди могут быть применены аналогичным образом. Например, k_decrease-key может быть выполнено путем применения сначала разности , а затем объединения , которое сначала удаляет элементы, а затем вставляет их обратно с обновленными ключами. Все эти операции высокопараллельны, и теоретическую и практическую эффективность можно найти в соответствующих исследовательских работах. ^{[27] [28]} ${\textstyle O(\log n)}$ ${\textstyle k}$ ${\textstyle O(k\log(1+{\frac {n}{k}}))}$ ${\textstyle O(k\log(1+{\frac {n}{k}})+k\log k)=O(k\log n)}$

Остальная часть этого раздела посвящена алгоритму на основе очередей в распределенной памяти. Мы предполагаем, что каждый процессор имеет свою собственную локальную память и локальную (последовательную) приоритетную очередь. Элементы глобальной (параллельной) приоритетной очереди распределены по всем процессорам.

k_extract-min выполняется в приоритетной очереди с тремя процессорами. Зеленые элементы возвращаются и удаляются из приоритетной очереди.

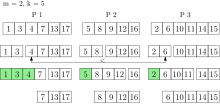
Операция k_insert назначает элементы равномерно случайным образом процессорам, которые вставляют элементы в свои локальные очереди. Обратите внимание, что отдельные элементы все еще могут быть вставлены в очередь. При использовании этой стратегии глобальные наименьшие элементы находятся в объединении локальных наименьших элементов каждого процессора с высокой вероятностью. Таким образом, каждый процессор удерживает репрезентативную часть глобальной приоритетной очереди.

Это свойство используется при выполнении k_extract-min , поскольку наименьшие элементы каждой локальной очереди удаляются и собираются в набор результатов. Элементы в наборе результатов по-прежнему связаны с их исходным процессором. Количество элементов, удаляемых из каждой локальной очереди, зависит от и количества процессоров . ^[29] С помощью параллельного выбора определяются наименьшие элементы набора результатов. С высокой вероятностью это глобальные наименьшие элементы. Если нет, элементы снова удаляются из каждой локальной очереди и помещаются в набор результатов. Это делается до тех пор, пока в наборе результатов не окажутся глобальные наименьшие элементы. Теперь эти элементы можно вернуть. Все остальные элементы набора результатов вставляются обратно в свои локальные очереди. Ожидается время выполнения k_extract-min , где и — размер приоритетной очереди. ^[29] ${\textstyle m}$ ${\textstyle m}$ ${\textstyle k}$ ${\textstyle p}$ ${\textstyle k}$ ${\textstyle k}$ ${\textstyle m}$ ${\textstyle k}$ ${\textstyle k}$ ${\textstyle O({\frac {k}{p}}\log(n))}$ ${\textstyle k=\Omega (p\cdot \log(p))}$ ${\textstyle n}$

Приоритетную очередь можно дополнительно улучшить, не перемещая оставшиеся элементы набора результатов напрямую обратно в локальные очереди после операции k_extract-min . Это экономит перемещение элементов туда и обратно все время между набором результатов и локальными очередями.

Удаляя несколько элементов одновременно, можно достичь значительного ускорения. Но не все алгоритмы могут использовать этот тип очереди с приоритетами. Например, алгоритм Дейкстры не может работать на нескольких узлах одновременно. Алгоритм берет узел с наименьшим расстоянием от очереди с приоритетами и вычисляет новые расстояния для всех его соседних узлов. Если бы вы удалили узлы, работа с одним узлом могла бы изменить расстояние до другого узла . Таким образом, использование операций с k-элементами разрушает свойство установки меток алгоритма Дейкстры. ${\textstyle k}$ ${\textstyle k}$

Смотрите также

• Пакетная очередь
• Очередь команд
• Планировщик заданий

Ссылки

1. Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Стайн, Клиффорд (2001) [1990]. "Глава 20: Кучи Фибоначчи". Введение в алгоритмы (2-е изд.). MIT Press и McGraw-Hill. стр. 476–497. ISBN 0-262-03293-7.Третье издание, стр. 518.
2. Скиена, Стивен (2010). Руководство по разработке алгоритмов (2-е изд.). Springer Science+Business Media . ISBN 978-1-849-96720-4.
3. П. ван Эмде Боас. Сохранение порядка в лесу за время, меньшее, чем логарифмическое. В трудах 16-го ежегодного симпозиума по основам компьютерной науки , страницы 75-84. IEEE Computer Society, 1975.
4. Майкл Л. Фредман и Дэн Э. Уиллард. Преодоление теоретической границы информации с помощью деревьев слияния. Журнал компьютерных и системных наук , 48(3):533-551, 1994
5. Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л. (1990). Введение в алгоритмы (1-е изд.). MIT Press и McGraw-Hill. ISBN 0-262-03141-8.
6. Sleator, Daniel Dominic ; Tarjan, Robert Endre (февраль 1986 г.). «Саморегулирующиеся кучи». SIAM Journal on Computing . 15 (1): 52–69. CiteSeerX 10.1.1.93.6678 . doi :10.1137/0215004. ISSN  0097-5397. 
7. Tarjan, Robert (1983). "3.3. Левые кучи". Структуры данных и сетевые алгоритмы . стр. 38–42. doi :10.1137/1.9781611970265. ISBN 978-0-89871-187-5.
8. Хейворд, Райан; МакДиармид, Колин (1991). "Анализ среднего случая построения кучи путем повторной вставки" (PDF) . J. Algorithms . 12 : 126–153. CiteSeerX 10.1.1.353.7888 . doi :10.1016/0196-6774(91)90027-v. Архивировано из оригинала (PDF) 2016-02-05 . Получено 2016-01-28 . 
9. "Биномиальная куча | Brilliant Math & Science Wiki". brilliant.org . Получено 2019-09-30 .
10. Brodal, Gerth Stølting; Okasaki, Chris (ноябрь 1996 г.), «Оптимальные чисто функциональные очереди с приоритетами», Journal of Functional Programming , 6 (6): 839–857, doi : 10.1017/s095679680000201x
11. Окасаки, Крис (1998). "10.2. Структурная абстракция". Чисто функциональные структуры данных (1-е изд.). С. 158–162. ISBN 9780521631242.
12. Такаока, Тадао (1999), Теория 2–3 куч (PDF) , стр. 12
13. Яконо, Джон (2000), «Улучшенные верхние границы для парных куч», Труды 7-го Скандинавского семинара по теории алгоритмов (PDF) , Lecture Notes in Computer Science, т. 1851, Springer-Verlag, стр. 63–77, arXiv : 1110.4428 , CiteSeerX 10.1.1.748.7812 , doi : 10.1007/3-540-44985-X_5, ISBN  3-540-67690-2
14. Фредман, Майкл Лоуренс (июль 1999 г.). «Об эффективности парных куч и связанных с ними структур данных» (PDF) . Журнал Ассоциации вычислительной техники . 46 (4): 473–501. doi :10.1145/320211.320214.
15. Pettie, Seth (2005). Towards a Final Analysis of Pairing Heaps (PDF) . Труды FOCS '05 46-го ежегодного симпозиума IEEE по основам компьютерной науки. стр. 174–183. CiteSeerX 10.1.1.549.471 . doi :10.1109/SFCS.2005.75. ISBN  0-7695-2468-0.
16. Хёплер, Бернхард; Сен, Сиддхартха; Тарьян, Роберт Э. (ноябрь 2011 г.). «Кучи ранговых пар» (PDF) . СИАМ Дж. Компьютерные технологии . 40 (6): 1463–1485. дои : 10.1137/100785351.
17. Фредман, Майкл Лоуренс ; Тарьян, Роберт Э. (июль 1987 г.). «Кучи Фибоначчи и их использование в улучшенных алгоритмах сетевой оптимизации» (PDF) . Журнал Ассоциации вычислительной техники . 34 (3): 596–615. CiteSeerX 10.1.1.309.8927 . doi :10.1145/28869.28874. 
18. Бродал, Герт Столтинг ; Лагогианнис, Джордж; Тарьян, Роберт Э. (2012). Строгие кучи Фибоначчи (PDF) . Труды 44-го симпозиума по теории вычислений - STOC '12. стр. 1177–1184. CiteSeerX 10.1.1.233.1740 . doi :10.1145/2213977.2214082. ISBN  978-1-4503-1245-5.
19. Бродал, Герт С. (1996), «Эффективные очереди с приоритетами в наихудшем случае» (PDF) , Труды 7-го ежегодного симпозиума ACM-SIAM по дискретным алгоритмам , стр. 52–58
20. Гудрич, Майкл Т .; Тамассиа, Роберто (2004). "7.3.6. Построение кучи снизу вверх". Структуры данных и алгоритмы в Java (3-е изд.). С. 338–341. ISBN 0-471-46983-1.
21. Торуп, Миккель (2007). «Эквивалентность приоритетных очередей и сортировки». Журнал ACM . 54 (6): 28. doi :10.1145/1314690.1314692. S2CID  11494634.
22. "Архивная копия" (PDF) . Архивировано (PDF) из оригинала 2011-07-20 . Получено 2011-02-10 .{{cite web}}: CS1 maint: архивная копия как заголовок ( ссылка )
23. Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2009) [1990]. Введение в алгоритмы (3-е изд.). MIT Press и McGraw-Hill. п. 634. ИСБН 0-262-03384-4.«Чтобы эффективно реализовать алгоритм Прима, нам нужен быстрый способ выбора нового ребра для добавления в дерево, образованное ребрами в A».
24. "Алгоритм Прима". Geek for Geeks. 18 ноября 2012 г. Архивировано из оригинала 9 сентября 2014 г. Получено 12 сентября 2014 г.
25. Sundell, Håkan; Tsigas, Philippas (2005). «Быстрые и неблокируемые параллельные приоритетные очереди для многопоточных систем». Журнал параллельных и распределенных вычислений . 65 (5): 609–627. CiteSeerX 10.1.1.67.1310 . doi :10.1109/IPDPS.2003.1213189. S2CID  20995116. 
26. Линден, Йонссон (2013), «Конкурентная приоритетная очередь на основе списка пропусков с минимальным конфликтом памяти», Технический отчет 2018-003 (на немецком языке)
27. Blelloch, Guy E.; Ferizovic, Daniel; Sun, Yihan (2016), «Just Join for Parallel Ordered Sets», Симпозиум по параллельным алгоритмам и архитектурам, Труды 28-го симпозиума ACM. Параллельные алгоритмы и архитектуры (SPAA 2016) , ACM, стр. 253–264, arXiv : 1602.02120 , doi : 10.1145/2935764.2935768, ISBN 978-1-4503-4210-0, S2CID  2897793
28. Blelloch, Guy E.; Ferizovic, Daniel; Sun, Yihan (2018), «PAM: параллельные расширенные карты», Труды 23-го симпозиума ACM SIGPLAN по принципам и практике параллельного программирования , ACM, стр. 290–304
29. Сандерс, Питер; Мельхорн, Курт; Дицфельбингер, Мартин; Дементьев, Роман (2019). Последовательные и параллельные алгоритмы и структуры данных — базовый набор инструментов . Springer International Publishing. стр. 226–229. doi :10.1007/978-3-030-25209-0. ISBN 978-3-030-25208-3. S2CID  201692657.

Дальнейшее чтение

• Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2001) [1990]. "Раздел 6.5: Приоритетные очереди". Введение в алгоритмы (2-е изд.). MIT Press и McGraw-Hill. стр. 138–142. ISBN 0-262-03293-7.

Внешние ссылки

• Справочник C++ для std::priority_queue
• Описания Ли Киллоу
• libpqueue — это универсальная реализация приоритетной очереди (кучи) (на языке C), используемая проектом Apache HTTP Server.
• Обзор известных структур приоритетных очередей Стефана Ксеноса
• Калифорнийский университет в Беркли — Информатика 61B — Лекция 24: Приоритетные очереди (видео) — введение в приоритетные очереди с использованием двоичной кучи