Формальная грамматика

Пример формальной грамматики с проанализированным предложением. Формальные грамматики состоят из набора нетерминальных символов, терминальных символов, правил производства и назначенного начального символа.

Структура формального языка

Формальная грамматика описывает, какие строки из алфавита формального языка являются допустимыми в соответствии с синтаксисом языка . Грамматика не описывает значение строк или то, что можно сделать с ними в любом контексте — только их форму. Формальная грамматика определяется как набор правил производства для таких строк в формальном языке.

Формальная теория языка, дисциплина, изучающая формальные грамматики и языки, является разделом прикладной математики . Её приложения встречаются в теоретической информатике , теоретической лингвистике , формальной семантике , математической логике и других областях.

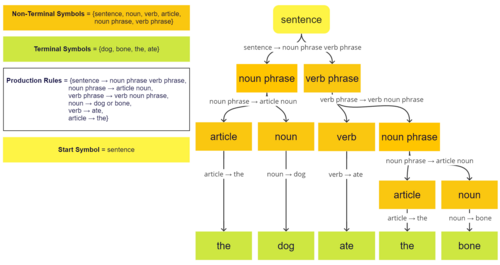
Формальная грамматика — это набор правил для переписывания строк вместе с «начальным символом», с которого начинается переписывание. Поэтому грамматику обычно считают генератором языка. Однако иногда ее также можно использовать в качестве основы для « распознавателя » — функции в вычислениях, которая определяет, принадлежит ли данная строка языку или является грамматически неправильной. Для описания таких распознавателей формальная теория языка использует отдельные формализмы, известные как теория автоматов . Одним из интересных результатов теории автоматов является то, что невозможно разработать распознаватель для определенных формальных языков. ^[1] Синтаксический анализ — это процесс распознавания высказывания (строки в естественных языках) путем разбиения его на набор символов и анализа каждого из них в соответствии с грамматикой языка. Большинство языков имеют значения своих высказываний, структурированные в соответствии с их синтаксисом — практика, известная как композиционная семантика . В результате первым шагом к описанию смысла высказывания в языке является его разбиение на части и рассмотрение его проанализированной формы (известной как дерево синтаксического анализа в информатике и как его глубокая структура в генеративной грамматике ).

Вводный пример

Грамматика в основном состоит из набора правил производства , правил переписывания для преобразования строк. Каждое правило определяет замену определенной строки (ее левой части ) на другую (ее правую часть ). Правило может быть применено к каждой строке, содержащей ее левую часть, и создает строку, в которой вхождение этой левой части было заменено ее правой частью.

В отличие от полусистемы Туэ , которая полностью определяется этими правилами, грамматика далее различает два вида символов: нетерминальные и терминальные символы ; каждая левая часть должна содержать по крайней мере один нетерминальный символ. Она также различает специальный нетерминальный символ, называемый начальным символом .

Язык, генерируемый грамматикой, определяется как множество всех строк без каких-либо нетерминальных символов, которые могут быть сгенерированы из строки, состоящей из одного начального символа, путем (возможно, повторного) применения ее правил любым возможным способом. Если существуют существенно различные способы генерации одной и той же строки, грамматика называется неоднозначной .

В следующих примерах конечными символами являются a и b , а начальным символом — S.

Пример 1

Предположим, у нас есть следующие правила производства:

1. ${\displaystyle S\rightarrow aSb}$

2. ${\displaystyle S\rightarrow ba}$

затем мы начинаем с S и можем выбрать правило, которое будет к нему применено. Если мы выберем правило 1, то получим строку aSb . Если мы затем снова выберем правило 1, то заменим S на aSb и получим строку aaSbb . Если мы теперь выберем правило 2, то заменим S на ba и получим строку aababb , и все готово. Мы можем записать эту серию выборов более кратко, используя символы: . ${\displaystyle S\Rightarrow aSb\Rightarrow aaSbb\Rightarrow aababb}$

Язык грамматики — бесконечное множество , где повторяется раз (и, в частности, представляет собой количество раз, когда было применено правило производства 1). Эта грамматика является контекстно-свободной (только отдельные нетерминалы появляются в качестве левых частей) и однозначной. ${\displaystyle \{a^{n}bab^{n}\mid n\geq 0\}=\{ba,abab,aababb,aaababbb,\dotsc \}}$ ${\displaystyle a^{k}}$ ${\displaystyle a}$ ${\displaystyle k}$ ${\displaystyle n}$

Примеры 2 и 3

Предположим, что правила таковы:

1. ${\displaystyle S\rightarrow a}$

2. ${\displaystyle S\rightarrow SS}$

3. ${\displaystyle aSa\rightarrow b}$

Эта грамматика не является контекстно-свободной из-за правила 3 ​​и неоднозначна из-за множественных способов использования правила 2 для генерации последовательностей s. ${\displaystyle S}$

Однако язык, который он генерирует, — это просто набор всех непустых строк, состоящих из s и/или s. Это легко увидеть: чтобы сгенерировать a из an , дважды используйте правило 2 для генерации , затем дважды правило 1 и один раз правило 3 для генерации . Это означает, что мы можем генерировать произвольные непустые последовательности s, а затем заменять каждую из них на или по своему усмотрению. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle b}$ ${\displaystyle S}$ ${\displaystyle SSS}$ ${\displaystyle b}$ ${\displaystyle S}$ ${\displaystyle a}$ ${\displaystyle b}$

Этот же язык может быть альтернативно сгенерирован с помощью контекстно-свободной, однозначной грамматики; например, регулярной грамматики с правилами

1. ${\displaystyle S\rightarrow aS}$

2. ${\displaystyle S\rightarrow bS}$

3. ${\displaystyle S\rightarrow a}$

4. ${\displaystyle S\rightarrow b}$

Формальное определение

Синтаксис грамматик

В классической формализации генеративных грамматик, впервые предложенной Ноамом Хомским в 1950-х годах, ^{[2] [3]} грамматика G состоит из следующих компонентов:

• Конечное множество N нетерминальных символов , не пересекающееся со строками, образованными из G.
• Конечное множество терминальных символов , не пересекающееся с N. ${\displaystyle \Sigma }$
• Конечный набор P правил производства , каждое правило имеет вид

${\displaystyle (\Sigma \cup N)^{*}N(\Sigma \cup N)^{*}\rightarrow (\Sigma \cup N)^{*}}$

где — оператор звезды Клини , а обозначает объединение множеств . То есть каждое правило продукции отображает одну строку символов в другую, где первая строка («голова») содержит произвольное количество символов, при условии, что хотя бы один из них является нетерминалом. В случае, если вторая строка («тело») состоит исключительно из пустой строки — т. е. она вообще не содержит символов — она может быть обозначена специальной нотацией (часто , e или ), чтобы избежать путаницы. Такое правило называется правилом стирания . ^[4] ${\displaystyle {*}}$ ${\displaystyle \cup }$ ${\displaystyle \Lambda }$ ${\displaystyle \epsilon }$

• Выдающийся символ , являющийся начальным символом , также называемый символом предложения . ${\displaystyle S\in N}$

Грамматика формально определяется как кортеж . Такая формальная грамматика часто называется в литературе системой переписывания или грамматикой фразовой структуры . ^{[5] [6]} ${\displaystyle (N,\Sigma ,P,S)}$

Некоторые математические конструкции, касающиеся формальных грамматик

Действие грамматики можно определить в терминах отношений на строках:

• Учитывая грамматику , бинарное отношение (произносится как «G выводится за один шаг») на строках определяется следующим образом: ${\displaystyle G=(N,\Sigma ,P,S)}$ ${\displaystyle {\underset {G}{\Rightarrow }}}$ ${\displaystyle (\Sigma \cup N)^{*}}$

  ${\displaystyle x{\underset {G}{\Rightarrow }}y\iff \exists u,v,p,q\in (\Sigma \cup N)^{*}:(x=upv)\wedge (p\rightarrow q\in P)\wedge (y=uqv)}$

• отношение (произносится как G выводится за ноль или более шагов ) определяется как рефлексивное транзитивное замыкание ${\displaystyle {\overset {*}{\underset {G}{\Rightarrow }}}}$ ${\displaystyle {\underset {G}{\Rightarrow }}}$
• асентенциальная форма — это член , который может быть получен за конечное число шагов из начального символа ; то есть сентенциальная форма — это член . Сентенциальная форма, которая не содержит нетерминальных символов (то есть является членом ), называется предложением . ^[7] ${\displaystyle (\Sigma \cup N)^{*}}$ ${\displaystyle S}$ ${\displaystyle \left\{w\in (\Sigma \cup N)^{*}\mid S{\overset {*}{\underset {G}{\Rightarrow }}}w\right\}}$ ${\displaystyle \Sigma ^{*}}$
• язык , обозначаемый как , определяется как набор предложений, построенных . ${\displaystyle G}$ ${\displaystyle {\boldsymbol {L}}(G)}$ ${\displaystyle G}$

Грамматика фактически представляет собой полусистему Туэ , перезаписывающую строки точно таким же образом; единственное отличие состоит в том, что мы выделяем определенные нетерминальные символы, которые должны быть перезаписаны в правилах перезаписи, и интересуемся только перезаписями от обозначенного начального символа до строк без нетерминальных символов. ${\displaystyle G=(N,\Sigma ,P,S)}$ ${\displaystyle (N\cup \Sigma ,P)}$ ${\displaystyle S}$

Пример

В этих примерах формальные языки определяются с использованием нотации конструктора множеств .

Рассмотрим грамматику , где , , — начальный символ, и она состоит из следующих правил продукций: ${\displaystyle G}$ ${\displaystyle N=\left\{S,B\right\}}$ ${\displaystyle \Sigma =\left\{a,b,c\right\}}$ ${\displaystyle S}$ ${\displaystyle P}$

1. ${\displaystyle S\rightarrow aBSc}$

2. ${\displaystyle S\rightarrow abc}$

3. ${\displaystyle Ba\rightarrow aB}$

4. ${\displaystyle Bb\rightarrow bb}$

Эта грамматика определяет язык , где обозначает строку из n последовательных '. Таким образом, язык — это набор строк, которые состоят из 1 или более ', за которыми следует такое же количество ', за которым следует такое же количество '. ${\displaystyle L(G)=\left\{a^{n}b^{n}c^{n}\mid n\geq 1\right\}}$ ${\displaystyle a^{n}}$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$

Вот несколько примеров вывода строк : ${\displaystyle L(G)}$

• ${\displaystyle {\boldsymbol {S}}{\underset {2}{\Rightarrow }}{\boldsymbol {abc}}}$
• ${\displaystyle {\begin{aligned}{\boldsymbol {S}}&{\underset {1}{\Rightarrow }}{\boldsymbol {aBSc}}\\&{\underset {2}{\Rightarrow }}aB{\boldsymbol {abc}}c\\&{\underset {3}{\Rightarrow }}a{\boldsymbol {aB}}bcc\\&{\underset {4}{\Rightarrow }}aa{\boldsymbol {bb}}cc\end{aligned}}}$
• ${\displaystyle {\begin{aligned}{\boldsymbol {S}}&{\underset {1}{\Rightarrow }}{\boldsymbol {aBSc}}{\underset {1}{\Rightarrow }}aB{\boldsymbol {aBSc}}c\\&{\underset {2}{\Rightarrow }}aBaB{\boldsymbol {abc}}cc\\&{\underset {3}{\Rightarrow }}a{\boldsymbol {aB}}Babccc{\underset {3}{\Rightarrow }}aaB{\boldsymbol {aB}}bccc{\underset {3}{\Rightarrow }}aa{\boldsymbol {aB}}Bbccc\\&{\underset {4}{\Rightarrow }}aaaB{\boldsymbol {bb}}ccc{\underset {4}{\Rightarrow }}aaa{\boldsymbol {bb}}bccc\end{aligned}}}$

(В обозначениях: читается как «Строка P порождает строку Q посредством продукции i », а генерируемая часть каждый раз указывается жирным шрифтом.) ${\displaystyle P{\underset {i}{\Rightarrow }}Q}$

Иерархия Хомского

Когда Ноам Хомский впервые формализовал генеративные грамматики в 1956 году, ^[2] он классифицировал их по типам, которые сейчас известны как иерархия Хомского . Разница между этими типами заключается в том, что они имеют все более строгие правила производства и, следовательно, могут выражать меньше формальных языков. Два важных типа — это контекстно-свободные грамматики (тип 2) и регулярные грамматики (тип 3). Языки, которые можно описать с помощью такой грамматики, называются контекстно-свободными языками и регулярными языками соответственно. Хотя они гораздо менее мощные, чем неограниченные грамматики (тип 0), которые фактически могут выражать любой язык, который может быть принят машиной Тьюринга , эти два ограниченных типа грамматик используются чаще всего, поскольку синтаксические анализаторы для них могут быть эффективно реализованы. ^[8] Например, все регулярные языки могут быть распознаны конечным автоматом , и для полезных подмножеств контекстно-свободных грамматик существуют хорошо известные алгоритмы для генерации эффективных LL-анализаторов и LR-анализаторов для распознавания соответствующих языков, которые генерируют эти грамматики.

Контекстно-свободные грамматики

Контекстно -свободная грамматика — это грамматика, в которой левая часть каждого правила производства состоит только из одного нетерминального символа. Это ограничение нетривиально; не все языки могут быть сгенерированы контекстно-свободными грамматиками. Те, которые могут, называются контекстно-свободными языками .

Определенный выше язык не является контекстно-свободным языком, и это можно строго доказать с помощью леммы о накачке для контекстно-свободных языков , но, например, язык (по крайней мере 1, за которым следует такое же количество символов ') является контекстно-свободным, поскольку его можно определить с помощью грамматики с , , начальным символом и следующими правилами вывода: ${\displaystyle L(G)=\left\{a^{n}b^{n}c^{n}\mid n\geq 1\right\}}$ ${\displaystyle \left\{a^{n}b^{n}\mid n\geq 1\right\}}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle G_{2}}$ ${\displaystyle N=\left\{S\right\}}$ ${\displaystyle \Sigma =\left\{a,b\right\}}$ ${\displaystyle S}$

1. ${\displaystyle S\rightarrow aSb}$

2. ${\displaystyle S\rightarrow ab}$

Контекстно-свободный язык может быть распознан со временем ( см. обозначение Big O ) с помощью алгоритма, такого как распознаватель Эрли . То есть, для каждого контекстно-свободного языка можно построить машину, которая принимает строку в качестве входных данных и определяет со временем, является ли строка членом языка, где — длина строки. ^[9] Детерминированные контекстно-свободные языки — это подмножество контекстно-свободных языков, которые могут быть распознаны за линейное время. ^[10] Существуют различные алгоритмы, которые нацелены либо на этот набор языков, либо на некоторое его подмножество. ${\displaystyle O(n^{3})}$ ${\displaystyle O(n^{3})}$ ${\displaystyle n}$

Регулярные грамматики

В обычных грамматиках левая сторона снова представляет собой только один нетерминальный символ, но теперь правая сторона также ограничена. Правая сторона может быть пустой строкой, или одиночным терминальным символом, или одиночным терминальным символом, за которым следует нетерминальный символ, но ничего больше. (Иногда используется более широкое определение: можно разрешить более длинные строки терминалов или одиночные нетерминалы без чего-либо еще, что упрощает обозначение языков , при этом определяя тот же класс языков.)

Определенный выше язык не является регулярным, но язык (по крайней мере 1, за которым следует по крайней мере 1 , где числа могут быть разными) является регулярным, поскольку его можно определить с помощью грамматики с , , начальным символом и следующими правилами производства: ${\displaystyle \left\{a^{n}b^{n}\mid n\geq 1\right\}}$ ${\displaystyle \left\{a^{n}b^{m}\mid m,n\geq 1\right\}}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle G_{3}}$ ${\displaystyle N=\left\{S,A,B\right\}}$ ${\displaystyle \Sigma =\left\{a,b\right\}}$ ${\displaystyle S}$

1. ${\displaystyle S\rightarrow aA}$
2. ${\displaystyle A\rightarrow aA}$
3. ${\displaystyle A\rightarrow bB}$
4. ${\displaystyle B\rightarrow bB}$
5. ${\displaystyle B\rightarrow \epsilon }$

Все языки, сгенерированные регулярной грамматикой, могут быть распознаны со временем конечным автоматом. Хотя на практике регулярные грамматики обычно выражаются с помощью регулярных выражений , некоторые формы регулярных выражений, используемые на практике, не генерируют строго регулярные языки и не показывают линейной производительности распознавания из-за этих отклонений. ${\displaystyle O(n)}$

Другие формы генеративных грамматик

Было разработано много расширений и вариаций оригинальной иерархии формальных грамматик Хомского, как лингвистами, так и специалистами по информатике, обычно либо для того, чтобы увеличить их выразительную силу, либо для того, чтобы сделать их более легкими для анализа или разбора. Некоторые формы разработанных грамматик включают:

• Грамматики, примыкающие к деревьям, увеличивают выразительность обычных генеративных грамматик, позволяя правилам перезаписи работать с деревьями разбора, а не только со строками. ^[11]
• Грамматики аффиксов ^[12] и атрибутивные грамматики ^{[13] [14]} позволяют дополнять правила переписывания семантическими атрибутами и операциями, полезными как для повышения выразительности грамматики, так и для создания практических инструментов языкового перевода.

Рекурсивные грамматики

Рекурсивная грамматика — это грамматика, которая содержит правила производства, которые являются рекурсивными . Например, грамматика для контекстно-свободного языка является леворекурсивной, если существует нетерминальный символ A , который может быть пропущен через правила производства для получения строки с A в качестве самого левого символа. ^[15] Примером рекурсивной грамматики является предложение внутри предложения, разделенное двумя запятыми. ^[16] Все типы грамматик в иерархии Хомского могут быть рекурсивными.

Аналитические грамматики

Хотя существует огромное количество литературы по алгоритмам синтаксического анализа , большинство этих алгоритмов предполагают, что язык, который нужно проанализировать, изначально описан с помощью генеративной формальной грамматики, и что цель состоит в том, чтобы преобразовать эту генеративную грамматику в работающий синтаксический анализатор. Строго говоря, генеративная грамматика никоим образом не соответствует алгоритму, используемому для синтаксического анализа языка, и различные алгоритмы имеют различные ограничения на форму правил производства, которые считаются правильно сформированными.

Альтернативный подход заключается в формализации языка в терминах аналитической грамматики в первую очередь, что более непосредственно соответствует структуре и семантике парсера для языка. Примеры формализмов аналитической грамматики включают в себя следующее:

• Язык нисходящего анализа (TDPL): крайне минималистский формализм аналитической грамматики, разработанный в начале 1970-х годов для изучения поведения нисходящих анализаторов . ^[17]
• Грамматики связей : форма аналитической грамматики, разработанная для лингвистики , которая выводит синтаксическую структуру путем изучения позиционных отношений между парами слов. ^{[18] [19]}
• Грамматики выражений синтаксического анализа (PEG): более позднее обобщение TDPL, разработанное с учетом практических потребностей в выразительности разработчиков языков программирования и компиляторов . ^[20]

Смотрите также

• Абстрактное синтаксическое дерево
• Адаптивная грамматика
• Неоднозначная грамматика
• Форма Бэкуса–Наура (БНФ)
• Категориальная грамматика
• Конкретное синтаксическое дерево
• Расширенная форма Бэкуса-Наура (EBNF)
• Грамматика
• Грамматическая структура
• L-система
• Ложбан
• Постканоническая система
• Грамматика формы
• Правильно сформированная формула

Ссылки

1. Медуна, Александр (2014), Формальные языки и вычисления: модели и их приложения, CRC Press, стр. 233, ISBN 9781466513457. Более подробную информацию по этой теме см. в разделе неразрешимая проблема .
2. Chomsky, Noam (сентябрь 1956 г.). «Три модели описания языка». IRE Transactions on Information Theory . 2 (3): 113–124. doi :10.1109/TIT.1956.1056813. S2CID  19519474.
3. Хомский, Ноам (1957). Синтаксические структуры . Гаага: Мутон .
4. Ашаари, С.; Тураев, С.; Охунов, А. (2016). «Структурно и арифметически контролируемые грамматики» (PDF) . Международный журнал по перцептивным и когнитивным вычислениям . 2 (2): 27 . Получено 2024-11-05 .
5. Гинзбург, Сеймур (1975). Алгебраические и автоматные теоретические свойства формальных языков . Северная Голландия. С. 8–9. ISBN 978-0-7204-2506-2.
6. Харрисон, Майкл А. (1978). Введение в теорию формального языка . Рединг, Массачусетс: Addison-Wesley Publishing Company. стр. 13. ISBN 978-0-201-02955-0.
7. Формы предложений Архивировано 13 ноября 2019 г. в Wayback Machine , Контекстно-свободные грамматики, Дэвид Матушек
8. Грюн, Дик и Джейкобс, Сериэль Х., Методы анализа – практическое руководство , Эллис Хорвуд, Англия, 1990.
9. Эрли, Джей, «Эффективный алгоритм контекстно-свободного синтаксического анализа. Архивировано 19 мая 2020 г. на Wayback Machine », Communications of the ACM , том 13, № 2, стр. 94–102, февраль 1970 г.
10. Кнут, Д. Э. (июль 1965 г.). «О переводе языков слева направо». Информация и управление . 8 (6): 607–639. doi :10.1016/S0019-9958(65)90426-2.
11. Джоши, Аравинд К. и др. , «Грамматика на основе дерева», Журнал компьютерных систем , том 10, № 1, стр. 136-163, 1975.
12. Костер, Корнелис HA, «Аффиксные грамматики», в книге «Реализация ALGOL 68» , North Holland Publishing Company, Амстердам, стр. 95-109, 1971.
13. Кнут, Дональд Э., «Семантика контекстно-свободных языков», Математическая теория систем , т. 2 № 2, стр. 127-145, 1968.
14. Кнут, Дональд Э., «Семантика контекстно-свободных языков (исправление)», Математическая теория систем , т. 5, № 1, стр. 95-96, 1971.
15. Заметки о формальной теории языка и синтаксическом анализе. Архивировано 28 августа 2017 г. в Wayback Machine , Джеймс Пауэр, кафедра компьютерных наук Национального университета Ирландии, Мейнут, графство Килдэр, Ирландия.JPR02
16. Боренштейн, Сет (27 апреля 2006 г.). «Певчие птицы тоже понимают грамматику». Northwest Herald . стр. 2 – через Newspapers.com.
17. Бирман, Александр, Схема распознавания TMG , докторская диссертация, Принстонский университет, кафедра электротехники, февраль 1970 г.
18. Слейтор, Дэниел Д. и Темперли, Дэви, «Анализ английского языка с помощью связной грамматики», Технический отчет CMU-CS-91-196, Университет Карнеги-Меллона, компьютерные науки, 1991.
19. Слейтор, Дэниел Д. и Темперли, Дэви, «Анализ английского языка с помощью связной грамматики», Третий международный семинар по технологиям анализа , 1993. (Пересмотренная версия вышеуказанного отчета.)
20. Форд, Брайан, Пакрат. Анализ: практический линейный алгоритм с возвратом , магистерская диссертация, Массачусетский технологический институт, сентябрь 2002 г.

Внешние ссылки