Секретный обмен Шамира

Cryptographic algorithm created by Adi Shamir

Разделение секрета Шамира (SSS) — это эффективный алгоритм разделения секрета для распространения частной информации («секрета») среди группы. Секрет не может быть раскрыт, если кворум группы не объединит свои знания. Чтобы достичь этого, секрет математически делится на части («доли»), из которых секрет может быть собран заново только при объединении достаточного количества долей. SSS обладает свойством информационно-теоретической безопасности , что означает, что даже если злоумышленник украдет несколько долей, злоумышленник не сможет восстановить секрет, если он не украл количество долей кворума.

Разделение секрета Шамира используется в некоторых приложениях для совместного использования ключей доступа к главному секрету.

Объяснение высокого уровня

SSS используется для защиты секрета в распределенной форме, чаще всего для защиты ключей шифрования . Секрет делится на несколько частей, которые по отдельности не дают никакой информации о секрете.

Для восстановления секрета, защищенного SSS, необходимо некоторое количество акций, называемое порогом . Никакая информация о секрете не может быть получена из любого количества акций ниже порога (свойство, называемое совершенной секретностью ). В этом смысле SSS является обобщением одноразового блокнота (который можно рассматривать как SSS с порогом в два куска и двумя кусками в общей сложности). ^[1]

Пример применения

Компании необходимо защитить свое хранилище. Если код хранилища знает только один человек, код может быть утерян или недоступен, когда хранилище нужно будет открыть. Если код знают несколько человек, они могут не доверять друг другу и не всегда действовать честно.

В этой ситуации SSS может использоваться для генерации акций кода хранилища, которые распределяются среди уполномоченных лиц в компании. Минимальный порог и количество акций, предоставляемых каждому лицу, могут быть выбраны таким образом, чтобы хранилище было доступно только (группам) уполномоченных лиц. Если представлено меньше акций, чем порог, хранилище не может быть открыто.

Случайно, по принуждению или в качестве акта противодействия некоторые лица могут предоставить неверную информацию для своих акций. Если общее количество правильных акций не достигает минимального порога, хранилище остается заблокированным.

Варианты использования

Секретный обмен Шамира можно использовать для

• поделиться ключом для расшифровки корневого ключа менеджера паролей , ^[2]
• восстановить ключ пользователя для доступа к зашифрованной электронной почте ^[3] и
• поделитесь парольной фразой, используемой для воссоздания главного секрета, который в свою очередь используется для доступа к криптовалютному кошельку . ^[4]

Свойства и недостатки

SSS имеет полезные свойства, но также и недостатки ^[5] , которые означают, что он непригоден для некоторых видов использования.

Полезные свойства включают в себя:

1. Безопасность : схема имеет информационно-теоретическую безопасность .
2. Минимальный : размер каждой части не превышает размер исходных данных.
3. Расширяемость : для любого заданного порогового значения акции могут быть динамически добавлены или удалены, не затрагивая существующие акции.
4. Динамичность : безопасность можно повысить, не меняя секрет, а периодически изменяя полином (сохраняя тот же свободный член) и создавая новую долю для каждого из участников.
5. Гибкость : в организациях, где важна иерархия, каждому участнику может быть выдано разное количество акций в соответствии с его важностью в организации. Например, при пороге 3 президент может открыть сейф в одиночку, если ему дадут три акции, в то время как три секретаря, у каждого из которых есть по одной акции, должны объединить свои акции, чтобы открыть сейф.

К слабым сторонам относятся:

1. Нет проверяемого секретного обмена : В процессе повторной сборки акций SSS не предоставляет способа проверки правильности каждой используемой акции. Проверяемый секретный обмен направлен на проверку того, что акционеры честны и не предоставляют поддельные акции.
2. Единая точка отказа : Секрет должен существовать в одном месте, когда он делится на части, и снова в одном месте, когда он собирается заново. Это точки атаки, и другие схемы, включая мультиподпись, устраняют по крайней мере одну из этих единых точек отказа .

История

Ади Шамир , израильский ученый, впервые сформулировал эту схему в 1979 году. ^[6]

Математический принцип

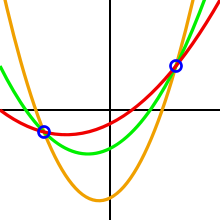
Схема использует теорему интерполяции Лагранжа , в частности, что точки на многочлене однозначно определяют многочлен степени , меньшей или равной . Например, 2 точек достаточно для определения прямой , 3 точек достаточно для определения параболы , 4 точек достаточно для определения кубической кривой и т. д. ${\displaystyle k}$ ${\displaystyle k-1}$

Математическая формулировка

Разделение секрета Шамира — это идеальная и совершенная пороговая схема , основанная на полиномиальной интерполяции по конечным полям . В такой схеме цель состоит в том, чтобы разделить секрет (например, комбинацию к сейфу ) на части данных (известные как доли ) таким образом, чтобы: ${\displaystyle \left(k,n\right)}$ ${\displaystyle S}$ ${\displaystyle n}$ ${\displaystyle S_{1},\ldots ,S_{n}}$

1. Знание любой или нескольких долей делает вычислимым. То есть, весь секрет может быть восстановлен из любой комбинации долей. ${\displaystyle k}$ ${\displaystyle S_{i}}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle k}$
2. Знание любого или меньшего количества акций оставляет полностью неопределенным, в том смысле, что возможные значения для остаются столь же вероятными при знании до акций, как и при знании акций. Секрет не может быть восстановлен при меньшем количестве акций. ${\displaystyle k-1}$ ${\displaystyle S_{i}}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle k-1}$ ${\displaystyle 0}$ ${\displaystyle S}$ ${\displaystyle k}$

Если , то для восстановления секрета необходимы все доли . ${\displaystyle n=k}$ ${\displaystyle S}$

Можно нарисовать бесконечное количество многочленов степени 2 через 2 точки. Для однозначного определения многочлена степени 2 требуются 3 точки. Это изображение приведено только для иллюстрации — схема Шамира использует многочлены над конечным полем, которые нелегко представить на двумерной плоскости.

Предположим, что секрет может быть представлен как элемент конечного поля ( где больше, чем число генерируемых акций). Случайным образом выбираем элементы, , из и строим многочлен . Вычисляем любые точки на кривой, например, устанавливаем для поиска точек . Каждому участнику дана точка (ненулевой вход для многочлена и соответствующий выход). ^[7] Учитывая любое подмножество этих пар, можно получить с помощью интерполяции , причем одной из возможных формул для этого является , где список точек многочлена задан как пары вида . Обратите внимание, что равно первому коэффициенту многочлена . ${\displaystyle S}$ ${\displaystyle a_{0}}$ ${\displaystyle \mathrm {GF} (q)}$ ${\displaystyle q}$ ${\displaystyle n}$ ${\displaystyle k-1}$ ${\displaystyle a_{1},\cdots ,a_{k-1}}$ ${\displaystyle \mathrm {GF} (q)}$ ${\displaystyle f\left(x\right)=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{k-1}x^{k-1}}$ ${\displaystyle n}$ ${\displaystyle i=1,\ldots ,n}$ ${\displaystyle \left(i,f\left(i\right)\right)}$ ${\displaystyle k}$ ${\displaystyle a_{0}}$ ${\displaystyle a_{0}=f(0)=\sum _{j=0}^{k-1}y_{j}\prod _{\begin{smallmatrix}m\,=\,0\\m\,\neq \,j\end{smallmatrix}}^{k-1}{\frac {x_{m}}{x_{m}-x_{j}}}}$ ${\displaystyle k}$ ${\displaystyle (x_{i},y_{i})}$ ${\displaystyle f(0)}$ ${\displaystyle f(x)}$

Пример расчета

Следующий пример иллюстрирует основную идею. Обратите внимание, однако, что вычисления в примере производятся с использованием целочисленной арифметики, а не арифметики конечных полей, чтобы сделать идею более понятной. Поэтому пример ниже не обеспечивает идеальной секретности и не является надлежащим примером схемы Шамира. Следующий пример объяснит проблему.

Подготовка

Предположим, что секрет, которым нужно поделиться, — 1234 . ${\displaystyle (S=1234)}$

В этом примере секрет будет разделен на 6 частей , где любой поднабор из 3 частей достаточен для восстановления секрета. числа берутся случайным образом. Пусть это будут 166 и 94. ${\displaystyle (n=6)}$ ${\displaystyle (k=3)}$ ${\displaystyle k-1=2}$

Это дает коэффициенты, где находится секрет ${\displaystyle (a_{0}=1234;a_{1}=166;a_{2}=94),}$ ${\displaystyle a_{0}}$

Таким образом, полином для получения секретных долей (точек) имеет вид:

${\displaystyle f(x)=1234+166x+94x^{2}}$

Шесть точек из полинома строятся как: ${\displaystyle D_{x-1}=(x,f(x))}$

${\displaystyle D_{0}=(1,1494);D_{1}=(2,1942);D_{2}=(3,2578);D_{3}=(4,3402);D_{4}=(5,4414);D_{5}=(6,5614)}$

Каждый участник схемы получает разную точку (пару и ). Поскольку вместо точек начинаются с и не используется . Это необходимо, поскольку это секрет. ${\displaystyle x}$ ${\displaystyle f(x)}$ ${\displaystyle D_{x-1}}$ ${\displaystyle D_{x}}$ ${\displaystyle (1,f(1))}$ ${\displaystyle (0,f(0))}$ ${\displaystyle f(0)}$

Реконструкция

Для того, чтобы восстановить секрет, достаточно любых 3 точек.

Рассмотрите возможность использования 3-х точек . ${\displaystyle \left(x_{0},y_{0}\right)=\left(2,1942\right);\left(x_{1},y_{1}\right)=\left(4,3402\right);\left(x_{2},y_{2}\right)=\left(5,4414\right)}$

Вычисление базисных полиномов Лагранжа :

${\displaystyle \ell _{0}(x)={\frac {x-x_{1}}{x_{0}-x_{1}}}\cdot {\frac {x-x_{2}}{x_{0}-x_{2}}}={\frac {x-4}{2-4}}\cdot {\frac {x-5}{2-5}}={\frac {1}{6}}x^{2}-{\frac {3}{2}}x+{\frac {10}{3}}}$

${\displaystyle \ell _{1}(x)={\frac {x-x_{0}}{x_{1}-x_{0}}}\cdot {\frac {x-x_{2}}{x_{1}-x_{2}}}={\frac {x-2}{4-2}}\cdot {\frac {x-5}{4-5}}=-{\frac {1}{2}}x^{2}+{\frac {7}{2}}x-5}$

${\displaystyle \ell _{2}(x)={\frac {x-x_{0}}{x_{2}-x_{0}}}\cdot {\frac {x-x_{1}}{x_{2}-x_{1}}}={\frac {x-2}{5-2}}\cdot {\frac {x-4}{5-4}}={\frac {1}{3}}x^{2}-2x+{\frac {8}{3}}}$

Используя формулу полиномиальной интерполяции, получим: ${\displaystyle f(x)}$

${\displaystyle {\begin{aligned}f(x)&=\sum _{j=0}^{2}y_{j}\cdot \ell _{j}(x)\\[6pt]&=y_{0}\ell _{0}(x)+y_{1}\ell _{1}(x)+y_{2}\ell _{2}(x)\\[6pt]&=1942\left({\frac {1}{6}}x^{2}-{\frac {3}{2}}x+{\frac {10}{3}}\right)+3402\left(-{\frac {1}{2}}x^{2}+{\frac {7}{2}}x-5\right)+4414\left({\frac {1}{3}}x^{2}-2x+{\frac {8}{3}}\right)\\[6pt]&=1234+166x+94x^{2}\end{aligned}}}$

Напоминая, что секрет — это свободный коэффициент, а это значит, что , и секрет восстановлен. ${\displaystyle S=1234}$

Вычислительно эффективный подход

Использование полиномиальной интерполяции для нахождения коэффициента в исходном полиноме с использованием полиномов Лагранжа неэффективно , поскольку вычисляются неиспользуемые константы. ${\displaystyle S=f(0)}$

Учитывая это, оптимизированная формула для использования полиномов Лагранжа для нахождения определяется следующим образом: ${\displaystyle f(0)}$

${\displaystyle f(0)=\sum _{j=0}^{k-1}y_{j}\prod _{\begin{smallmatrix}m\,=\,0\\m\,\neq \,j\end{smallmatrix}}^{k-1}{\frac {x_{m}}{x_{m}-x_{j}}}}$

Проблема использования целочисленной арифметики

Хотя упрощенная версия метода, продемонстрированная выше, которая использует целочисленную арифметику вместо арифметики конечных полей, работает, существует проблема безопасности: Ева получает информацию о каждом найденном элементе. ${\displaystyle S}$ ${\displaystyle D_{i}}$

Предположим, что она находит 2 точки и . У нее по-прежнему нет точек, поэтому теоретически она не должна была получить больше информации о . Но она могла бы объединить информацию из 2 точек с общедоступной информацией: . Сделав это, Ева могла бы выполнить следующую алгебру: ${\displaystyle D_{0}=(1,1494)}$ ${\displaystyle D_{1}=(2,1942)}$ ${\displaystyle k=3}$ ${\displaystyle S}$ ${\displaystyle n=6,k=3,f(x)=a_{0}+a_{1}x+\cdots +a_{k-1}x^{k-1},a_{0}=S,a_{i}\in \mathbb {Z} }$

1. Заполните формулу для и значение ${\displaystyle f(x)}$ ${\displaystyle S}$ ${\displaystyle k:f(x)=S+a_{1}x+\cdots +a_{k-1}x^{k-1}\Rightarrow {}f(x)=S+a_{1}x+a_{2}x^{2}}$
2. Заполните (1) значениями 's и ${\displaystyle D_{0}}$ ${\displaystyle x}$ ${\displaystyle f(x):1494=S+a_{1}1+a_{2}1^{2}\Rightarrow {}1494=S+a_{1}+a_{2}}$
3. Заполните (1) значениями 's и ${\displaystyle D_{1}}$ ${\displaystyle x}$ ${\displaystyle f(x):1942=S+a_{1}2+a_{2}2^{2}\Rightarrow {}1942=S+2a_{1}+4a_{2}}$
4. Вычтите (3)-(2): и перепишите это как . ${\displaystyle (1942-1494)=(S-S)+(2a_{1}-a_{1})+(4a_{2}-a_{2})\Rightarrow {}448=a_{1}+3a_{2}}$ ${\displaystyle a_{1}=448-3a_{2}}$
5. Теперь Ева может заменить результат из (4) на (2): что приводит ее к информации о том, что S — четное число. ${\displaystyle 1494=S+(448-3a_{2})+a_{2}\Rightarrow {}S=1046+2a_{2}}$

Решение с использованием арифметики конечного поля

Это полиномиальная кривая над конечным полем — порядок полинома, по-видимому, мало связан с формой графика.

Вышеуказанная атака использует ограничения на значения, которые может принимать полином в силу того, как он был построен: полином должен иметь коэффициенты, являющиеся целыми числами, и полином должен принимать целое число в качестве значения при оценке в каждой из координат, используемых в схеме. Это уменьшает его возможные значения в неизвестных точках, включая результирующий секрет, учитывая меньше, чем акций. ${\displaystyle k}$

Эту проблему можно решить, используя арифметику конечного поля. Конечное поле всегда имеет размер , где — простое число, а — положительное целое число. Размер поля должен удовлетворять , и это больше, чем количество возможных значений секрета, хотя последнее условие можно обойти, разделив секрет на меньшие секретные значения и применив схему к каждому из них. В нашем примере ниже мы используем простое поле (т. е. r = 1). На рисунке показана полиномиальная кривая над конечным полем. ${\displaystyle q=p^{r}}$ ${\displaystyle p}$ ${\displaystyle r}$ ${\displaystyle q}$ ${\displaystyle q>n}$ ${\displaystyle q}$

На практике это лишь небольшое изменение. Порядок q поля (т. е. количество значений, которые оно имеет) должен быть выбран больше, чем количество участников и количество значений, которые может принимать секрет. Все вычисления, включающие полином, также должны быть вычислены над полем (mod p в нашем примере, где берется как простое число), а не над целыми числами. Как выбор поля, так и отображение секрета на значение в этом поле считаются публично известными. ${\displaystyle a_{0}=S}$ ${\displaystyle p=q}$

Для этого примера выберите , тогда многочлен примет вид , который дает точки: ${\displaystyle p=1613}$ ${\displaystyle f(x)=1234+166x+94x^{2}{\bmod {1613}}}$ ${\displaystyle (1,1494);(2,329);(3,965);(4,176);(5,1188);(6,775)}$

На этот раз Ева не получает никакой информации, когда находит (пока у нее нет очков). ${\displaystyle D_{x}}$ ${\displaystyle k}$

Предположим снова, что Ева находит и , а общедоступная информация: . Пытаясь выполнить предыдущую атаку, Ева может: ${\displaystyle D_{0}=\left(1,1494\right)}$ ${\displaystyle D_{1}=\left(2,329\right)}$ ${\displaystyle n=6,k=3,p=1613,f(x)=a_{0}+a_{1}x+\dots +a_{k-1}x^{k-1}\mod {p},a_{0}=S,a_{i}\in \mathbb {N} }$

1. Заполните формулу и значением и : ${\displaystyle f(x)}$ ${\displaystyle S}$ ${\displaystyle k}$ ${\displaystyle p}$ ${\displaystyle f(x)=S+a_{1}x+\dots +a_{3-1}x^{3-1}\mod 1613}$
2. Заполните (1) значениями 's и ${\displaystyle D_{0}}$ ${\displaystyle x}$ ${\displaystyle f(x):1494\equiv S+a_{1}1+a_{2}1^{2}{\pmod {1613}}\Rightarrow {}1494\equiv S+a_{1}+a_{2}{\pmod {1613}}}$
3. Заполните (1) значениями 's и ${\displaystyle D_{1}}$ ${\displaystyle x}$ ${\displaystyle f(x):1942\equiv S+a_{1}2+a_{2}2^{2}{\pmod {1613}}\Rightarrow {}1942\equiv S+2a_{1}+4a_{2}{\pmod {1613}}}$
4. Вычтите (3)-(2): и перепишите это как ${\displaystyle (1942-1494)\equiv (S-S)+(2a_{1}-a_{1})+(4a_{2}-a_{2}){\pmod {1613}}\Rightarrow {}448\equiv a_{1}+3a_{2}{\pmod {1613}}}$ ${\displaystyle a_{1}\equiv 448-3a_{2}{\pmod {1613}}}$

Существуют возможные значения для . Она знает, что всегда уменьшается на 3, поэтому если делится на , она могла бы заключить . Однако является простым числом, поэтому она не может заключить это. Таким образом, использование конечного поля позволяет избежать этой возможной атаки. ${\displaystyle p}$ ${\displaystyle a_{1}}$ ${\displaystyle [448,445,442,\ldots ]}$ ${\displaystyle p}$ ${\displaystyle 3}$ ${\displaystyle a_{1}\in [1,4,7,\ldots ]}$ ${\displaystyle p}$

Кроме того, хотя Ева может заключить, что , это не дает никакой дополнительной информации, поскольку «циклическое» поведение модульной арифметики предотвращает утечку «S четно», в отличие от примера с целочисленной арифметикой выше. ${\displaystyle S\equiv 1046+2a_{2}{\pmod {1613}}}$

Код Python

Для большей ясности кода здесь используется простое поле. На практике для удобства схема, построенная с использованием меньшего двоичного поля, может быть отдельно применена к небольшим подстрокам битов секрета (например, GF(256) для побайтового применения) без потери безопасности. Строгое условие, что размер поля должен быть больше количества акций, все равно должно соблюдаться (например, если количество акций может превысить 255, поле GF(256) может быть заменено, скажем, на GF(65536)).

""" Следующая реализация Python для разделения секрета Шамира передается в общественное достояние на условиях CC0 и OWFa: https://creativecommons.org/publicdomain/zero/1.0/ http://www.openwebfoundation.org/legal/the-owf-1-0-agreements/owfa-1-0См. несколько нижних строк для использования. Протестировано на Python 2 и 3. """из  __future__  импортировать  подразделение из  __future__  импортировать  функцию_печатиимпорт  случайный импорт  functools# 12-й Мерсенн Прайм _PRIME  =  2  **  127  -  1_RINT  =  functools.partial ( random.SystemRandom ( ) . randint , 0 )​​​ def  _eval_at ( poly ,  x ,  prime ): """Оценивает полином (кортеж коэффициентов) при x, используемый для генерации  пула Шамира в make_random_shares ниже.  """ accum = 0 для coeff в reversed ( poly ): accum *= x accum += coeff accum %= prime return accum                   def  make_random_shares ( secret ,  minimum ,  shares ,  prime = _PRIME ): """  Генерирует случайный пул Шамира для заданного секрета, возвращает баллы шар.  """ если минимум > шар : raise ValueError ( "Секрет пула будет невосстановим." ) poly = [ secret ] + [ _RINT ( prime - 1 ) for i in range ( minimum - 1 )] points = [( i , _eval_at ( poly , i , prime )) for i in range ( 1 , shares + 1 )] return баллы                                   def  _extended_gcd ( a ,  b ): """  Деление целых чисел по модулю p означает нахождение обратной величины  знаменателя по модулю p и последующее умножение числителя на эту  обратную величину (Примечание: обратная величина для A — это B, такая что A*B % p == 1). Это можно  вычислить с помощью расширенного алгоритма Евклида  http://en.wikipedia.org/wiki/Shamir%27s_Secret_Sharing/Modular_multiplicative_inverse#Computation  """ x = 0 last_x = 1 y = 1 last_y = 0 while b != 0 : quot = a // b a , b = b , a % b x , last_x = last_x - quot * x , x y , last_y = last_y - quot * y , y return last_x , last_y                                                  def  _divmod ( num ,  den ,  p ): """Вычислить число/день по модулю простого числа p  Чтобы объяснить это, результат будет таким:  den * _divmod(num, den, p) % p == num  """  inv ,  _  =  _extended_gcd ( den ,  p )  return  num  *  invdef  _lagrange_interpolate ( x ,  x_s ,  y_s ,  p ): """  Найти значение y для заданного x, заданных n (x, y) точек;  k точек определят полином до k-го порядка.  """ k = len ( x_s ) assert k == len ( set ( x_s )), "точки должны быть различными" def PI ( vals ): # заглавная буква PI — произведение входных данных accum = 1 for v in vals : accum *= v return accum nums = [ ] # избежать неточного деления dens = [] for i in range ( k ) : others = list ( x_s ) cur = others.pop ( i ) nums.append ( PI ( x - o for o in others )) dens . append ( PI ( cur - o for o in others )) den = PI ( dens ) num = sum ([ _divmod ( nums [ i ] * den * y_s [ i ] % p , dens [ i ], p ) for i in range ( k )]) return ( _divmod ( num , den , p ) + p ) % p                                                                                 def  recovery_secret ( shares ,  prime = _PRIME ): """  Восстановить секрет из общих точек  (точек (x,y) на полиноме).  """ if len ( shares ) < 3 : raise ValueError ( "нужно не менее трех общих частей" ) x_s , y_s = zip ( * общие части ) return _lagrange_interpolate ( 0 , x_s , y_s , prime )                def  main (): """Основная функция""" секрет = 1234 доли = make_random_shares ( секрет , минимум = 3 , доли = 6 )          print ( 'Секрет:' ,  секрет )  print ( 'Доли:' )  если  доли :  для  доли  в  долях :  print ( ' ' ,  доля ) print ( 'Секрет, восстановленный из минимального подмножества акций: ' ,  recovery_secret ( shares [: 3 ]))  print ( 'Секрет, восстановленный из другого минимального подмножества акций: ' ,  recovery_secret ( shares [ - 3 :]))если  __name__  ==  '__main__' :  main ()

Смотрите также

• Секретный обмен
• Безопасные многосторонние вычисления
• Полином Лагранжа
• Гомоморфное разделение секрета – упрощенный децентрализованный протокол голосования
• Правило двух человек
• Частичный пароль

Ссылки

1. Кренн, Стефан; Лоруенсер, Томас (2023). Введение в разделение секрета: систематический обзор и руководство по выбору протокола . doi : 10.1007/978-3-031-28161-7. ISBN 978-3-031-28160-0.
2. "Запечатать/Распечатать". Хранилище HashiCorp . Получено 2022-10-02 .
3. "PreVeil Review". PCMag . Получено 2022-10-02 .
4. Руснак, Павол; Козлик, Эндрю; Вейпустек, Ондрей; Сусанка, Томаш; Палатинус, Марек; Хёнике, Йохен (18.12.2017). "SLIP-0039: Разделение секрета Шамира для мнемонических кодов". GitHub . SatoshiLabs . Получено 03.10.2022 . Этот SLIP описывает стандартную и совместимую реализацию разделения секрета Шамира (SSS) и спецификацию для его использования при резервном копировании иерархических детерминированных кошельков, описанных в BIP-0032.
5. Лопп, Джеймсон (2020-10-01). "Недостатки разделения секрета Шамира" . Получено 2022-10-03 . Разновидности разделения секрета Шамира (SSS) были реализованы несколько раз в сфере криптовалют, но позже разработчики поняли, что дополнительная сложность в конечном итоге снизила безопасность системы.
6. Шамир, Ади (1979), «Как поделиться секретом», Сообщения ACM , 22 (11): 612–613, doi : 10.1145/359168.359176 , S2CID  16321225
7. Кнут, Д.Э. (1997), Искусство программирования , т. II: Получисленные алгоритмы (3-е изд.), Addison-Wesley, стр. 505.

Дальнейшее чтение

• Доусон, Э.; Донован, Д. (1994), «Широта схемы Шамира по разделению секретов», Компьютеры и безопасность , 13 : 69–78, doi :10.1016/0167-4048(94)90097-3.
• Benzekki, K. (2017). «Проверяемый подход к разделению секрета для безопасного хранения в MultiCloud». Ubiquitous Networking . Lecture Notes in Computer Science. Vol. 10542. Casablanca: Springer. pp. 225–234. doi :10.1007/978-3-319-68179-5_20. ISBN 978-3-319-68178-8..

Внешние ссылки

• Секретный обмен Шамира в библиотеке Crypto++
• Схема обмена секретами Шамира (ssss) – реализация GNU GPL
• sharedsecret – реализация на Go
• s4 - онлайн-инструмент для обмена секретами Шамира, использующий алгоритм обмена секретами Шамира от HashiCorp
• Shamir39 - веб-версия на iancoleman.io
• kn Secrets — веб-версия на специальном сайте, призванная сделать секретную информацию Шамира максимально доступной