Рассеяние света частицами — это процесс, при котором мелкие частицы (например, ледяные кристаллы , пыль , атмосферные частицы , космическая пыль и клетки крови ) рассеивают свет, вызывая оптические явления, такие как голубой цвет неба и гало .
Уравнения Максвелла являются основой теоретических и вычислительных методов, описывающих рассеяние света , но поскольку точные решения уравнений Максвелла известны только для определенных геометрий частиц (например, сферических), рассеяние света частицами является разделом вычислительной электродинамики, изучающим рассеяние и поглощение электромагнитного излучения частицами.
В случае геометрий , для которых известны аналитические решения (таких как сферы , кластеры сфер, бесконечные цилиндры ), решения обычно вычисляются в терминах бесконечных рядов . В случае более сложных геометрий и для неоднородных частиц исходные уравнения Максвелла дискретизируются и решаются . Эффекты многократного рассеяния света частицами обрабатываются методами переноса излучения (см., например, коды переноса излучения в атмосфере ).
Относительный размер рассеивающей частицы определяется ее параметром размера x , который представляет собой отношение ее характерного размера к длине волны :
Метод FDTD принадлежит к общему классу методов численного моделирования во временной области на основе сеток с дифференциальным распределением. Зависящие от времени уравнения Максвелла (в форме частных производных) дискретизируются с использованием центрально-разностных приближений к пространственным и временным частным производным. Полученные конечно-разностные уравнения решаются либо программным, либо аппаратным способом скачком: компоненты вектора электрического поля в объеме пространства решаются в заданный момент времени; затем компоненты вектора магнитного поля в том же пространственном объеме решаются в следующий момент времени; и процесс повторяется снова и снова, пока желаемое переходное или стационарное поведение электромагнитного поля не будет полностью развито.
Этот метод также известен как метод нулевого поля и метод расширенной границы (EBCM). Матричные элементы получаются путем сопоставления граничных условий для решений уравнений Максвелла. Падающее, прошедшее и рассеянное поле разлагаются в сферические векторные волновые функции.
Рассеяние от любых сферических частиц с произвольным параметром размера объясняется теорией Ми . Теория Ми, также называемая теорией Лоренца-Ми или теорией Лоренца-Ми-Дебая, представляет собой полное аналитическое решение уравнений Максвелла для рассеяния электромагнитного излучения сферическими частицами (Борен и Хаффман, 1998).
Для более сложных форм, таких как покрытые сферы, мультисферы, сфероиды и бесконечные цилиндры, существуют расширения, которые выражают решение в терминах бесконечных серий. Существуют коды, доступные для изучения рассеяния света в приближении Ми для сфер, слоистых сфер и множественных сфер и цилиндров .
Существует несколько методов расчета рассеяния излучения частицами произвольной формы. Дискретное дипольное приближение представляет собой приближение непрерывной цели конечным массивом поляризуемых точек. Точки приобретают дипольные моменты в ответ на локальное электрическое поле. Диполи этих точек взаимодействуют друг с другом через свои электрические поля. Существуют коды DDA для расчета свойств рассеяния света в приближении DDA.
Режим рэлеевского рассеяния — это рассеяние света или другого электромагнитного излучения частицами, размер которых намного меньше длины волны света. Рэлеевское рассеяние можно определить как рассеяние в режиме малых параметров размера .
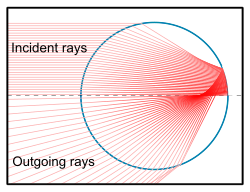
Методы трассировки лучей могут аппроксимировать рассеяние света не только сферическими частицами, но и частицами любой заданной формы (и ориентации), пока размер и критические размеры частицы намного больше длины волны света. Свет можно рассматривать как совокупность лучей, ширина которых намного больше длины волны, но мала по сравнению с самой частицей. Каждый луч, падающий на частицу, может претерпеть (частичное) отражение и/или преломление. Эти лучи выходят в направлениях, таким образом, вычисляемых с их полной мощностью или (когда задействовано частичное отражение) с падающей мощностью, разделенной между двумя (или более) выходящими лучами. Так же, как в случае линз и других оптических компонентов, трассировка лучей определяет свет, исходящий от одного рассеивателя, и, статистически объединяя этот результат для большого количества случайно ориентированных и расположенных рассеивателей, можно описать атмосферные оптические явления, такие как радуги из-за капель воды и гало из-за ледяных кристаллов. Существуют доступные коды трассировки лучей для атмосферной оптики .