Реактор с непрерывным перемешиванием

Тип химического реактора

Схема, показывающая установку реактора непрерывного действия с мешалкой

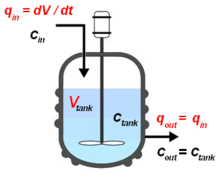
Непрерывный реактор с перемешиванием ( CSTR ), также известный как реактор с чановым или обратным смешением , реактор со смешанным потоком ( MFR ) или реактор с перемешиванием непрерывного потока ( CFSTR ), является распространенной моделью химического реактора в химической инженерии и инженерии окружающей среды . CSTR часто относится к модели, используемой для оценки ключевых переменных работы установки при использовании непрерывного реактора с перемешиванием для достижения заданного выхода. Математическая модель работает для всех сред: жидкостей, газов и суспензий .

Поведение CSTR часто аппроксимируется или моделируется поведением идеального CSTR, которое предполагает идеальное смешивание . В идеально смешанном реакторе реагент мгновенно и равномерно смешивается по всему реактору при входе. Следовательно, выходной состав идентичен составу материала внутри реактора, который является функцией времени пребывания и скорости реакции. CSTR является идеальным пределом полного смешивания в конструкции реактора, что является полной противоположностью реактору с поршневым потоком ( PFR). На практике ни один реактор не ведет себя идеально, а вместо этого находится где-то между пределами смешивания идеального CSTR и PFR.

Идеальный CSTR

Поперечный разрез CSTR

Моделирование

Непрерывный поток жидкости, содержащий неконсервативный химический реагент А, поступает в идеальный CSTR объемом V.

Предположения:

• идеальное или идеальное смешивание
• стационарное состояние , где N _A — число молей вида A ${\displaystyle {\Bigl (}{\frac {dN_{A}}{dt}}=0{\Bigr )}}$
• закрытые границы
• постоянная плотность жидкости (действительно для большинства жидкостей; действительно для газов только в том случае, если нет чистого изменения числа молей или резкого изменения температуры)
• Реакция n- ^го порядка ( r = kC _A ⁿ ), где k — константа скорости реакции, C _A — концентрация вещества A, а n — порядок реакции.
• изотермические условия или постоянная температура ( k постоянна)
• одиночная, необратимая реакция ( ν _A = −1)
• Все реагенты А превращаются в продукты посредством химической реакции
• Н _А = С _А В

Интегральный баланс масс по числу молей N _A вида A в реакторе объемом V : ${\displaystyle 1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]}$

${\displaystyle 2.{\frac {dN_{A}}{dt}}=F_{Ao}-F_{A}+V\nu _{A}r_{A}}$^[1]

где

• F _Ao — молярный расход на входе вида A
• F _A - молярный расход на выходе вида A
• v _A — стехиометрический коэффициент
• r _A — скорость реакции

Применяя предположения об устойчивом состоянии и ν _A = −1, уравнение 2 упрощается до:

${\displaystyle 3.\ 0=F_{Ao}-F_{A}-Vr_{A}}$

Молярные скорости потока вида A затем можно переписать через концентрацию A и скорость потока жидкости ( Q ):

${\displaystyle 4.\ 0=QC_{Ao}-QC_{A}-Vr_{A}}$^[2]

Уравнение 4 можно затем перестроить, чтобы выделить r _A и упростить:

${\displaystyle 5.\ r_{A}={\frac {Q}{V}}(C_{Ao}-C_{A})}$^[2]

${\displaystyle 6.\ r_{A}={\frac {1}{\tau }}(C_{Ao}-C_{A})}$

где

• ${\displaystyle \tau }$теоретическое время пребывания ( ) ${\displaystyle \tau ={\tfrac {V}{Q}}}$
• C _Ao — концентрация вида A на входе
• C _A — концентрация вида A на выходе из реактора

Время пребывания — это общее количество времени, которое дискретное количество реагента проводит внутри реактора. Для идеального реактора теоретическое время пребывания, , всегда равно объему реактора, деленному на скорость потока жидкости. ^[2] Более подробное обсуждение распределения времени пребывания CSTR см. в следующем разделе. ${\displaystyle \tau }$

В зависимости от порядка реакции , скорость реакции, r _A , как правило, зависит от концентрации видов A в реакторе и константы скорости. Ключевым предположением при моделировании CSTR является то, что любой реагент в жидкости идеально (т. е. равномерно) смешан в реакторе, что подразумевает, что концентрация внутри реактора такая же, как и в выходном потоке. ^[3] Константу скорости можно определить, используя известную эмпирическую скорость реакции, которая скорректирована с учетом температуры с помощью температурной зависимости Аррениуса . ^[2] Как правило, с ростом температуры увеличивается и скорость, с которой происходит реакция.

Уравнение 6 можно решить путем интегрирования после подстановки соответствующего выражения скорости. В таблице ниже приведены выходные концентрации видов A для идеального CSTR. Значения выходной концентрации и времени пребывания являются основными критериями проектирования при проектировании CSTR для промышленного применения.

Распределение времени пребывания

Функции распределения возраста выхода E(t) и кумулятивного распределения возраста F(t) для идеального CSTR

Идеальный CSTR будет демонстрировать четко определенное поведение потока, которое можно охарактеризовать распределением времени пребывания в реакторе или распределением возраста на выходе. ^[4] Не все частицы жидкости будут проводить одинаковое количество времени внутри реактора. Распределение возраста на выходе (E(t)) определяет вероятность того, что данная частица жидкости проведет время t в реакторе. Аналогично, кумулятивное распределение возраста (F(t)) дает вероятность того, что данная частица жидкости имеет возраст на выходе меньше времени t. ^[3] Одним из ключевых выводов из распределения возраста на выходе является то, что очень небольшое количество частиц жидкости никогда не покинет CSTR. ^[5] В зависимости от применения реактора это может быть как преимуществом, так и недостатком.

Неидеальный CSTR

Хотя идеальная модель CSTR полезна для прогнозирования судьбы компонентов во время химического или биологического процесса, CSTR редко демонстрируют идеальное поведение в реальности. ^[2] Чаще всего гидравлика реактора не ведет себя идеально или условия системы не подчиняются первоначальным предположениям. Идеальное смешивание — это теоретическая концепция, которая недостижима на практике. ^[6] Однако для инженерных целей, если время пребывания в 5–10 раз превышает время смешивания, предположение об идеальном смешении обычно остается верным.

Функции распределения возраста выхода E(t) и кумулятивного распределения возраста F(t) для CSTR с мертвым пространством

Неидеальное гидравлическое поведение обычно классифицируется либо как мертвое пространство, либо как короткое замыкание. Эти явления возникают, когда некоторая жидкость проводит меньше времени в реакторе, чем теоретическое время пребывания, . Наличие углов или перегородок в реакторе часто приводит к появлению некоторого мертвого пространства, где жидкость плохо перемешивается. ^[6] Аналогично, струя жидкости в реакторе может вызвать короткое замыкание, при котором часть потока выходит из реактора намного быстрее, чем основная часть жидкости. Если мертвое пространство или короткое замыкание происходит в CSTR, соответствующие химические или биологические реакции могут не завершиться до того, как жидкость выйдет из реактора. ^[2] Любое отклонение от идеального потока приведет к распределению времени пребывания, отличному от идеального распределения, как показано справа. ${\displaystyle \tau }$

Моделирование неидеального потока

Хотя идеальные проточные реакторы редко встречаются на практике, они являются полезными инструментами для моделирования неидеальных проточных реакторов. Любой режим потока может быть достигнут путем моделирования реактора как комбинации идеальных CSTR и реакторов поршневого потока (PFR) либо последовательно, либо параллельно. ^[6] Например, бесконечная серия идеальных CSTR гидравлически эквивалентна идеальному PFR. ^[2] Модели реакторов, объединяющие несколько CSTR последовательно, часто называют моделями tank-in-series (TIS). ^[7]

Для моделирования систем, которые не подчиняются предположениям о постоянной температуре и единственной реакции, необходимо учитывать дополнительные зависимые переменные. Если система считается находящейся в нестационарном состоянии, необходимо решить дифференциальное уравнение или систему связанных дифференциальных уравнений. Отклонения поведения CSTR могут быть рассмотрены с помощью дисперсионной модели. Известно, что CSTR являются одной из систем, демонстрирующих сложное поведение, такое как множественность стационарного состояния, предельные циклы и хаос.

Каскады CSTR

Серия из трех CSTR

Каскады CSTR, также известные как серии CSTR, используются для уменьшения громкости системы. ^[8]

Минимизация громкости

По мере увеличения количества последовательно соединенных CSTR общий объем реактора уменьшается.

Как видно на графике с одним CSTR, где обратная скорость отображена как функция фракционной конверсии , площадь в рамке равна , где V — общий объем реактора, а — молярная скорость потока сырья. Когда тот же процесс применяется к каскаду CSTR, как показано на графике с тремя CSTR, объем каждого реактора рассчитывается из каждой входной и выходной фракционной конверсии, что приводит к уменьшению общего объема реактора. Оптимальный размер достигается, когда площадь над прямоугольниками от CSTR в серии, которая ранее была покрыта одним CSTR, максимизируется. Для реакции первого порядка с двумя CSTR следует использовать равные объемы. Поскольку количество идеальных CSTR (n) приближается к бесконечности, общий объем реактора приближается к идеальному PFR для той же реакции и фракционной конверсии. ${\displaystyle {\frac {V}{F_{Ao}}}}$ ${\displaystyle F_{Ao}}$

Идеальный каскад CSTR

Из уравнения расчета одного CSTR, где , мы можем определить, что для одного CSTR, соединенного последовательно, , где — время в реакторе, — концентрация сырья A, — концентрация сырья A на выходе, — скорость реакции A. ${\displaystyle \tau ={\frac {C_{Ao}-C_{A}}{-r_{A}}}}$ ${\displaystyle \tau _{i}={\frac {C_{A(i-1)}-C_{Ai}}{-r_{Ai}}}}$ ${\displaystyle \tau }$ ${\displaystyle C_{Ao}}$ ${\displaystyle C_{A}}$ ${\displaystyle -r_{A}}$

Первый заказ

Для изотермической реакции первого порядка с постоянной плотностью в каскаде идентичных CSTR, работающих в стационарном состоянии

Для одного CSTR: , где k — константа скорости , а — выходная концентрация A из первого CSTR ${\displaystyle C_{A1}={\frac {C_{Ao}}{1+k\tau }}}$ ${\displaystyle C_{A1}}$

Два CSTR: и ${\displaystyle C_{A1}={\frac {C_{Ao}}{1+k\tau }}}$ ${\displaystyle C_{A2}={\frac {C_{A1}}{1+k\tau }}}$

Подставляем первое уравнение CSTR во второе: ${\displaystyle C_{A2}={\frac {C_{Ao}}{(1+k\tau )^{2}}}}$

Следовательно, для m идентичных CSTR, соединенных последовательно: ${\displaystyle C_{Am}={\frac {C_{Ao}}{(1+k\tau )^{m}}}}$

Когда объемы отдельных CSTR в серии меняются, порядок CSTR не изменяет общую конверсию для реакции первого порядка, пока CSTR работают при одной и той же температуре.

Нулевой порядок

В стационарном состоянии общее уравнение для изотермической реакции нулевого порядка в каскаде CSTR имеет вид ${\displaystyle C_{Am}=C_{Ao}-\sum _{i=1}^{m}k_{i}\tau _{i}}$

Когда каскад CSTR является изотермическим с идентичными реакторами, концентрация определяется выражением ${\displaystyle C_{Am}=C_{Ao}-mk_{i}\tau _{i}}$

Второго порядка

Для изотермической реакции второго порядка в стационарном состоянии в каскаде CSTR общее расчетное уравнение имеет вид ${\displaystyle C_{Ai}={\frac {-1+{\sqrt {1+4k_{i}\tau _{i}C_{A(i-1)}}}}{2k_{i}\tau _{i}}}}$

Неидеальный каскад CSTR

В случае неидеальных реакторов можно рассчитать распределение времени пребывания . При концентрации в j-м реакторе в серии определяется как

${\displaystyle {\frac {C_{j}}{C_{o}}}=1-e^{-{\frac {nt}{\bar {t}}}}[1+{\frac {nt}{\bar {t}}}+{\frac {1}{2!}}({\frac {nt}{\bar {t}}})^{2}+...+{\frac {1}{(j-1)!}}({\frac {nt}{\bar {t}}})^{j-1}]}$

где n — общее количество последовательно соединенных CSTR, а — среднее время пребывания каскада, определяемое выражением , где Q — объемный расход . ${\displaystyle {\bar {t}}}$ ${\displaystyle {\bar {t}}={\frac {V}{Q}}}$

Исходя из этого, распределение кумулятивного времени пребывания (F(t)) можно рассчитать как

${\displaystyle F(t)={\frac {C_{n}}{C_{o}}}=1-e^{-{\frac {nt}{\bar {t}}}}[1+{\frac {nt}{\bar {t}}}+{\frac {1}{2!}}({\frac {nt}{\bar {t}}})^{2}+...+{\frac {1}{(n-1)!}}({\frac {nt}{\bar {t}}})^{n-1}]}$

При n → ∞ F(t) приближается к идеальному ответу PFR. Дисперсия, связанная с F(t) для импульсного стимула в каскаде CSTR, равна . ${\displaystyle \sigma _{t}^{2}={\frac {{\bar {t}}^{2}}{n}}}$

Расходы

Первоначально стоимость снижается с ростом числа CSTR по мере уменьшения объема, но по мере увеличения эксплуатационных расходов общая стоимость в конечном итоге начинает расти.

При определении стоимости серии CSTR необходимо учитывать капитальные и эксплуатационные расходы . Как показано выше, увеличение количества CSTR в серии приведет к уменьшению общего объема реактора. Поскольку стоимость масштабируется с объемом, капитальные затраты снижаются при увеличении количества CSTR. Наибольшее снижение стоимости и, следовательно, объема происходит между одним CSTR и двумя CSTR в серии. При рассмотрении эксплуатационных расходов эксплуатационные расходы масштабируются с количеством насосов и элементов управления, строительством, установкой и обслуживанием, которые сопровождают более крупные каскады. Поэтому с увеличением количества CSTR увеличиваются эксплуатационные расходы. Следовательно, существует минимальная стоимость, связанная с каскадом CSTR.

Реакции нулевого порядка

Из перестановки уравнения, данного для идентичных изотермических CSTR, работающих в реакции нулевого порядка: , объем каждого отдельного CSTR будет масштабироваться на . Поэтому общий объем реактора не зависит от количества CSTR для реакции нулевого порядка. Поэтому стоимость не является функцией количества реакторов для реакции нулевого порядка и не уменьшается с увеличением количества CSTR. ${\displaystyle \tau ={\frac {C_{Ao}-C_{Am}}{mk}}}$ ${\displaystyle {\frac {1}{m}}}$

Селективность параллельных реакций

При рассмотрении параллельных реакций использование каскада CSTR может обеспечить большую селективность для желаемого продукта.

Для заданной параллельной реакции и с константами и и уравнениями скорости и , соответственно, мы можем получить соотношение между ними, разделив на . Следовательно . В случае, когда и B является желаемым продуктом, каскад CSTR благоприятствует свежему вторичному питанию для того, чтобы максимизировать концентрацию . ${\displaystyle {\ce {A -> B}}}$ ${\displaystyle {\ce {A -> C}}}$ ${\displaystyle k_{1}}$ ${\displaystyle k_{2}}$ ${\displaystyle {\frac {d[{\ce {B}}]}{dt}}=k_{1}[{\ce {A}}]^{n_{1}}}$ ${\displaystyle {\frac {d[{\ce {C}}]}{dt}}=k_{2}[{\ce {A}}]^{n_{2}}}$ ${\displaystyle {\frac {d[{\ce {B}}]}{dt}}}$ ${\displaystyle {\frac {d[{\ce {C}}]}{dt}}}$ ${\displaystyle {\frac {d[{\ce {B}}]}{d[{\ce {C}}]}}={\frac {k_{1}}{k_{2}}}[{\ce {A}}]^{n_{1}-n_{2}}}$ ${\displaystyle n_{1}>n_{2}}$ ${\displaystyle {\ce {A}}}$ ${\displaystyle {\ce {A}}}$

Для параллельной реакции с двумя или более реагентами, такими как и с константами и и уравнениями скорости и , соответственно, мы можем получить соотношение между ними, разделив на . Следовательно . В случае, когда и и B является желаемым продуктом, каскад CSTR с входящим потоком высокой и является предпочтительным. В случае, когда и и B является желаемым продуктом, каскад CSTR с высокой концентрацией в исходном материале и небольшими вторичными потоками является предпочтительным. ^[9] ${\displaystyle {\ce {A + D -> B}}}$ ${\displaystyle {\ce {A + D -> C}}}$ ${\displaystyle k_{1}}$ ${\displaystyle k_{2}}$ ${\displaystyle {\frac {d[{\ce {B}}]}{dt}}=k_{1}[{\ce {A}}]^{n_{1}}[{\ce {D}}]^{m_{1}}}$ ${\displaystyle {\frac {d[{\ce {C}}]}{dt}}=k_{2}[{\ce {A}}]^{n_{2}}[{\ce {D}}]^{m_{1}2}}$ ${\displaystyle {\frac {d[{\ce {B}}]}{dt}}}$ ${\displaystyle {\frac {d[{\ce {C}}]}{dt}}}$ ${\displaystyle {\frac {d[{\ce {B}}]}{d[{\ce {C}}]}}={\frac {k_{1}}{k_{2}}}[{\ce {A}}]^{n_{1}-n_{2}}[{\ce {D}}]^{m_{1}-m_{2}}}$ ${\displaystyle n_{1}>n_{2}}$ ${\displaystyle m_{1}>m_{2}}$ ${\displaystyle {\ce {[A]}}}$ ${\displaystyle {\ce {[D]}}}$ ${\displaystyle n_{1}>n_{2}}$ ${\displaystyle m_{1}<m_{2}}$ ${\displaystyle {\ce {A}}}$ ${\displaystyle {\ce {D}}}$

Последовательные реакции, такие как также имеют селективность между и , но CSTR в целом обычно не выбираются, когда желаемый продукт является как обратное смешивание от CSTR благоприятствует . Обычно для этих реакций выбирают реактор периодического действия или PFR . ${\displaystyle {\ce {A -> B -> C}}}$ ${\displaystyle {\ce {B}}}$ ${\displaystyle {\ce {C}}}$ ${\displaystyle {\ce {B}}}$ ${\displaystyle {\ce {C}}}$

Приложения

CSTR облегчают быстрое разбавление реагентов посредством смешивания. Поэтому для реакций ненулевого порядка низкая концентрация реагента в реакторе означает, что CSTR будет менее эффективен при удалении реагента по сравнению с PFR с тем же временем пребывания. ^[3] Поэтому CSTR обычно больше, чем PFR, что может быть проблемой в приложениях, где пространство ограничено. Однако одним из дополнительных преимуществ разбавления в CSTR является способность нейтрализовать удары в системе. В отличие от PFR, производительность CSTR менее восприимчива к изменениям в составе втекающего потока, что делает его идеальным для различных промышленных приложений:

Анаэробные реакторы на очистных сооружениях Newtown Creek в Гринпойнте, Бруклин

Экологическая инженерия

• Процесс очистки сточных вод с использованием активированного ила ^[2]
• Системы очистки лагун для естественной очистки сточных вод ^[2]
• Анаэробные реакторы для стабилизации твердых биологических веществ сточных вод ^[10]
• Очистные водно-болотные угодья для сточных вод и ливневых стоков ^[11]

Химическая инженерия

• Петлевой реактор для производства фармацевтических препаратов ^[12]

• Ферментация ^[12]
• Производство биогаза

Смотрите также

• Реактор с ламинарным потоком
• Микрореактор
• Реактор с колебательными перегородками
• Модель реактора идеального вытеснения

Примечания

Ссылки

1. Schmidt, Lanny D. (1998). Инженерия химических реакций . Нью-Йорк: Oxford University Press. ISBN 0-19-510588-5.
2. Metcalf & Eddy (2013-09-03). Водоочистка: очистка и восстановление ресурсов . Tchobanoglous, George,, Stensel, H. David,, Tsuchihashi, Ryujiro,, Burton, Franklin L. (Franklin Louis), 1927-, Abu-Orf, Mohammad,, Bowden, Gregory (Пятое изд.). Нью-Йорк, штат Нью-Йорк. ISBN 978-0-07-340118-8. OCLC  858915999.{{cite book}}: CS1 maint: location missing publisher (link)
3. Бенджамин, Марк М. (2013-06-13). Инженерия качества воды: физико-химические процессы очистки . Лоулер, Десмонд Ф. Хобокен, Нью-Джерси. ISBN 978-1-118-63227-7. OCLC  856567226.{{cite book}}: CS1 maint: location missing publisher (link)
4. Болин, Берт; Роде, Хеннинг (январь 1973 г.). «Заметка о понятиях возрастного распределения и времени прохождения в природных водоемах». Теллус . 25 (1): 58–62. Бибкод : 1973Скажите...25...58Б. дои : 10.3402/tellusa.v25i1.9644 . ISSN  0040-2826.
5. Monsen, Nancy E.; Cloern, James E.; Lucas, Lisa V.; Monismith, Stephen G. (сентябрь 2002 г.). «Комментарий к использованию времени промывки, времени пребывания и возраста в качестве шкал времени переноса». Limnology and Oceanography . 47 (5): 1545–1553. Bibcode : 2002LimOc..47.1545M. doi : 10.4319/lo.2002.47.5.1545 . S2CID  11505988.
6. Дэвис, Марк Э. (2003). Основы химической реакционной инженерии . Дэвис, Роберт Дж. (Международный редактор). Бостон: McGraw-Hill. ISBN 978-1-62870-437-2. OCLC  880604539.
7. Стоукс, Р. Л.; Науман, Э. Брюс (1970). «Функции распределения времени пребывания для последовательно соединенных резервуаров с мешалкой». Канадский журнал химической инженерии . 48 (6): 723–725.
8. Хилл, Чарльз Г.; Рут, Тэтчер В. (2014). Введение в химическую инженерную кинетику и проектирование реакторов, второе издание . Хобокен, Нью-Джерси: Wiley. С. 241–253, 349–358. ISBN 9781118368251.
9. Левеншпиль, Октав (1998). Химическая реакционная инженерия, 3-е издание . Wiley. ISBN 978-0-471-25424-9.
10. Hurtado, FJ; Kaiser, AS; Zamora, B. (март 2015 г.). «Анализ динамики жидкости в реакторе с непрерывным перемешиванием для технической оптимизации сбраживания сточных вод». Water Research . 71 : 282–293. Bibcode : 2015WatRe..71..282H. doi : 10.1016/j.watres.2014.11.053. ISSN  0043-1354. PMID  25635665.
11. Кадлек, Роберт Х.; Уоллес, Скотт Д. (2009). Лечение водно-болотных угодий (второе изд.). Бока-Ратон, Флорида, США: CRC Press. п. 181. ИСБН 978-1-56670-526-4.
12. "Визуальная энциклопедия химической инженерии". encyclopedia.che.engin.umich.edu . Архивировано из оригинала 2013-12-14 . Получено 2020-04-30 .