Максимальная длина последовательности

Тип псевдослучайной двоичной последовательности

Последовательность максимальной длины ( ПМД ) — это тип псевдослучайной двоичной последовательности .

Они представляют собой последовательности битов, генерируемые с использованием регистров сдвига с максимальной линейной обратной связью , и называются так потому, что являются периодическими и воспроизводят каждую двоичную последовательность (кроме нулевого вектора), которая может быть представлена ​​регистрами сдвига (т. е. для регистров длины m они производят последовательность длиной 2 ^m  − 1). MLS также иногда называют n-последовательностью или m-последовательностью . MLS являются спектрально плоскими , за исключением почти нулевого члена DC.

Эти последовательности могут быть представлены как коэффициенты неприводимых многочленов в кольце многочленов над Z/2Z .

Практические приложения для MLS включают измерение импульсных откликов (например, реверберации помещения или времени прибытия от буксируемых источников в океане ^[1] ). Они также используются в качестве основы для получения псевдослучайных последовательностей в цифровых системах связи, которые используют системы передачи с расширенным спектром прямой последовательности и скачкообразной перестройкой частоты , а также в эффективном проектировании некоторых экспериментов фМРТ . ^[2]

Поколение

Рисунок 1: Следующее значение регистра a ₃ в регистре сдвига с обратной связью длиной 4 определяется суммой по модулю 2 a ₀ и a ₁ .

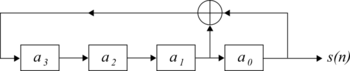
MLS генерируются с использованием регистров сдвига с максимальной линейной обратной связью . Система генерации MLS с регистром сдвига длиной 4 показана на рис. 1. Ее можно выразить с помощью следующего рекурсивного соотношения:

${\displaystyle {\begin{cases}a_{3}[n+1]=a_{0}[n]+a_{1}[n]\\a_{2}[n+1]=a_{3}[n]\\a_{1}[n+1]=a_{2}[n]\\a_{0}[n+1]=a_{1}[n]\\\end{cases}}}$

где n — это индекс времени, представляющий собой сложение по модулю 2. Для значений бит 0 = ЛОЖЬ или 1 = ИСТИНА это эквивалентно операции XOR. ${\displaystyle +}$

Поскольку MLS являются периодическими, а регистры сдвига циклически проходят через все возможные двоичные значения (за исключением нулевого вектора), регистры можно инициализировать в любом состоянии, за исключением нулевого вектора.

Полиномиальная интерпретация

Полином над GF(2) может быть связан с регистром сдвига с линейной обратной связью. Он имеет степень длины регистра сдвига и имеет коэффициенты, которые равны 0 или 1, что соответствует отводам регистра, которые питают вентиль xor . Например, полином, соответствующий рисунку 1, равен . ${\displaystyle x^{4}+x+1}$

Необходимым и достаточным условием для того, чтобы последовательность, сгенерированная LFSR, имела максимальную длину, является то, чтобы ее соответствующий полином был примитивным . ^[3]

Выполнение

MLS недороги в реализации на аппаратном или программном уровне, а регистры сдвига с обратной связью относительно низкого порядка могут генерировать длинные последовательности; последовательность, сгенерированная с использованием регистра сдвига длиной 20, имеет длину 2 ²⁰  − 1 выборок (1 048 575 выборок).

Свойства последовательностей максимальной длины

MLS обладают следующими свойствами, сформулированными Соломоном Голомбом . ^[4]

Остаток имущества

В последовательности должно быть примерно одинаковое количество 0 и 1. Точнее, в последовательности максимальной длины длины есть единицы и нули. Количество единиц равно количеству нулей плюс один, так как состояние, содержащее только нули, не может возникнуть. ${\displaystyle 2^{n}-1}$ ${\displaystyle 2^{n-1}}$ ${\displaystyle 2^{n-1}-1}$

Управлять собственностью

«Run» — это подпоследовательность последовательных «1» или последовательных «0» в пределах соответствующей MLS. Количество run — это количество таких подпоследовательностей. ^{[ неопределенно ]}

Из всех «серий» (состоящих из «1» или «0») в последовательности:

• Половина трасс имеет длину 1.
• Четверть трасс имеют длину 2.
• Одна восьмая часть трасс имеет длину 3.
• ... и т. д. ...

Корреляционное свойство

Круговая автокорреляция MLS представляет собой дельта -функцию Кронекера ^{[5] [6]} (со смещением постоянного тока и задержкой по времени, в зависимости от реализации). Для соглашения ±1, т. е. присваивается значение бита 1 и значение бита 0 , отображая XOR на отрицательное значение произведения: ${\displaystyle s=+1}$ ${\displaystyle s=-1}$

${\displaystyle R(n)={\frac {1}{N}}\sum _{m=1}^{N}s[m]\,s^{*}[m+n]_{N}={\begin{cases}1&{\text{if }}n=0,\\-{\frac {1}{N}}&{\text{if }}0<n<N.\end{cases}}}$

где представляет собой комплексно-сопряженное число, а представляет собой циклический сдвиг . ${\displaystyle s^{*}}$ ${\displaystyle [m+n]_{N}}$

Линейная автокорреляция MLS аппроксимирует дельту Кронекера.

Извлечение импульсных откликов

Если импульсный отклик линейной инвариантной во времени (LTI) системы должен быть измерен с помощью MLS, отклик может быть извлечен из измеренного выхода системы y [ n ], взяв его круговую взаимную корреляцию с MLS. Это происходит потому, что автокорреляция MLS равна 1 для нулевого запаздывания и почти равна нулю (−1/ N , где N — длина последовательности) для всех других запаздываний; другими словами, можно сказать, что автокорреляция MLS приближается к единичной импульсной функции по мере увеличения длины MLS.

Если импульсная характеристика системы равна h [ n ], а MLS равна s [ n ], то

${\displaystyle y[n]=(h*s)[n].\,}$

Принимая во внимание взаимную корреляцию относительно s [ n ] обеих сторон,

${\displaystyle {\phi }_{sy}=h[n]*{\phi }_{ss}\,}$

и предполагая, что φ _ss является импульсом (справедливо для длинных последовательностей)

${\displaystyle h[n]={\phi }_{sy}.\,}$

Любой сигнал с импульсной автокорреляцией может быть использован для этой цели, но сигналы с высоким крест-фактором , такие как сам импульс, производят импульсные отклики с плохим отношением сигнал/шум . Обычно предполагается, что MLS тогда будет идеальным сигналом, так как он состоит только из полномасштабных значений, а его цифровой крест-фактор равен минимуму, 0 дБ. ^{[7] [8]} Однако после аналоговой реконструкции резкие разрывы в сигнале производят сильные межвыборочные пики, ухудшая крест-фактор на 4-8 дБ или более, увеличиваясь с длиной сигнала, делая его хуже, чем синусоидальная развертка. ^[9] Другие сигналы были разработаны с минимальным крест-фактором, хотя неизвестно, можно ли его улучшить более чем на 3 дБ. ^[10]

Связь с преобразованием Адамара

Кон и Лемпель ^[11] показали связь MLS с преобразованием Адамара . Эта связь позволяет вычислять корреляцию MLS в быстром алгоритме, похожем на FFT .

Смотрите также

• Код Баркера
• Дополнительные последовательности
• Федеральный стандарт 1037C
• Частотная характеристика
• Золотой код
• Импульсный ответ
• Кольцо полиномов

Ссылки

• Голомб, Соломон В.; Гуан Гун (2005). Проектирование сигналов для хорошей корреляции: для беспроводной связи, криптографии и радаров. Cambridge University Press . ISBN 978-0-521-82104-9.

1. Gemba, Kay L.; Vazquez, Heriberto J.; Fialkowski, Joseph; Edelmann, Geoffrey F.; Dzieciuch, Matthew A.; Hodgkiss, William S. (октябрь 2021 г.). «Сравнение производительности m-последовательностей и линейных частотно-модулированных разверток для оценки времени прохождения с движущимся источником». Журнал акустического общества Америки . 150 (4): 2613–2623. Bibcode : 2021ASAJ..150.2613G. doi : 10.1121/10.0006656. PMID  34717519. S2CID  240355915.
2. Buracas GT, Boynton GM (июль 2002 г.). «Эффективный дизайн событийно-связанных экспериментов фМРТ с использованием М-последовательностей». NeuroImage . 16 (3 Pt 1): 801–13. doi :10.1006/nimg.2002.1116. PMID  12169264. S2CID  7433120.
3. «Линейные регистры сдвига с обратной связью — реализация, свойства M-последовательности, таблицы обратной связи»[1], New Wave Instruments (NW), дата обращения 03.12.2013.
4. Голомб, Соломон В. (1967). Последовательности сдвиговых регистров. Holden-Day. ISBN 0-89412-048-4.
5. Якобсен, Финн; Юль, Питер Моллер (2013-06-04). Основы общей линейной акустики. John Wiley & Sons. ISBN 978-1118636176Последовательность максимальной длины — это двоичная последовательность, круговая автокорреляция которой (за исключением небольшой ошибки постоянного тока) является дельта-функцией .
6. Sarwate, DV; Pursley, MB (1980-05-01). «Свойства кросскорреляции псевдослучайных и связанных последовательностей». Труды IEEE . 68 (5): 593–619. doi :10.1109/PROC.1980.11697. ISSN  0018-9219. S2CID  6179951.
7. "Маленькое руководство по MLS (последовательности максимальной длины) | dspGuru.com". dspguru.com . Получено 19.05.2016 . его среднеквадратичное и пиковое значения равны X, что делает его пик-фактор (пик/среднеквадратичное значение) равным 1, самому низкому значению, которое он может получить.
8. "Другие электроакустические измерительные методы". www.clear.rice.edu . Получено 2016-05-19 . Пик-фактор для MLS очень близок к 1, поэтому имеет смысл использовать этот тип входного сигнала, когда нам нужно высокое отношение сигнал/шум для нашего измерения
9. Чан, Иэн Х. "Swept Sine Chirps for Measuring Impulse Response" (PDF) . thinksrs.com . Получено 19.05.2016 . Последовательность максимальной длины (MLS) теоретически подходит, поскольку имеет математический пик-фактор 0 дБ, самый низкий возможный пик-фактор. Однако на практике резкие переходы и воспроизведение сигнала с ограниченной полосой пропускания приводят к пик-фактору около 8 дБ
10. Фризе, М. (1997-10-01). «Многотональные сигналы с низким коэффициентом амплитуды» (PDF) . IEEE Transactions on Communications . 45 (10): 1338–1344. doi :10.1109/26.634697. ISSN  0090-6778.
11. Кон, М.; Лемпель, А. (январь 1977 г.). «О быстрых преобразованиях М-последовательности». IEEE Trans. Inf. Theory . 23 (1): 135–7. doi :10.1109/TIT.1977.1055666.

Внешние ссылки

• Бристоу-Джонсон, Роберт. «Небольшой учебник MLS».— Краткое онлайн-руководство, описывающее, как MLS используется для получения импульсного отклика линейной стационарной системы . Также описывает, как нелинейности в системе могут проявляться в виде ложных всплесков в кажущемся импульсном отклике.
• Хи, Йенс. «Измерение импульсного отклика с использованием MLS» (PDF) . — Статья, описывающая генерацию MLS. Содержит C-код для генерации MLS с использованием до 18-отводных LFSR и соответствующего преобразования Адамара для извлечения импульсной характеристики.
• Шефер, Магнус (октябрь 2012 г.). «База данных импульсных реакций Ахена». Институт систем связи и обработки данных, Рейнско-Вестфальский технический университет Ахена. V1.4.База данных импульсных характеристик помещения (бинауральная), созданная с помощью последовательностей максимальной длины.
• «Эффективные сдвиговые регистры, счетчики LFSR и генераторы длинных псевдослучайных последовательностей — устаревшие» (PDF) . Xilinx. Июль 1996 г. XAPP052 v1.1.— Реализация lfsr в FPGA включает в себя список ответвлений для 3–168 бит