В археологии , сериация является относительным методом датирования , при котором комплексы или артефакты из многочисленных мест в одной культуре размещаются в хронологическом порядке. Там, где методы абсолютного датирования , такие как радиоуглеродный, не могут быть применены, археологам приходится использовать методы относительного датирования для датирования археологических находок и объектов. Сериация является стандартным методом датирования в археологии. Его можно использовать для датирования каменных орудий, фрагментов керамики и других артефактов. В Европе он часто использовался для реконструкции хронологической последовательности могил на кладбище (например, Jørgensen 1992; [1] Müssemeier, Nieveler et al. 2003). [2]
Применялись два различных варианта сериации: контекстная сериация и частотная сериация (Renfrew and Bahn 1996, стр. 116–117). В то время как контекстная сериация основана на наличии или отсутствии стиля дизайна , частотная сериация опирается на измерение пропорционального обилия или частоты стиля дизайна. Контекстная сериация часто используется для реконструкции хронологической последовательности захоронений, поскольку важно только наличие или отсутствие стиля или типа дизайна. Частотная сериация применяется в случаях большого количества объектов, принадлежащих к одному стилю. Примером этого являются собрания керамических черепков, которые включают примерно один и тот же диапазон типов, хотя и в разных пропорциях.
Флиндерс Петри проводил раскопки в Диосполисе Парва в Египте в конце девятнадцатого века. Он обнаружил, что могилы, которые он раскопал, не содержали никаких доказательств их датировки, а их дискретный характер означал, что последовательность не могла быть построена по их стратиграфии . Петри перечислил содержимое каждой могилы на полоске картона и менял листы местами, пока не пришел к последовательности, которая его удовлетворила. [3] Он рассуждал, что наиболее точной последовательностью будет та, где концентрации определенных стилей дизайна имели самую короткую продолжительность по последовательности листов (Renfrew and Bahn 1996, стр. 116; Kendall 1971, стр. 215; Shennan 1997, стр. 341 [4] ). В то время как Петри считается изобретателем контекстуальной сериализации, Брейнерд (1951) [5] и Робинсон (1951) [6] были первыми, кто обратился к проблеме частотной сериализации (Шеннан 1997, стр. 342 [4] ).
Предположение, что стили дизайна следуют кривой колокола популярности – медленно стартуя, достигая пика и затем угасая, когда другой стиль становится популярным – дает основу для частотной сериализации. Оно также предполагает, что популярность дизайна будет в целом схожей от сайта к сайту в пределах одной культуры . Кроме того, жизненно важно, чтобы продолжительность жизни различных стилей дизайна перекрывалась. Следуя этим правилам, совокупность объектов может быть размещена в последовательности, так что сайты с наиболее схожими пропорциями определенных стилей всегда будут вместе (Lock 2003, стр. 125).
Задача идентификации стилей дизайна, т. е. формирования групп объектов, принадлежащих к одному стилю дизайна, отнюдь не тривиальна. Создание типологии часто является основой для сериализации. Ошибки в типологии приводят к ошибкам в сериализации: например, если определенный стиль дизайна имел два пика популярности ( бимодальное распределение ), этот стиль дизайна не подходит для сериализации, и его включение в анализ может привести к странным результатам. Некоторые стили дизайна использовались в течение очень долгого времени, поскольку созданная форма была удобной, и не было добавлено никаких улучшений или украшений. Конечно, эти стили дизайна не подходят для хронологической сериализации. Например, говорят, что ножи раннего средневековья в Европе не показывают хронологических изменений.
В дополнение к временной организации, результаты сериализации могут отражать различия в сборке по социальному статусу, возрасту, полу или различия, возникающие из-за региональных различий (или комбинации двух или более из этих факторов). Шеннан (1997, стр. 343) [4] представляет результат сериализации датских кладов на основе типов артефактов, таких как кинжалы, топоры и мечи. Результат не является хронологической последовательностью из-за выбора типов, порядок, по-видимому, начинается с исключительно мужских кладов и заканчивается исключительно женскими.
Доран и Ходсон (1975, стр. 269) [7] перечисляют три условия, которые должны быть выполнены для получения результата хронологической сериализации:
В настоящее время результаты сериализации больше не производятся вручную, как во времена Петри, а с помощью соответствующих алгоритмов. Хотя, по словам Дэвида Джорджа Кендалла (1971), статья Петри уже показала глубокое понимание математики проблемы сериализации (Цитата: «...по моему мнению, Петри следует поставить в один ряд с величайшими прикладными математиками девятнадцатого века»). В списке Бакстера (2003, стр. 8) вех статистики в археологии статья Робинсона (1951) [6] является первой записью. Робинсон основал свой метод частотной сериализации на матрице подобия . В 1971 году Кендалл предложил использовать методы многомерного шкалирования для задач сериализации, и этот подход также использовался некоторыми другими учеными (см. Бакстер 2003, стр. 202–203). Бакстер также представляет обзор статистических методов для сериализации и описание этих подходов (стр. 202–207). В 1975 году Доран и Ходсон (стр. 269–281) [7] подробно обобщили современное состояние методов сериализации, дав подробные описания подходов Кендалла и Робинсона.
Сегодня наиболее популярный метод сериализации как для контекстных, так и для частотных задач основан на анализе соответствий . Последовательность первой оси анализа соответствий считается наилучшим порядком сериализации (Shennan 1997, [4] стр. 342; Lock 2003, стр. 127; Jensen & Høilund Nielsen 1997). Используя этот метод, устанавливается не только последовательность объектов, но и последовательность стилей дизайна. Обратите внимание, что для установления направления вычисленной последовательности необходимы внешние доказательства, т. е. метод не сообщает, является ли первый объект в последовательности самым старым или самым молодым объектом.
Кендалл (1971) применил многомерное масштабирование к данным кладбища Мюнзингена. Полученная диаграмма рассеяния имела форму подковы, где могилы были расположены на кривой в соответствии с их хронологическим порядком. Аналогичным образом, отображение оценок компонентов для первых двух осей результата анализа соответствия покажет параболу , если рассматриваемые стили дизайна контролируются только одним фактором (например, хронологией). Это называется эффектом арки Хиллом и Гаухом (1980). [8] И Кендалл, и Йенсен и Хойлунд Нильсен (1997) создали искусственные наборы данных, чтобы показать, что парабола приводит к идеальным обстоятельствам. Поэтому рекомендуется проверить диаграмму рассеяния первых двух осей анализа соответствия, чтобы выяснить, играют ли роль и другие факторы (см. Примеры 2 и 3).
Если важен более одного фактора, эффект арки может исказить результаты. Хилл и Гаух (1980) представили метод устранения этого эффекта.
В 2003 году Гроенен и Побломе адаптировали алгоритм анализа соответствий, чтобы объединить сериализацию с абсолютными датами и стратиграфическими отношениями. [9] [10]
Небольшой пример ниже был вдохновлен последовательной классификацией египетской керамики Флиндерса Питри, опубликованной Ренфрю и Баном (1996, стр. 117).



Необработанные данные хранятся в несортированной двоичной таблице сопряженности , указывающей, какой стиль дизайна можно найти в каком контексте с помощью символа звезды. Например, рассмотрим первый столбец: контекст 3 содержит стили дизайна blackrim , bottle и handle . Стакан содержится в контекстах 1 и 2. Контекстная сериализация сортирует стили дизайна и контексты таким образом, что символы звезды находятся как можно ближе к диагонали таблицы. Конечно, для небольших примеров, таких как этот, не нужны никакие компьютерные программы, чтобы найти наилучший порядок, но для больших наборов данных, таких как 900 могил, изученных Петри, они чрезвычайно полезны.
Данные, представленные в этом примере, были смоделированы WinBasp. Первоначально было создано 60 контекстов (называемых единицами в WinBasp) вместе с 50 типами. Контексты были помечены в хронологическом порядке числами от 01 до 60, типы помечены в форме T00001 до T00050. Если тип представлен только одним объектом, этот объект не имеет значения для хронологической последовательности, поскольку он не обеспечивает ссылку на другой контекст. Аналогично, контексты, содержащие только один объект, не имеют значения для сериализации. Поэтому контексты с одним или без объекта и типы, представленные одним объектом или не представленные вообще, были исключены. Полученные необработанные смоделированные данные, состоящие из 43 контекстов и 34 типов, показаны слева. Как и ожидалось, точки, указывающие на вхождение типа в контекст, находятся близко к диагонали таблицы.


Изображение справа показывает результат сериализации для этого набора данных. Обратите внимание, что точки еще более компактны по диагонали таблицы по сравнению с необработанными данными. Это показывает небольшую проблему сериализации: на самом деле интервалы производства могут быть несколько длиннее, чем рассчитанные алгоритмом. В целом, последовательности контекстов и типов, рассчитанные алгоритмом сериализации, не являются правильными хронологическими последовательностями, но они довольно близки.

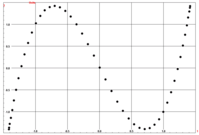
На изображении выше показана диаграмма рассеяния с типичной формой параболы первых двух осей анализа соответствия для контекстов смоделированного набора данных.

Таблица сопряженности показывает 29 контекстов с идеальными данными сериализации, созданными Кендаллом и Йенсеном и Хёйлундом Нильсеном (см. выше). С каждым новым контекстом появляется новый тип, а другой исчезает. Для этих регулярных данных кажется разумным предположить постоянные временные интервалы для контекстов, смежных во времени.
Результаты анализа соответствий, показанные на рисунках ниже, были рассчитаны на основе 49 контекстов с идеальными данными сериализации. Диаграмма рассеяния первых двух осей анализа соответствий показывает типичную форму параболы. Отображение оценок на первой и третьей осях показывает точки, лежащие на кривой полинома третьей степени . Аналогично, график оценок на первой и четвертой осях покажет полином четвертой степени для идеальных данных – и так далее.
Обратите внимание, что расстояния оценок для смежных контекстов на первой оси различаются: в начале и конце расстояния чрезвычайно малы, самые большие расстояния в центре примерно в 30 раз больше самых маленьких. Хилл и Гаух (1979) [8] создали похожую таблицу сопряженности с регулярной структурой, в которой каждый контекст содержит шесть типов. Они также отмечают, что расстояния внутри контекста меньше на концах, чем в середине. Это было одной из причин, по которой они предложили корректировку, которая называется детрендированным анализом соответствий .
Тем не менее, некоторые археологи считают, что линейное преобразование оценок на первой оси на основе некоторых известных абсолютных дат создаст хорошие оценки для неизвестных абсолютных дат, и этот подход является основой метода, представленного Гроененом и Побломе (см. выше), для объединения относительных и абсолютных дат. Этот идеальный пример показывает, что линейное преобразование может быть неподходящим во всех случаях, хотя исследование моделирования, проведенное ван де Вельденом, Гроененом и Побломе, приходит к выводу, что прогнозы подхода довольно хороши. [11]

Археологическая последовательность (или сокращенно последовательность) на конкретном археологическом объекте может быть определена на двух уровнях строгости.
{{cite web}}: CS1 maint: архивная копия как заголовок ( ссылка )ван де Вельден, М., Гроенен, П.Дж.Ф., Поблом, Дж. (2007). Сериация с помощью анализа ограниченного соответствия: исследование моделирования. Отчет Эконометрического института EI 2007-40.