

Соленоид ( / ˈ s oʊ l ə n ɔɪ d / [ 1] ) — тип электромагнита, образованного спиральной катушкой провода , длина которой существенно больше ее диаметра, [2] который генерирует контролируемое магнитное поле . Катушка может создавать однородное магнитное поле в объеме пространства, когда через нее проходит электрический ток .
Андре-Мари Ампер ввел термин «соленоид» в 1823 году, придумав само устройство в 1820 году. [3] Французский термин, первоначально созданный Ампером, — solénoïde , который является французской транслитерацией греческого слова σωληνοειδὴς , что означает трубчатый .
Винтовая катушка соленоида не обязательно должна вращаться вокруг прямолинейной оси; например, электромагнит Уильяма Стерджена 1824 года состоял из соленоида, изогнутого в форме подковы (подобно дуговой пружине ).
Соленоиды обеспечивают магнитную фокусировку электронов в вакууме, особенно в телевизионных камерах, таких как видиконы и ортиконы изображения. Электроны движутся по спиральным траекториям в магнитном поле. Эти соленоиды, фокусирующие катушки, окружают почти всю длину трубки.

Бесконечный соленоид имеет бесконечную длину, но конечный диаметр. «Непрерывный» означает, что соленоид образован не дискретными катушками конечной ширины, а множеством бесконечно тонких катушек без пространства между ними; в этой абстракции соленоид часто рассматривается как цилиндрический лист проводящего материала.
Магнитное поле внутри бесконечно длинного соленоида однородно, и его напряженность не зависит ни от расстояния до оси, ни от площади поперечного сечения соленоида.
Это вывод плотности магнитного потока вокруг соленоида, который достаточно длинный, чтобы можно было игнорировать краевые эффекты. На рисунке 1 мы сразу знаем, что вектор плотности потока указывает в положительном направлении z внутри соленоида и в отрицательном направлении z снаружи соленоида. Мы подтверждаем это, применяя правило правой руки для поля вокруг провода. Если мы обхватим провод правой рукой, указав большим пальцем в направлении тока, изгиб пальцев покажет, как ведет себя поле. Поскольку мы имеем дело с длинным соленоидом, все компоненты магнитного поля, не направленные вверх, компенсируются симметрией. Снаружи происходит аналогичное погашение, и поле направлено только вниз.
Теперь рассмотрим воображаемую петлю c, которая находится внутри соленоида. По закону Ампера мы знаем, что линейный интеграл B (вектора плотности магнитного потока) вокруг этой петли равен нулю, поскольку она не охватывает никаких электрических токов (можно также предположить, что электрическое поле контура, проходящее через петлю, является постоянным при таких условиях: постоянный или постоянно изменяющийся ток через соленоид). Выше мы показали, что поле направлено вверх внутри соленоида, поэтому горизонтальные части петли c не вносят никакого вклада в интеграл. Таким образом, интеграл верхней стороны 1 равен интегралу нижней стороны 2. Поскольку мы можем произвольно изменять размеры петли и получать тот же результат, единственным физическим объяснением является то, что подынтегральные выражения фактически равны, то есть магнитное поле внутри соленоида является радиально однородным. Однако следует отметить, что ничто не запрещает ему изменяться в продольном направлении, что на самом деле и происходит.
Аналогичный аргумент можно применить к петле a, чтобы сделать вывод, что поле снаружи соленоида является радиально однородным или постоянным. Этот последний результат, который строго верен только вблизи центра соленоида, где линии поля параллельны его длине, важен, поскольку он показывает, что плотность потока снаружи практически равна нулю, поскольку радиусы поля снаружи соленоида будут стремиться к бесконечности. Интуитивный аргумент также можно использовать, чтобы показать, что плотность потока снаружи соленоида фактически равна нулю. Линии магнитного поля существуют только в виде петель, они не могут расходиться или сходиться в точке, как это могут делать линии электрического поля (см. закон Гаусса для магнетизма ). Линии магнитного поля следуют продольному пути соленоида внутри, поэтому они должны идти в противоположном направлении снаружи соленоида, чтобы линии могли образовывать петли. Однако объем снаружи соленоида намного больше объема внутри, поэтому плотность линий магнитного поля снаружи значительно уменьшается. Теперь вспомним, что поле снаружи постоянно. Для того чтобы общее число линий поля сохранялось, внешнее поле должно стремиться к нулю по мере удлинения соленоида. Конечно, если соленоид сконструирован как проволочная спираль (как часто делается на практике), то он излучает внешнее поле так же, как и одиночный провод, из-за тока, текущего по всей длине соленоида.
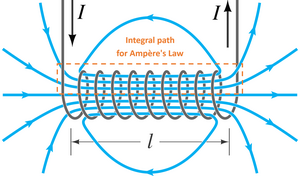
Применив закон Ампера к соленоиду (см. рисунок справа), мы получаем
где - плотность магнитного потока , - длина соленоида, - магнитная постоянная , - число витков, - ток. Отсюда получаем
Это уравнение справедливо для соленоида в свободном пространстве, что означает, что проницаемость магнитного пути такая же, как проницаемость свободного пространства, μ 0 .
Если соленоид погрузить в материал с относительной проницаемостью μ r , то поле увеличится на эту величину:
В большинстве соленоидов соленоид не погружен в материал с более высокой проницаемостью, а некоторая часть пространства вокруг соленоида имеет материал с более высокой проницаемостью, а часть представляет собой просто воздух (который ведет себя во многом как свободное пространство). В этом сценарии полный эффект материала с высокой проницаемостью не виден, но будет эффективная (или кажущаяся) проницаемость μ eff такая, что 1 ≤ μ eff ≤ μ r .
Включение ферромагнитного сердечника, например, железа , увеличивает величину магнитной индукции в соленоиде и повышает эффективную проницаемость магнитного пути. Это выражается формулой
где μ eff — эффективная или кажущаяся проницаемость сердечника. Эффективная проницаемость является функцией геометрических свойств сердечника и его относительной проницаемости. Термины относительная проницаемость (свойство только материала) и эффективная проницаемость (свойство всей структуры) часто путают; они могут отличаться на много порядков величины.
Для открытой магнитной структуры соотношение между эффективной проницаемостью и относительной проницаемостью определяется следующим образом:
где k — коэффициент размагничивания сердечника. [4]
Конечный соленоид — это соленоид с конечной длиной. Непрерывный означает, что соленоид образован не дискретными катушками, а листом проводящего материала. Мы предполагаем, что ток равномерно распределен по поверхности соленоида с поверхностной плотностью тока K ; в цилиндрических координатах :
Магнитное поле можно найти с помощью векторного потенциала , который для конечного соленоида радиусом R и длиной l в цилиндрических координатах равен [5] [6]

Где:
Здесь , и — полные эллиптические интегралы первого, второго и третьего рода.
С использованием:
Плотность магнитного потока получается как [7] [8] [9]
На оси симметрии радиальная составляющая обращается в нуль, а аксиальная составляющая поля равна Внутри соленоида, вдали от концов ( ), она стремится к постоянному значению .
Для случая, когда радиус намного больше длины соленоида ( ), плотность магнитного потока через центр соленоида (в направлении z , параллельном длине соленоида, где катушка центрирована при z = 0) можно оценить как плотность потока одного круглого проводящего контура:

В категории конечных соленоидов есть те, которые имеют редкую намотку с одним шагом, те, которые имеют редкую намотку с переменным шагом (соленоид с переменным шагом), и те, которые имеют переменные радиусы для разных петель (нецилиндрические соленоиды). Их называют нерегулярными соленоидами . Они нашли применение в различных областях, таких как редко намотанные соленоиды для беспроводной передачи энергии , [10] [11] соленоиды с переменным шагом для магнитно-резонансной томографии (МРТ), [12] и нецилиндрические соленоиды для других медицинских устройств. [13]
Расчет собственной индуктивности и емкости не может быть выполнен с использованием тех, которые используются для обычных соленоидов, т.е. плотно намотанными. Были предложены новые методы расчета для расчета собственной индуктивности [14] (коды доступны в [15] ) и емкости. [16] (коды доступны в [17] )
Как показано выше, плотность магнитного потока внутри катушки практически постоянна и определяется выражением
где μ 0 - магнитная постоянная , число витков, ток и длина катушки. Игнорируя концевые эффекты, полный магнитный поток через катушку получается путем умножения плотности потока на площадь поперечного сечения :
Объединяя это с определением индуктивности
индуктивность соленоида вычисляется как
Таблица индуктивности для коротких соленоидов с различными отношениями диаметра к длине была рассчитана Деллингером, Уиттмором и Улдом. [18]
Эту и индуктивность более сложных форм можно вывести из уравнений Максвелла . Для жестких катушек с воздушным сердечником индуктивность является функцией геометрии катушки и числа витков и не зависит от тока.
Аналогичный анализ применим к соленоиду с магнитным сердечником, но только если длина катушки намного больше, чем произведение относительной проницаемости магнитного сердечника и диаметра. Это ограничивает простой анализ сердечниками с низкой проницаемостью или чрезвычайно длинными тонкими соленоидами. Наличие сердечника можно учесть в приведенных выше уравнениях, заменив магнитную постоянную μ 0 на μ или μ 0 μ r , где μ представляет проницаемость, а μ r относительную проницаемость . Обратите внимание, что поскольку проницаемость ферромагнитных материалов изменяется с приложенным магнитным потоком, индуктивность катушки с ферромагнитным сердечником, как правило, будет изменяться с током.
{{cite web}}: CS1 maint: archived copy as title (link){{cite web}}: CS1 maint: archived copy as title (link){{cite journal}}: Цитировать журнал требует |journal=( помощь ){{cite journal}}: Цитировать журнал требует |journal=( помощь ){{cite book}}: |journal=проигнорировано ( помощь )