Метод согласованных асимптотических разложений

В математике метод согласованных асимптотических разложений ^[1] является распространенным подходом к поиску точного приближения к решению уравнения или системы уравнений . Он особенно используется при решении сингулярно возмущенных дифференциальных уравнений . Он включает в себя нахождение нескольких различных приближенных решений, каждое из которых является действительным (т.е. точным) для части диапазона независимой переменной, а затем объединение этих различных решений вместе, чтобы дать одно приближенное решение, действительное для всего диапазона значений независимой переменной. независимая переменная. В отечественной литературе эти методы были известны под названием «промежуточной асимптотики» и были введены в работах Якова Зельдовича и Григория Баренблатта .

Обзор метода

В большом классе сингулярно возмущенных задач область может быть разделена на две или более подобластей. В одном из них, часто самом большом, решение точно аппроксимируется асимптотическим рядом ^[2] , найденным путем рассмотрения проблемы как регулярного возмущения (т.е. путем установки нуля относительно небольшого параметра). Другие подобласти состоят из одной или нескольких небольших областей, в которых это приближение является неточным, обычно потому, что члены возмущения в задаче там не являются пренебрежимо малыми. Эти области в целом называются переходными слоями , а в частности — пограничными слоями или внутренними слоями в зависимости от того, расположены ли они на границе области (как это обычно бывает в приложениях) или внутри области соответственно.

Аппроксимация в виде асимптотического ряда получается в переходном слое(ях) путем рассмотрения этой части области как отдельной задачи возмущения. Это приближение называется внутренним решением , а другое — внешним решением , названным в честь их связи с переходным слоем(ями). Затем внешние и внутренние решения объединяются посредством процесса, называемого «сопоставлением», таким образом, что получается приближенное решение для всей области. ^{[3] [4] [5] [6]}

Простой пример

Рассмотрим краевую задачу

$${\displaystyle \varepsilon y''+(1+\varepsilon )y'+y=0,}$$

${\displaystyle y}$ ${\displaystyle t}$ ${\displaystyle y(0)=0}$ ${\displaystyle y(1)=1}$ ${\displaystyle \varepsilon }$ ${\displaystyle 0<\varepsilon \ll 1}$

Внешнее решение, справедливое для t  =  O (1)

Поскольку оно очень мало, наш первый подход состоит в том, чтобы рассматривать уравнение как регулярную задачу возмущения, т. е. выполнить аппроксимацию и, следовательно, найти решение проблемы ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon =0}$

$${\displaystyle y'+y=0.}$$

В качестве альтернативы, учтите, что когда и оба имеют размер O (1), четыре члена в левой части исходного уравнения имеют соответственно размеры , O (1) и O (1). Таким образом, баланс ведущего порядка на этой временной шкале, действительный в выделенном пределе , задается вторым и четвертым членами, т. е. ${\displaystyle y}$ ${\displaystyle t}$ ${\displaystyle O(\varepsilon )}$ ${\displaystyle O(\varepsilon )}$ ${\displaystyle \varepsilon \to 0}$ ${\displaystyle y'+y=0.}$

Это имеет решение

$${\displaystyle y=Ae^{-t}}$$

сингулярного возмущения ${\displaystyle A}$ ${\displaystyle y(0)=0}$ ${\displaystyle A=0}$ ${\displaystyle y(1)=1}$ ${\displaystyle A=e}$ ${\displaystyle \varepsilon =0}$ ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon }$ ${\displaystyle t}$ ${\displaystyle t}$ ${\displaystyle \varepsilon }$ ${\displaystyle t=0}$ ${\displaystyle y(1)=1}$ ${\displaystyle A=e}$ ${\displaystyle y_{\mathrm {O} }=e^{1-t}}$

Внутреннее решение, действительное для t  =  O ( ε )

Во внутренней области и оба крошечные, но сопоставимого размера, поэтому определите новую переменную времени O (1) . Измените масштаб исходной краевой задачи, заменив на , и проблема станет ${\displaystyle t}$ ${\displaystyle \varepsilon }$ ${\displaystyle \tau =t/\varepsilon }$ ${\displaystyle t}$ ${\displaystyle \tau \varepsilon }$

$${\displaystyle {\frac {1}{\varepsilon }}y''(\tau )+\left({1+\varepsilon }\right){\frac {1}{\varepsilon }}y'(\tau )+y(\tau )=0,}$$

${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon =0}$

$${\displaystyle y''+y'=0.}$$

Альтернативно, учтите, что когда размер уменьшился до размера , то он по-прежнему имеет размер O (1) (используя выражение для ), и поэтому четыре члена в левой части исходного уравнения имеют соответственно размеры , , O (1) и О (1). Таким образом, баланс ведущего порядка в этой временной шкале, действительный в выделенном пределе , задается первым и вторым членами, т.е. ${\displaystyle t}$ ${\displaystyle O(\varepsilon )}$ ${\displaystyle y}$ ${\displaystyle y_{\mathrm {O} }}$ ${\displaystyle O(\varepsilon ^{-1})}$ ${\displaystyle O(\varepsilon ^{-1})}$ ${\displaystyle \varepsilon \to 0}$ ${\displaystyle y''+y'=0.}$

Это имеет решение

$${\displaystyle y=B-Ce^{-\tau }}$$

${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle y(0)=0}$ ${\displaystyle B=C}$

$${\displaystyle y_{\mathrm {I} }=B\left({1-e^{-\tau }}\right)=B\left({1-e^{-t/\varepsilon }}\right).}$$

Соответствие

Мы используем сопоставление, чтобы найти значение константы . Идея сопоставления состоит в том, что внутренние и внешние решения должны согласовываться для значений в промежуточной (или перекрывающейся) области, т.е. где . Нам нужно, чтобы внешний предел внутреннего решения соответствовал внутреннему пределу внешнего решения, т. е. ${\displaystyle B}$ ${\displaystyle t}$ ${\displaystyle \varepsilon \ll t\ll 1}$

$${\displaystyle \lim _{\tau \to \infty }y_{\mathrm {I} }=\lim _{t\to 0}y_{\mathrm {O} },}$$

${\displaystyle B=e}$

Описанная выше задача является простейшей из простых задач, касающихся согласованных асимптотических разложений. Можно сразу вычислить, что это весь асимптотический ряд для внешней области, тогда как поправка к внутреннему решению равна, а константа интегрирования должна быть получена из внутреннего и внешнего сопоставления. ${\displaystyle e^{1-t}}$ ${\displaystyle {\mathcal {O}}(\varepsilon )}$ ${\displaystyle y_{\mathrm {I} }}$ ${\textstyle B(1-e^{-t/\varepsilon })}$ ${\displaystyle B}$

Обратите внимание: интуитивная идея согласования пределов, т. е., не применима на этом уровне. Это просто потому, что подчеркнутый член не сходится к пределу. В таких случаях следует либо использовать а) метод промежуточной переменной, либо использовать б) правило соответствия Ван-Дайка. Первый метод громоздок и работает всегда, тогда как правило Ван-Дейка легко реализовать, но его применимость ограничена. Конкретная краевая задача, имеющая все необходимые компоненты, состоит в следующем. ${\textstyle \lim _{\tau \to \infty }y_{\mathrm {I} }=\lim _{t\to 0}y_{\mathrm {O} },}$

Рассмотрим краевую задачу

$${\displaystyle \varepsilon y''-x^{2}y'-y=1,\quad y(0)=y(1)=1}$$

Обычное внешнее разложение дает , где должно быть получено в результате сопоставления. ${\displaystyle y_{\mathrm {O} }=y_{0}+\varepsilon y_{1}+\cdots }$ ${\displaystyle y_{0}=\alpha e^{1/x}-1}$ ${\displaystyle \alpha }$

В задаче есть пограничные слои как слева, так и справа. Левый пограничный слой вблизи имеет толщину, тогда как правый пограничный слой вблизи имеет толщину . Давайте сначала вычислим решение в левом пограничном слое путем изменения масштаба , затем дифференциальное уравнение, которому нужно удовлетворять слева, будет ${\displaystyle 0}$ ${\displaystyle \varepsilon ^{1/2}}$ ${\displaystyle 1}$ ${\displaystyle \varepsilon }$ ${\displaystyle X=x/\varepsilon ^{1/2},\;Y=y}$

$${\displaystyle Y''-\varepsilon ^{1/2}X^{2}Y'-Y=1,\quad Y(0)=1}$$

${\displaystyle Y^{l}=Y_{0}^{l}+\varepsilon ^{1/2}Y_{1/2}^{l}+\cdots }$

Неоднородное состояние слева дает нам повод начать расширение с . Решением ведущего порядка является . ${\displaystyle {\mathcal {O}}(1)}$ ${\displaystyle {\mathcal {O}}(1)}$ ${\displaystyle Y_{0}^{l}=2e^{-X}-1}$

Это вместе с сопоставлением Ван-Дейка дает . ${\displaystyle 1-1}$ ${\displaystyle \alpha =0}$

Давайте теперь вычислим решение при правом масштабировании , тогда дифференциальное уравнение, которое должно удовлетворяться справа, будет ${\displaystyle X=(1-x)/\varepsilon ,\;Y=y}$

$${\displaystyle Y''+\left(1-2\varepsilon X+\varepsilon ^{2}X^{2}\right)Y'-\varepsilon Y=\varepsilon ,\quad Y(1)=1,}$$

$${\displaystyle Y^{r}=Y_{0}^{r}+\varepsilon Y_{1}^{r}+\cdots .}$$

Неоднородное состояние справа дает нам повод начать расширение с . Решением ведущего порядка является . Это с учетом сопоставления Ван-Дейка дает . Действуя аналогичным образом, если мы вычислим поправки более высокого порядка, мы получим решения как ${\displaystyle {\mathcal {O}}(1)}$ ${\displaystyle {\mathcal {O}}(1)}$ ${\displaystyle Y_{0}^{r}=(1-B)+Be^{-X}}$ ${\displaystyle 1-1}$ ${\displaystyle B=2}$

$${\displaystyle Y^{l}=2e^{-X}-1+\varepsilon ^{1/2}e^{-X}\left({\frac {X^{3}}{3}}+{\frac {X^{2}}{2}}+{\frac {X}{2}}\right)+{\mathcal {O}}(\varepsilon ),\quad X={\frac {x}{\varepsilon ^{1/2}}}.}$$

$${\displaystyle y\equiv -1.}$$

$${\displaystyle Y^{r}=2e^{-X}-1+2\varepsilon e^{-X}\left(X+X^{2}\right)+{\mathcal {O}}(\varepsilon ^{2}),\quad X={\frac {1-x}{\varepsilon }}.}$$

Композитное решение

Чтобы получить окончательное согласованное составное решение, действительное для всей области, одним из популярных методов является унифицированный метод. В этом методе мы добавляем внутреннюю и внешнюю аппроксимации и вычитаем их перекрывающееся значение , которое в противном случае учитывалось бы дважды. Значение перекрытия — это внешний предел решения внутреннего пограничного слоя и внутренний предел внешнего решения; выше установлено, что эти пределы равны . Следовательно, окончательное приближенное решение этой краевой задачи имеет вид: ${\displaystyle \,y_{\mathrm {overlap} }}$ ${\displaystyle e}$

$${\displaystyle y(t)=y_{\mathrm {I} }+y_{\mathrm {O} }-y_{\mathrm {overlap} }=e\left({1-e^{-t/\varepsilon }}\right)+e^{1-t}-e=e\left({e^{-t}-e^{-t/\varepsilon }}\right).}$$

Обратите внимание, что это выражение правильно сводится к выражениям для и когда is и O (1) соответственно. ${\displaystyle y_{\mathrm {I} }}$ ${\displaystyle y_{\mathrm {O} }}$ ${\displaystyle t}$ ${\displaystyle O(\varepsilon )}$

Точность

Сходимость приближений. Для различных значений показаны аппроксимации и точные решения, неразличимые в этом масштабе . Также показано внешнее решение. Заметим, что поскольку с уменьшением пограничный слой становится уже , то аппроксимации почти всюду сходятся к внешнему решению поточечно , но не равномерно . ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon }$

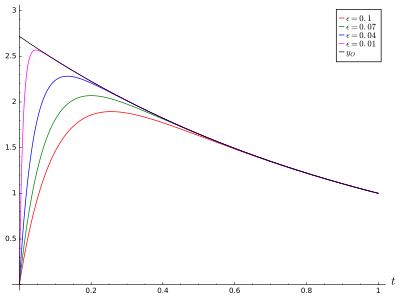
Это окончательное решение удовлетворяет исходному дифференциальному уравнению задачи (показанному путем подстановки его и его производных в исходное уравнение). Кроме того, граничные условия, полученные этим окончательным решением, соответствуют значениям, заданным в задаче, с точностью до постоянного кратного числа. Из-за единственности решения это означает, что согласованное асимптотическое решение идентично точному решению с точностью до постоянного кратного. Это не всегда так, любые оставшиеся члены должны стремиться к нулю равномерно при . ${\displaystyle \varepsilon \rightarrow 0}$

Наше решение не только успешно решает проблему, но и близко приближается к ее точному решению. Бывает, что эта конкретная задача легко находит точное решение.

$${\displaystyle y(t)={\frac {e^{-t}-e^{-t/\varepsilon }}{e^{-1}-e^{-1/\varepsilon }}},}$$

${\displaystyle e^{1-1/\varepsilon }}$

Расположение пограничного слоя

Удобно, что мы видим, что пограничный слой, где и большие, находится вблизи , как мы предполагали ранее. Если бы мы предположили, что он находится в другой конечной точке, и продолжили бы масштабирование , мы бы обнаружили, что невозможно удовлетворить полученное условие соответствия. Для многих задач такого рода метод проб и ошибок является единственным способом определить истинное местоположение пограничного слоя. ^[3] ${\displaystyle y'}$ ${\displaystyle y''}$ ${\displaystyle t=0}$ ${\displaystyle \tau =(1-t)/\varepsilon }$

Более сложные проблемы

Приведенная выше задача является простым примером, поскольку это одно уравнение только с одной зависимой переменной, и в решении имеется один пограничный слой. Более сложные задачи могут содержать несколько взаимозависимых переменных в системе нескольких уравнений и/или с несколькими граничными и/или внутренними слоями решения.

Часто желательно найти больше членов в асимптотических разложениях как внешнего, так и внутреннего решения. Соответствующая форма этих разложений не всегда ясна: хотя разложение в степенной ряд может работать, иногда подходящая форма включает дробные степени , такие функции, как , и так далее. Как и в приведенном выше примере, мы получим внешнее и внутреннее разложение с некоторыми коэффициентами, которые необходимо определить путем сопоставления. ^[7] ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon \log \varepsilon }$

Дифференциальные уравнения второго порядка

Дифференциальные уравнения второго порядка типа Шрёдингера

Метод согласованных асимптотических разложений - с сопоставлением решений в общей области применимости - был разработан и широко использовался Динглом и Мюллером-Кирстеном для получения асимптотических разложений решений и характеристических чисел (границ зон) шредингеровских уравнений. дифференциальные уравнения второго порядка с периодическими потенциалами - в частности, для уравнения Матье ^[8] (лучший пример), Ламе и эллипсоидальных волновых уравнений, ^[9] сплюснутых ^[10] и вытянутых ^[11] сфероидальных волновых уравнений и уравнений с ангармоническими потенциалами. . ^[12]

Уравнения конвекции-диффузии

Разработаны методы согласованных асимптотических разложений для поиска приближенных решений уравнения конвекции-диффузии Смолуховского , которое представляет собой сингулярно возмущенное дифференциальное уравнение второго порядка. Проблема изучалась, в частности, в контексте коллоидных частиц в линейных полях потока, где переменная задается парной функцией распределения вокруг пробной частицы. В пределе малого числа Пекле уравнение конвекции-диффузии также представляет сингулярность на бесконечном расстоянии (где обычно должно быть размещено граничное условие в дальней зоне ) из-за линейности поля потока при разделении между частицами. Эту проблему можно обойти с помощью пространственного преобразования Фурье, как показал Ян Донт. ^[13] Другой подход к решению этой задачи был разработан Алессио Закконе с соавторами и заключается в размещении граничного условия прямо на расстоянии пограничного слоя, при условии (в первом приближении) постоянного значения парной функции распределения в внешний слой из-за того, что там преобладает конвекция. Это приводит к приближенной теории скорости встречи двух взаимодействующих коллоидных частиц в линейном поле потока, которая хорошо согласуется с полным численным решением. ^[14] Когда число Пекле значительно больше единицы, сингулярность при бесконечном разделении больше не возникает и метод согласованной асимптотики может быть применен для построения полного решения для парной функции распределения во всей области. ^{[15] [16]}

Смотрите также

• Асимптотический анализ
• Многомасштабный анализ
• Асимптотика энергии активации

Рекомендации

1. О'Мэлли, Роберт Э. (2014), О'Мэлли, Роберт Э. (ред.), «Метод согласованных асимптотических разложений и его обобщения», Историческое развитие сингулярных возмущений , Cham: Springer International Publishing, стр. 53–121, номер домена : 10.1007/978-3-319-11924-3_3, ISBN 978-3-319-11924-3, получено 4 мая 2023 г.
2. Р.Б. Дингл (1973), Асимптотические разложения: их вывод и интерпретация , Academic Press .
3. Верхюльст, Ф. (2005). Методы и приложения сингулярных возмущений: пограничные слои и динамика множественных временных масштабов . Спрингер. ISBN 0-387-22966-3.
4. Найфе, АХ (2000). Методы возмущения . Библиотека классической литературы Уайли. Уайли-Интерсайенс. ISBN 978-0-471-39917-9.
5. Кеворкян, Дж.; Коул, доктор юридических наук (1996). Методы многомасштабных и сингулярных возмущений . Спрингер. ISBN 0-387-94202-5.
6. Бендер, СМ; Орзаг, С.А. (1999). Передовые математические методы для ученых и инженеров . Спрингер. ISBN 978-0-387-98931-0.
7. Хинч, Джон (1991). Методы возмущения . Издательство Кембриджского университета .
8. Р.Б. Дингл и Х.Дж.В. Мюллер, Дж. Рейн Ангью. Математика. 211 (1962) 11-32 и 216 (1964) 123-133; HJW Мюллер, Дж. Рейн Ангью. Математика. 211 (1962) 179-190.
9. HJW Müller, Mathematische Nachrichten 31 (1966) 89-101, 32 (1966) 49-62, 32 (1966) 157-172.
10. HJW Мюллер, Дж. Рейн Ангью. Математика. 211 (1962) 33-47.
11. HJW Мюллер, Дж. Рейн Ангью. Математика. 212 (1963) 26-48.
12. HJW Мюллер-Кирстен (2012), Введение в квантовую механику: уравнение Шредингера и интеграл по траектории , 2-е изд., World Scientific , ISBN 978-9814397742 . Глава 18 об ангармонических потенциалах. 
13. «Введение в динамику коллоидов» , Дж. К. Дхонт, ссылка на книги Google.
14. Закконе, А.; Джентили, Д.; Ву, Х.; Морбиделли, М. (2009). «Теория активированных процессов при сдвиге с применением к сдвиговой агрегации коллоидов». Физический обзор E . 80 (5): 051404. arXiv : 0906.4879 . Бибкод : 2009PhRvE..80e1404Z. doi : 10.1103/PhysRevE.80.051404. hdl : 2434/653702 . PMID  20364982. S2CID  22763509.
15. Банетта, Л.; Закконе, А. (2019). «Радиальная функция распределения жидкостей Леннарда-Джонса в сдвиговых потоках из промежуточной асимптотики». Физический обзор E . 99 (5): 052606. arXiv : 1901.05175 . Бибкод : 2019PhRvE..99e2606B. doi : 10.1103/PhysRevE.99.052606. PMID  31212460. S2CID  119011235.
16. Банетта, Л.; Закконе, А. (2020). «Парная корреляционная функция коллоидных систем, стабилизированных зарядом, в условиях сдвига». Коллоидная и полимерная наука . 298 (7): 761–771. arXiv : 2006.00246 . дои : 10.1007/s00396-020-04609-4 .