Правила Вудворда-Хоффмана

Свод правил, касающихся перициклических реакций

Термолиз преобразует 1 в геометрический изомер 2 ( E , E ) , а 3 — в изомер 4 ( E , Z ) .

Правила Вудворда–Хоффмана (или правила перициклического отбора ) ^[1] представляют собой набор правил, разработанных Робертом Бернсом Вудвордом и Роальдом Хоффманом для рационализации или предсказания определенных аспектов стереохимии и энергии активации перициклических реакций , важного класса реакций в органической химии . Правила берут начало в определенных симметриях орбитальной структуры молекулы , которые сохраняет любой молекулярный гамильтониан . Следовательно, любая реакция, нарушающая симметрию, должна быть тесно связана с окружающей средой ; это накладывает энергетический барьер на ее возникновение, и такие реакции называются запрещенными по симметрии . Их противоположности — разрешенные по симметрии .

Хотя барьер, налагаемый симметрией, часто является огромным (до ок. 5 эВ или 480 кДж/моль в случае запрещенного [2+2] циклоприсоединения), запрет не является абсолютным, и запрещенные симметрией реакции все еще могут иметь место, если другие факторы (например, снятие напряжения) благоприятствуют реакции. Аналогично, разрешенная симметрией реакция может быть вытеснена непреодолимым энергетическим барьером, возникающим из-за факторов, не связанных с орбитальной симметрией. Все известные случаи только поверхностно нарушают правила; вместо этого различные части механизма становятся асинхронными , и каждый шаг соответствует правилам.

Предыстория и терминология

Перициклическая реакция — это органическая реакция, протекающая через единое согласованное и циклическое переходное состояние , геометрия которого допускает непрерывное перекрытие цикла (π и/или σ) -орбиталей .

Термины конротаторный и дисротаторный описывают относительное направление вращения связи, участвующее в электроциклических реакциях открытия и закрытия кольца. В дисротаторном процессе два конца разрываемой или образующейся связи вращаются в противоположных направлениях (один по часовой стрелке, один против часовой стрелки); в конротаторном процессе они вращаются в одном направлении (оба по часовой стрелке или оба против часовой стрелки), процесс является конротаторным .

В конце концов, было признано, что термически стимулируемые перициклические реакции в целом подчиняются единому набору обобщенных правил отбора, в зависимости от числа электронов и топологии орбитальных взаимодействий. Ключевое понятие орбитальной топологии или фациальности было введено для объединения нескольких классов перициклических реакций в рамках единой концептуальной структуры. Короче говоря, набор смежных атомов и связанных с ними орбиталей, которые реагируют как единое целое в перициклической реакции, известен как компонент , и каждый компонент называется антарафациальным или супрафациальным в зависимости от того, находятся ли орбитальные доли, которые взаимодействуют во время реакции, на противоположной или той же стороне узловой плоскости соответственно. (Старые термины конротаторный и дисротаторный, которые применимы только к открытию и закрытию электроциклического кольца, включены в термины антарафациальный и супрафациальный соответственно в рамках этой более общей системы классификации.)

История

Вудворд и Хоффманн разработали правила перициклического отбора после выполнения обширных расчетов перекрытия орбиталей. В то время Вудворд хотел узнать, могут ли определенные электроциклические реакции помочь синтезировать витамин B ₁₂ . Химики знали, что такие реакции демонстрируют поразительную стереоспецифичность , но не могли предсказать, какой стереоизомер может выбрать реакция. В 1965 году Вудворд-Хоффманн поняли, что простой набор правил объясняет наблюдаемую стереоспецифичность на концах сопряженных полиенов с открытой цепью при нагревании или облучении. В своей оригинальной публикации ^[2] они суммировали экспериментальные данные и молекулярный орбитальный анализ следующим образом:

• В системе с открытой цепью, содержащей 4 n π-электронов , орбитальная симметрия самой высокой занятой молекулярной орбитали такова, что связывающее взаимодействие между концами должно включать перекрытие между орбитальными оболочками на противоположных гранях системы, а это может быть достигнуто только в конротационном процессе.
• В открытых системах, содержащих (4 n + 2) π-электронов , терминальное связывающее взаимодействие внутри молекул в основном состоянии требует перекрытия орбитальных оболочек на одной и той же грани системы, что достигается только путем дисротационных смещений.
• В фотохимической реакции электрон в ВЗМО реагента переходит в возбужденное состояние, что приводит к изменению конечных соотношений симметрии и стереоспецифичности.

В 1969 году они использовали корреляционные диаграммы для формулировки обобщенного перициклического правила отбора, эквивалентного тому, которое теперь связано с их именем: перициклическая реакция допускается, если сумма числа супрафациальных 4 q + 2 компонентов и числа антарафациальных 4 r компонентов нечетна.

В течение следующих четырех лет Говард Циммерман ^{[3] [4]} и Майкл Дж. С. Дьюар ^{[5] [6]} предложили столь же общую концептуальную структуру: концепцию Мёбиуса-Хюккеля , или теорию ароматического переходного состояния . В подходе Дьюара-Циммермана топология перекрытия орбиталей (Хюккеля или Мёбиуса) и число электронов (4 n + 2 или 4 n ) приводит либо к ароматическому, либо к антиароматическому переходному состоянию.

Между тем, Кеничи Фукуи ^{[7] [8]} проанализировал граничные орбитали таких систем. Процесс, в котором взаимодействие HOMO-LUMO является конструктивным (приводит к чистому связывающему взаимодействию), является благоприятным и считается разрешенным симметрией, в то время как процесс, в котором взаимодействие HOMO-LUMO является неконструктивным (приводит к связывающим и антисвязывающим взаимодействиям, которые отменяют друг друга), является неблагоприятным и считается запрещенным симметрией.

Хотя концептуально они различны, теория переходного состояния ароматики (Циммерман и Дьюар), пограничная теория молекулярных орбиталей (Фукуи) и сохранение орбитальной симметрии (Вудворд и Хоффман) делают идентичные предсказания. Правила Вудворда-Хоффмана иллюстрируют силу теории молекулярных орбиталей ^[9] и действительно помогли продемонстрировать, что полезные химические результаты могут возникнуть из орбитального анализа . Это открытие принесло Хоффману и Фукуи Нобелевскую премию по химии 1981 года ^[10] К тому времени Вудворд умер и поэтому не имел права на премию.

Наглядные примеры

Показательно взаимопревращение модельных производных циклобутена и бутадиена в термических (нагревание) и фотохимических ( ультрафиолетовое облучение) условиях.

Правила Вудворда-Хоффмана применимы к любому направлению перициклического процесса. Из-за присущей производным циклобутенового цикла деформации равновесие между циклобутеном и 1,3-бутадиеном лежит далеко справа. Следовательно, в термических условиях раскрытие цикла циклобутена в 1,3-бутадиен сильно благоприятствует термодинамике. С другой стороны, при облучении ультрафиолетовым светом достигается фотостационарное состояние , состав которого зависит как от поглощения, так и от квантового выхода прямой и обратной реакций на определенной длине волны. Из-за различных степеней сопряжения 1,3-бутадиенов и циклобутенов только 1,3-бутадиен будет иметь значительное поглощение на более высоких длинах волн, предполагая отсутствие других хромофоров. Следовательно, облучение 1,3-бутадиена на такой длине волны может привести к высокой конверсии в циклобутен. Термолиз транс - 1,2,3,4-тетраметил-1-циклобутена ( 1 ) дал только один геометрический изомер, ( E , E )-3,4-диметил-2,4-гексадиен ( 2 ); геометрические изомеры ( Z , Z ) и ( E , Z ) не были обнаружены в смеси продуктов. Аналогично, термолиз цис -1,2,3,4-тетраметил-1-циклобутена ( 3 ) дал только ( E , Z ) изомер 4 . ^[11] В обеих реакциях раскрытия кольца углероды на концах разрывающейся σ-связи вращаются в одном и том же направлении. ^[12] С другой стороны, противоположный стереохимический ход наблюдался при фотохимической активации: когда родственное соединение ( E , E )-2,4-гексадиен ( 5 ) подвергалось воздействию света, цис -3,4-диметил-1-циклобутен ( 6 ) образовывался исключительно в результате электроциклического замыкания кольца. ^[13] Для этого требуется, чтобы концы π-системы вращались в противоположных направлениях для образования новой σ-связи. Термолиз 6 следует тому же стереохимическому ходу, что и 3 : электроциклическое раскрытие кольца приводит к образованию ( E , Z )-2,4-гексадиена ( 7 ), а не 5. [ ^14]

Некоторые термические и фотохимические взаимопревращения замещенных циклобутенов и бутадиенов, демонстрирующие конротаторное (синий) и дисротаторное (красный) поведение.

Правила Вудворда-Хоффмана объясняют эти результаты посредством перекрытия орбит:

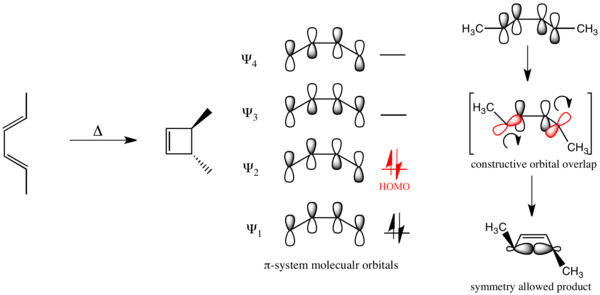
В случае фотохимически управляемого электроциклического замыкания кольца бута-1,3-диена электронное продвижение приводит к превращению в ВЗМО, и механизм реакции должен быть дисротационным. ${\displaystyle \Psi _{3}}$

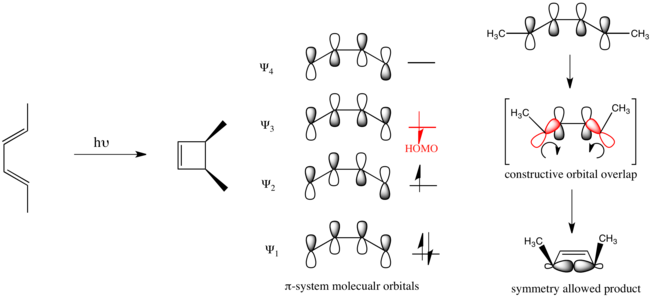
Напротив, при электроциклическом замыкании кольца замещенного гекса-1,3,5-триена, изображенного ниже, реакция протекает по дисротационному механизму.

Правило

Правила Вудворда-Хоффмана можно кратко сформулировать одним предложением: ^[15]

Обобщенное перициклическое правило отбора. Перициклический процесс в основном состоянии, включающий N электронных пар и A антарафациальных компонентов, является симметрийно разрешенным тогда и только тогда, когда N + A нечетно.

Перициклический процесс в основном состоянии вызывается добавлением тепловой энергии (т. е. нагреванием системы, что обозначается как Δ ). Напротив, перициклический процесс в возбужденном состоянии происходит, если реагент переводится в электронно-возбужденное состояние путем активации ультрафиолетовым светом (т. е. облучением системы, что обозначается как h ν ). Однако важно признать, что рабочий механизм формально перициклической реакции, происходящей при фотохимическом облучении, как правило, не так прост или ясен, как предполагает эта дихотомия. Обычно возможны несколько режимов электронного возбуждения, и электронно-возбужденные молекулы могут подвергаться межсистемному переходу , безызлучательному распаду или релаксировать до неблагоприятной равновесной геометрии до того, как может произойти перициклический процесс в возбужденном состоянии. Таким образом, многие кажущиеся перициклические реакции, происходящие при облучении, на самом деле считаются ступенчатыми процессами с участием бирадикальных промежуточных продуктов. Тем не менее, часто наблюдается, что правила перициклического отбора меняются на противоположные при переключении с термической на фотохимическую активацию. Это можно рационализировать, рассмотрев корреляцию первых электронных возбужденных состояний реагентов и продуктов. Хотя это скорее полезная эвристика, чем правило, можно сформулировать соответствующий обобщенный принцип отбора для фотохимических перициклических реакций:

Перициклический процесс с участием N электронных пар и A антарафациальных компонентов часто оказывается предпочтительным в фотохимических условиях, если N + A четное.

Известны также перициклические реакции с участием нечетного числа электронов. Что касается применения обобщенного перициклического правила отбора, то эти системы в целом можно рассматривать так, как если бы в них участвовало на один электрон больше. ^[16]

На языке теории ароматических переходных состояний правила Вудворда–Хоффмана можно переформулировать следующим образом: перициклическое переходное состояние, включающее (4 n + 2) электронов с топологией Хюккеля или 4 n электронов с топологией Мёбиуса, является ароматическим и разрешенным, тогда как перициклическое переходное состояние, включающее 4 n -электронов с топологией Хюккеля или (4 n + 2) -электронов с топологией Мёбиуса, является антиароматическим и запрещенным.

Диаграммы корреляции

Лонге-Хиггинс и Э. У. Абрахамсон показали, что правила Вудворда–Хоффмана лучше всего вывести, изучив диаграмму корреляции данной реакции. ^{[17] [16] [18] [19]} Элемент симметрии — это точка отсчета (обычно плоскость или линия), относительно которой объект симметричен относительно операции симметрии. Если элемент симметрии присутствует на протяжении всего механизма реакции (реагент, переходное состояние и продукт), он называется сохраняющимся элементом симметрии. Тогда на протяжении всей реакции симметрия молекулярных орбиталей относительно этого элемента должна сохраняться. То есть молекулярные орбитали, симметричные относительно элемента симметрии в исходном материале, должны быть соотнесены (преобразованы) в орбитали, симметричные относительно этого элемента в продукте. И наоборот, то же самое утверждение справедливо для антисимметрии относительно сохраняющегося элемента симметрии. Диаграмма корреляции молекулярных орбиталей соотносит молекулярные орбитали исходных материалов и продукта на основе сохранения симметрии. Из диаграммы корреляции молекулярных орбиталей можно построить диаграмму корреляции электронных состояний , которая коррелирует электронные состояния (т.е. основное состояние и возбужденные состояния) реагентов с электронными состояниями продуктов. Диаграммы корреляции затем можно использовать для прогнозирования высоты барьеров переходного состояния. ^[20]

Хотя орбитальная «симметрия» используется в качестве инструмента для построения диаграмм орбитальной и корреляционной схем состояний, абсолютное наличие или отсутствие элемента симметрии не имеет решающего значения для определения того, разрешена или запрещена реакция. То есть введение простого заместителя, который формально нарушает плоскость или ось симметрии (например, метильной группы), обычно не влияет на оценку того, разрешена или запрещена реакция. Вместо этого симметрия, присутствующая в незамещенном аналоге, используется для упрощения построения диаграмм орбитальной корреляции и избегания необходимости выполнять вычисления. ^[21] Только фазовые соотношения между орбиталями важны при оценке того, разрешена или запрещена реакция по «симметрии». Более того, орбитальные корреляции все еще могут быть сделаны, даже если нет сохраняющихся элементов симметрии (например, 1,5-сигматропных сдвигов и еновых реакций). По этой причине анализы Вудворда–Хоффмана, Фукуи и Дьюара–Циммермана одинаково широко применимы, хотя определенный подход может быть проще или интуитивно понятнее в применении, чем другой, в зависимости от реакции, которую требуется проанализировать.

Электроциклические реакции

Переходное состояние конротаторного замыкания имеет симметрию C2 _, тогда как переходное состояние дисротаторного открытия имеет зеркальную симметрию.

МО бутадиена показаны с элементом, с которым они симметричны. Они антисимметричны по отношению к другому.

Принимая во внимание электроциклическое замыкание кольца замещенного 1,3-бутадиена, реакция может протекать либо по конротаторному , либо по дисротаторному механизму реакции. Как показано слева, в конротаторном переходном состоянии имеется ось симметрии C 2 , а в дисротаторном переходном состоянии имеется зеркальная плоскость симметрии σ . Чтобы соотнести орбитали исходного материала и продукта, необходимо определить, являются ли молекулярные орбитали симметричными или антисимметричными относительно этих элементов симметрии. Молекулярные орбитали π-системы бутадиена показаны справа вместе с элементом симметрии, с которым они симметричны. Они антисимметричны относительно друг друга. Например, Ψ ₂ 1,3-бутадиена симметрична относительно вращения на 180 ^o вокруг оси C ₂ и антисимметрична относительно отражения в зеркальной плоскости.

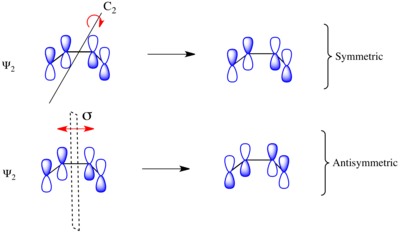
Ψ ₁ и Ψ ₃ симметричны относительно зеркальной плоскости, поскольку знак p-орбитальных лепестков сохраняется при преобразовании симметрии. Аналогично, Ψ ₁ и Ψ ₃ антисимметричны относительно оси C ₂ , поскольку вращение равномерно инвертирует знак p-орбитальных лепестков. Наоборот, Ψ ₂ и Ψ ₄ симметричны относительно оси C ₂ и антисимметричны относительно зеркальной плоскости σ.

Тот же анализ можно провести для молекулярных орбиталей циклобутена. Результат обеих операций симметрии на каждой из МО показан слева. Поскольку орбитали σ и σ ^* полностью лежат в плоскости, содержащей C _{2 ,} перпендикулярной σ, они равномерно симметричны и антисимметричны (соответственно) обоим элементам симметрии. С другой стороны, π симметричен относительно отражения и антисимметричен относительно вращения, в то время как π ^* антисимметричен относительно отражения и симметричен относительно вращения.

Корреляционные линии проводятся для соединения молекулярных орбиталей в исходном материале и продукте, которые имеют одинаковую симметрию относительно сохраняющегося элемента симметрии. В случае конротаторного 4-электронного электроциклического замыкания кольца 1,3-бутадиена самая низкая молекулярная орбиталь Ψ ₁ асимметрична (A) относительно оси C ₂ . Таким образом, эта молекулярная орбиталь коррелирует с π-орбиталью циклобутена, самой низкой энергетической орбиталью, которая также является (A) относительно оси C ₂ . Аналогично, Ψ ₂ , которая симметрична (S) относительно оси C ₂ , коррелирует с σ циклобутена. Последние две корреляции существуют между антисимметричными (A) молекулярными орбиталями Ψ ₃ и σ ^* , и симметричными (S) молекулярными орбиталями Ψ ₄ и π ^* . ^[16]

Корреляционная диаграмма реакции электроциклизации 4 электронов с конротационным механизмом.

Аналогично существует корреляционная диаграмма для дисротационного механизма. В этом механизме элементом симметрии, который сохраняется на протяжении всего механизма, является σ-зеркальная плоскость отражения. Здесь МО с самой низкой энергией Ψ ₁ 1,3-бутадиена симметрична относительно плоскости отражения и, как таковая, коррелирует с симметричной σ МО циклобутена. Аналогично коррелируют более высокоэнергетические пары симметричных молекулярных орбиталей Ψ ₃ и π. Что касается асимметричных молекулярных орбиталей, то более низкоэнергетическая пара Ψ ₂ и π ^* образует корреляционную пару, как и Ψ ₄ и σ ^* . ^[16]

Корреляционная диаграмма реакции электроциклизации 4 электронов с дисротационным механизмом.

Оценивая два механизма, предсказывается, что конротаторный механизм будет иметь более низкий барьер , поскольку он преобразует электроны из орбиталей основного состояния реагентов (Ψ ₁ и Ψ ₂ ) в орбитали основного состояния продукта (σ и π). Наоборот, дисротаторный механизм заставляет преобразовывать орбиталь Ψ ₁ в орбиталь σ, а орбиталь Ψ ₂ в орбиталь π ^* . Таким образом, два электрона в орбитали основного состояния Ψ ₂ переносятся на возбужденную антисвязывающую орбиталь, создавая дважды возбужденное электронное состояние циклобутена. Это приведет к значительно более высокому барьеру переходного состояния для реакции. ^[16]

Первое возбужденное состояние (ES-1) бутадиена.

Однако, поскольку реакции происходят не между разобщенными молекулярными орбиталями, а между электронными состояниями, окончательный анализ включает диаграммы корреляции состояний. Диаграмма корреляции состояний коррелирует общую симметрию электронных состояний в исходном материале и продукте. Основное состояние 1,3-бутадиена, как показано выше, имеет 2 электрона в Ψ ₁ и 2 электрона в Ψ ₂ , поэтому оно представлено как Ψ ₁ ² Ψ ₂ ² . Общая симметрия состояния является произведением симметрий каждой заполненной орбитали с множественностью для дважды заполненных орбиталей. Таким образом, поскольку Ψ ₁ асимметрична относительно оси C ₂ , а Ψ ₂ симметрична, общее состояние представлено как A ² S ² . Чтобы понять, почему этот конкретный продукт математически является общим S, можно представить S как (+1), а A как (−1). Это вытекает из того факта, что знаки долей p-орбиталей умножаются на (+1), если они симметричны относительно преобразования симметрии (т. е. не изменяются), и умножаются на (−1), если они антисимметричны относительно преобразования симметрии (т. е. инвертируются). Таким образом, A ² S ² =(−1) ² (+1) ² =+1=S. Первое возбужденное состояние (ES-1) образуется при продвижении электрона из HOMO в LUMO и, таким образом, представляется как Ψ ₁ ² Ψ ₂ Ψ ₃ . Поскольку Ψ ₁ — это A, Ψ ₂ — это S, а Ψ ₃ — это A, симметрия этого состояния задается как A ² SA=A. Теперь, рассматривая электронные состояния продукта, циклобутена, основное состояние задается как σ ² π ² , которое имеет симметрию S ² A ² =S. Первое возбужденное состояние (ES-1') снова образуется в результате перехода электрона из HOMO в LUMO , поэтому в этом случае оно представлено как σ ² ππ ^* . Симметрия этого состояния S ² AS=A.

Основное состояние Ψ ₁ ² Ψ ₂ ² 1,3-бутадиена коррелирует с основным состоянием σ ² π ² циклобутена, как показано на диаграмме корреляции МО выше. Ψ ₁ коррелирует с π, а Ψ ₂ коррелирует с σ. Таким образом, орбитали, составляющие Ψ ₁ ² Ψ ₂ ^2, должны трансформироваться в орбитали, составляющие σ ² π ^2, по конротаторному механизму. Однако состояние ES-1 не коррелирует с состоянием ES-1', поскольку молекулярные орбитали не трансформируются друг в друга в соответствии с требованием симметрии, видимым на диаграмме корреляции молекулярных орбиталей. Вместо этого, поскольку Ψ ₁ коррелирует с π, Ψ ₂ коррелирует с σ, а Ψ ₃ коррелирует с σ ^* , состояние Ψ ₁ ² Ψ ₂ Ψ ₃ пытается трансформироваться в π ² σσ ^* , которое является другим возбужденным состоянием. Таким образом, ES-1 пытается коррелировать с ES-2'=σπ ² σ ^* , которое имеет более высокую энергию, чем Es-1'. Аналогично ES-1'=σ ² ππ ^* пытается коррелировать с ES-2=Ψ ₁ Ψ ₂ ² Ψ ₄ . Эти корреляции на самом деле не могут иметь место из-за квантово-механического правила, известного как правило избегаемого пересечения . Оно гласит, что энергетические конфигурации одной и той же симметрии не могут пересекаться на диаграмме корреляции энергетических уровней. Короче говоря, это вызвано смешиванием состояний одной и той же симметрии, когда они достаточно близки по энергии. Поэтому вместо этого формируется высокий энергетический барьер между вынужденным преобразованием ES-1 в ES-1'. На диаграмме ниже предпочтительные по симметрии корреляции показаны пунктирными линиями, а жирные кривые линии указывают на фактическую корреляцию с высоким энергетическим барьером. ^{[16] [20]}

Диаграмма корреляции состояний электроциклизации 4 электронов с конротационным механизмом.

Тот же анализ можно применить к дисротационному механизму для создания следующей диаграммы корреляции состояний. ^{[16] [20]}

Диаграмма корреляции состояний электроциклизации 4 электронов при дисротационном механизме.

Таким образом, если молекула находится в основном состоянии, она будет проходить через конротаторный механизм (т. е. под термическим контролем), чтобы избежать электронного барьера. Однако, если молекула находится в первом возбужденном состоянии (т. е. под фотохимическим контролем), электронный барьер присутствует в конротаторном механизме, и реакция будет проходить через дисротаторный механизм. Они не полностью различимы, поскольку и конротаторный, и дисротаторный механизмы лежат на одной и той же потенциальной поверхности. Таким образом, более правильным утверждением является то, что когда молекула в основном состоянии исследует поверхность потенциальной энергии, она с большей вероятностью достигнет активационного барьера, чтобы пройти через конротаторный механизм. ^[20]

Реакции циклоприсоединения

Правила Вудворда–Хоффмана также могут объяснить бимолекулярные реакции циклоприсоединения с помощью корреляционных диаграмм. ^[22] Циклоприсоединение [ _π p + _π q ] объединяет два компонента, один с p π-электронами, а другой с q π-электронами. Реакции циклоприсоединения далее характеризуются как супрафациальные (s) или антарафациальные (a) по отношению к каждому из π-компонентов. ( См. ниже «Общая формулировка» для подробного описания обобщения обозначения WH для всех перициклических процессов .)

[2+2] Циклоприсоединения

Для обычных алкенов [2+2] циклоприсоединения наблюдаются только при фотохимической активации.

Обоснование ненаблюдения термических [2+2] циклоприсоединений начинается с анализа четырех возможных стереохимических последствий для [2+2] циклоприсоединения: [ _π 2 _s + _π 2 _s ], [ _π 2 _a + _π 2 _s ], [ _π 2 _s + _π 2 _a ], [ _π 2 _a + _π 2 _a ]. Геометрически наиболее правдоподобный режим [ _π 2 _s + _π 2 _s ] запрещен в термических условиях, в то время как подходы [ _π 2 _a + _π 2 _s ], [ _π 2 _s + _π 2 _a ] разрешены с точки зрения симметрии, но редки из-за неблагоприятного напряжения и стерического профиля. ^[16]

Циклоприсоединение [2s ₊ 2s _] сохраняет стереохимию.

Элементы симметрии циклоприсоединения [2+2].

Рассмотрим циклоприсоединение [ _π 2 _s + _π 2 _s ]. Этот механизм приводит к сохранению стереохимии в продукте, как показано справа. В исходных материалах, переходном состоянии и продукте присутствуют два элемента симметрии: σ ₁ и σ ₂ . σ ₁ — это зеркальная плоскость между компонентами, перпендикулярная p-орбиталям ; σ ₂ разделяет молекулы пополам перпендикулярно σ-связям . ^[22] Оба они являются элементами локальной симметрии в случае, если компоненты не идентичны.

Чтобы определить симметрию и асимметрию относительно σ ₁ и σ ₂ , исходные молекулярные орбитали материала должны рассматриваться в тандеме. На рисунке справа показана диаграмма корреляции молекулярных орбиталей для циклоприсоединения [ _π 2 _s + _π 2 _s ]. Две π и π ^* молекулярные орбитали исходных материалов характеризуются своей симметрией относительно сначала σ ₁ , а затем σ ₂ . Аналогично, σ и σ ^* молекулярные орбитали продукта характеризуются своей симметрией. На диаграмме корреляции молекулярные орбитали, преобразующиеся в ходе реакции, должны сохранять симметрию молекулярных орбиталей. Таким образом, π _SS коррелирует с σ _SS , π _AS коррелирует с σ ^* _AS , π ^* _SA коррелирует с σ _SA , и, наконец, π ^* _AA коррелирует с σ ^* _AA . Из-за сохранения орбитальной симметрии связывающая орбиталь π _AS вынуждена коррелировать с антисвязывающей орбиталью σ ^* _AS . Таким образом, предсказывается высокий барьер. ^{[16] [20] [22]}

Это точно показано на диаграмме корреляции состояний ниже. ^{[16] [20]} Основное состояние в исходных материалах — это электронное состояние, в котором π _SS и π _AS оба заселены дважды, т. е. состояние (SS) ² (AS) ² . Таким образом, это состояние пытается коррелировать с электронным состоянием в продукте, в котором и σ _SS , и σ ^* _AS оба заселены дважды, т. е. состояние (SS) ² (AS) ² . Однако это состояние не является ни основным состоянием (SS) ² (SA) ² циклобутана, ни первым возбужденным состоянием ES-1'=(SS) ² (SA)(AS), в котором электрон продвигается из HOMO в LUMO.

[4+2] циклоприсоединения

Зеркальная плоскость является единственным сохраняющимся элементом симметрии [4+2]-циклоприсоединения Дильса-Альдера.

Примером [4+2] циклоприсоединения является реакция Дильса-Альдера . Простейшим случаем является реакция 1,3-бутадиена с этиленом с образованием циклогексена .

В этом преобразовании сохраняется один элемент симметрии – зеркальная плоскость, проходящая через центр реагентов, как показано слева. Молекулярные орбитали реагентов представляют собой набор {Ψ ₁ , Ψ ₂ , Ψ ₃ , Ψ ₄ } молекулярных орбиталей 1,3-бутадиена, показанных выше, вместе с π и π ^* этилена. Ψ ₁ симметрична, Ψ ₂ антисимметрична, Ψ ₃ симметрична, а Ψ ₄ антисимметрична относительно зеркальной плоскости. Аналогично π симметрична, а π ^* антисимметрична относительно зеркальной плоскости.

Молекулярные орбитали продукта представляют собой симметричные и антисимметричные комбинации двух вновь образованных связей σ и σ ^* и связей π и π ^* , как показано ниже.

Корреляция пар орбиталей в исходных материалах и продукте с одинаковой симметрией и повышение энергии дает диаграмму корреляции справа. Поскольку это преобразует связывающие молекулярные орбитали основного состояния исходных материалов в связывающие молекулярные орбитали основного состояния продукта консервативным симметрийным образом, это, как предсказывается, не будет иметь большого энергетического барьера, присутствующего в реакции основного состояния [2+2] выше.

Чтобы сделать анализ точным, можно построить диаграмму корреляции состояний для общего [4+2]-циклоприсоединения. ^[20] Как и прежде, основное состояние - это электронное состояние, изображенное на диаграмме корреляции молекулярных орбиталей справа. Его можно описать как Ψ ₁ ² π ² Ψ ₂ ² , полной симметрии S ² S ² A ² =S. Это коррелирует с основным состоянием циклогексена σ S _σ A _π 2 ^, которое также является S ² S ² A ² =S. Таким образом, эта реакция основного состояния не имеет высокого барьера, налагаемого симметрией.

Можно также построить корреляции возбужденного состояния, как это сделано выше. Здесь существует высокий энергетический барьер для фотоиндуцированной реакции Дильса-Альдера в топологии супрафациально-супрафациальной связи из-за избегаемого пересечения, показанного ниже.

Реакции группового переноса

Перенос пары атомов водорода от этана к пердейтероэтилену.

Симметрично наложенные высоты барьеров реакций переноса групп также можно проанализировать с помощью корреляционных диаграмм. Модельной реакцией является перенос пары атомов водорода от этана к пердейтероэтилену, показанный справа.

Единственным сохраняющимся элементом симметрии в этой реакции является зеркальная плоскость, проходящая через центр молекул, как показано слева.

Сохраняющаяся зеркальная плоскость в реакции переноса.

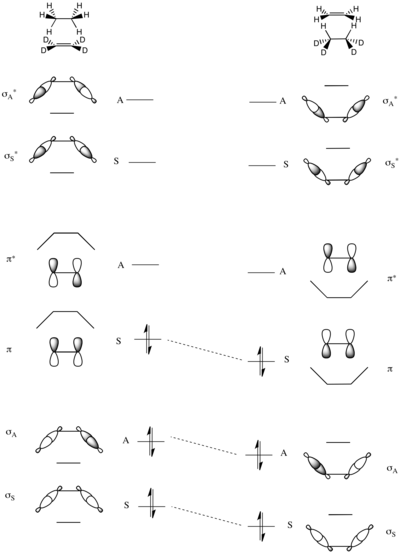
Молекулярные орбитали системы построены как симметричные и антисимметричные комбинации связей σ и σ ^* C–H в этане и связей π и π ^* в дейтерозамещенном этене. Таким образом, МО с самой низкой энергией представляет собой симметричную сумму двух σ-связей C–H (σ _S ), за которой следует антисимметричная сумма (σ _A ). Две МО с самой высокой энергией образованы из линейных комбинаций антисвязей σ _CH – самой высокой является антисимметричная σ ^* _A , которой предшествует симметричная σ ^* _A с немного более низкой энергией. В середине энергетической шкалы находятся две оставшиеся МО, которые являются π _CC и π ^* _CC этена.

Полная диаграмма корреляции молекулярных орбиталей строится путем сопоставления пар симметричных и асимметричных МО с возрастающей полной энергией, как объяснено выше. Как можно видеть на соседней диаграмме, поскольку связывающие орбитали реагентов точно коррелируют со связывающими орбиталями продуктов, эта реакция не должна иметь высокий барьер, налагаемый электронной симметрией. ^{[16] [20]}

Правила отбора

Используя диаграммы корреляции, можно вывести правила отбора для следующих обобщенных классов перициклических реакций. Каждый из этих конкретных классов далее обобщается в обобщенных правилах Вудворда–Хоффмана. Более инклюзивные дескрипторы топологии связи антарафациальный и супрафациальный включают термины конротаторный и дисротаторный соответственно. Антарафациальный относится к созданию или разрыву связи через противоположную грань π-системы, p-орбитали или σ-связи, тогда как супрафациальный относится к процессу, происходящему через ту же грань. Супрафациальное преобразование в хиральном центре сохраняет стереохимию, тогда как антарафациальное преобразование меняет стереохимию.

Электроциклические реакции

Правило отбора реакций электроциклизации приведено в исходной формулировке правил Вудворда–Хоффмана. Если обобщенное электроциклическое замыкание кольца происходит в полиене с 4 n π-электронами, то оно является конротаторным в термических условиях и дисротаторным в фотохимических условиях. Наоборот, в полиене с 4 n + 2 π-электронами электроциклическое замыкание кольца является дисротаторным в термических условиях и конротаторным в фотохимических условиях.

Этот результат может быть получен либо с помощью анализа FMO, основанного на знаке p-орбитальных долей HOMO полиена, либо с помощью корреляционных диаграмм. Если сначала взять первую возможность, в основном состоянии, если полиен имеет 4 n электронов, внешние p-орбитали HOMO, которые образуют σ-связь в электроциклизованном продукте, имеют противоположные знаки. Таким образом, конструктивное перекрытие производится только при конротаторном или антарафациальном процессе. Наоборот, для полиена с 4 n + 2 электронами внешние p-орбитали основного состояния HOMO имеют тот же знак. Таким образом, конструктивное перекрытие орбиталей происходит при дисротаторном или супрафациальном процессе. ^[2]

Электроциклическая реакция с 4n-электронами приводит к конструктивному перекрытию орбиталей HOMO, если она является конротаторной, тогда как электроциклическая реакция с 4n+2 приводит к конструктивному перекрытию, если она является дисротаторной.

Кроме того, корреляционная диаграмма для любой электроциклической реакции 4 n будет напоминать диаграмму для 4-электронной циклизации 1,3-бутадиена, в то время как корреляционная диаграмма любой электроциклической реакции 4 n + 2 электрона будет напоминать корреляционную диаграмму для 6-электронной циклизации 1,3,5-гексатриена. ^[16]

Это обобщено в следующей таблице:

Реакции сигматропной перегруппировки

Общую сигматропную перегруппировку можно классифицировать как порядок [ i , j ], что означает, что σ-связь, изначально между атомами, обозначенными 1 и 1', соседствующими с одной или несколькими π-системами, смещается на связь между атомами i и j . Таким образом, она перемещает ( i − 1), ( j − 1) атомов от своего исходного положения.

Формальный анализ симметрии с помощью корреляционных диаграмм бесполезен при изучении сигматропных перестроек, поскольку в переходном состоянии, как правило, присутствуют только элементы симметрии. За исключением особых случаев (например, [3,3]-перестроек), нет элементов симметрии, которые сохраняются при прохождении координаты реакции. ^{[16] [20]} Тем не менее, орбитальные корреляции между исходными материалами и продуктами все еще могут быть проанализированы, и корреляции орбиталей исходных материалов с орбиталями продуктов высокой энергии, как обычно, приведут к процессам, «запрещенным симметрией». Однако подход, основанный на FMO (или анализ Дьюара-Циммермана), более прост в применении.

В [1,j]-сигматропных перегруппировках, если 1+j = 4n, то супра/антара термически разрешена, а если 1+j = 4n+2, то супра/супра или антара/антара термически разрешена.

Один из наиболее распространенных классов сигматропных сдвигов классифицируется как [1, j ], где j нечетно. Это означает, что один конец σ-связи мигрирует ( j − 1) связей через π-систему, в то время как другой конец не мигрирует. Это реакция с участием j + 1 электронов: j − 1 из π-системы и 2 из σ-связи. Используя анализ FMO, [1, j ]-сигматропные перестройки разрешены, если переходное состояние имеет конструктивное перекрытие между мигрирующей группой и принимающей p-орбиталью HOMO. В [1, j ]-сигматропных перестройках, если j + 1 = 4 n , то супра/антара термически разрешены, а если j + 1 = 4 n + 2, то супра/супра или антара/антара термически разрешены. ^[20]

Другим распространенным классом сигматропных перегруппировок являются [3,3], в частности перегруппировки Коупа и Кляйзена . Здесь конструктивные взаимодействия должны быть между HOMO двух фрагментов аллильного радикала в переходном состоянии. Основное состояние HOMO Ψ ₂ фрагмента аллила показано ниже. Поскольку конечные p-орбитали имеют противоположный знак, эта реакция может происходить либо в топологии супра/супра, либо в топологии антара/антара. ^[20]

[3,3]-сигматропная реакция в основном состоянии допускается посредством топологии супра/супра или антара/антара.

Правила отбора для [ i , j ]-сигматропной перегруппировки следующие:

• Для супра/супра или антара/антара [ i , j ]-сигматропных сдвигов, если i + j = 4 n + 2, они термически разрешены, а если i + j = 4 n, они фотохимически разрешены.
• Для супра/антара [ i , j ]-сигматропных сдвигов, если i + j = 4 n , они термически разрешены, а если i + j = 4 n + 2 , они фотохимически разрешены.

Это обобщено в следующей таблице:

Реакции циклоприсоединения

Общее [ p + q ]-циклоприсоединение — это согласованная реакция присоединения между двумя компонентами, один с p π-электронами, а другой с q π-электронами. Эта реакция симметрия разрешена при следующих условиях: ^[16]

• Для супра/супра или антара/антара циклоприсоединения термически разрешено, если p + q = 4 n + 2, и фотохимически разрешено, если p + q = 4 n.
• Для супра/антара циклоприсоединения термически разрешено, если p + q = 4 n и фотохимически разрешено, если p + q = 4 n + 2

Это обобщено в следующей таблице:

Реакции группового переноса

Общую реакцию переноса двойной группы, которая является синхронной, можно представить как взаимодействие между компонентом с p π электронами и компонентом с q π электронами, как показано на рисунке.

Обобщенная синхронная реакция двойной групповой передачи между компонентом с p π электронами и компонентом с q π электронами.

Тогда правила отбора такие же, как и для обобщенных реакций циклоприсоединения. ^[16] То есть

• Для двойных групповых переносов supra/supra или antara/antara, если p + q = 4 n + 2, это термически разрешено, а если p + q = 4 n, то это фотохимически разрешено.
• Для супра/антара двойных групповых переносов, если p + q = 4 n, это термически разрешено, а если p + q = 4 n + 2, то это фотохимически разрешено.

Это обобщено в следующей таблице:

Случай q = 0 соответствует термическому отщеплению «перенесенных» групп R. Имеются данные, что пиролитическое отщепление диводорода и этана из 1,4-циклогексадиена и 3,3,6,6-тетраметил-1,4-циклогексадиена, соответственно, представляет собой примеры этого типа перициклического процесса.

Реакцию ена часто классифицируют как тип процесса переноса группы, хотя она не включает перенос двух σ-связанных групп. Вместо этого переносится только одна σ-связь, в то время как вторая σ-связь образуется из разорванной π-связи. Как полностью супрафациальный процесс, включающий 6 электронов, он разрешен симметрией в термических условиях. Символ Вудворда-Хоффмана для реакции ена — [ _π 2 _s + _π 2 _s + _σ 2 _s ] ( см. ниже ).

Общая формулировка

Хотя правила Вудворда–Хоффмана были впервые сформулированы в терминах электроциклических процессов, в конечном итоге они были обобщены на все перициклические реакции, на что указывают сходство и закономерности в приведенных выше правилах отбора.

Конротационное движение является антарафациальным, а дисротационное — супрафациальным.

В обобщенных правилах Вудворда–Хоффмана все характеризуется в терминах антарафациальной и супрафациальной топологии связей. Термины конротаторный и дисротаторный достаточны для описания относительного направления вращения связей в электроциклических реакциях замыкания или размыкания кольца, как показано справа. Однако они не подходят для описания топологии образования и разрыва связей, происходящих в общей перициклической реакции. Как подробно описано ниже, в общей формулировке правил Вудворда–Хоффмана термины вращения связей конротаторный и дисротаторный включены в термины топологии связи (или фациальности) антарафациальный и супрафациальный соответственно. Эти дескрипторы можно использовать для характеристики топологии образования и разрыва связей, происходящих в любом перициклическом процессе.

Обозначение Вудворда-Хоффмана

Компонент — это любая часть молекулы или молекул, которые функционируют как единое целое в перициклической реакции. Компонент состоит из одного или нескольких атомов и любого из следующих типов связанных орбиталей:

• Изолированная p- или sp ^x - орбиталь (незаполненная или заполненная, символ ω)
• Сопряженная π-система (символ π)
• σ -связь (символ σ)

Электронное число компонента — это число электронов на орбитали(ях) компонента:

• Число электронов на незаполненной ω-орбитали (т. е. пустой p-орбитали) равно 0, тогда как число электронов на заполненной ω-орбитали (т. е. неподеленной паре) равно 2.
• Число электронов сопряженной π-системы с n двойными связями равно 2n ( или 2n + 2, если к ней присоединена (формальная) неподеленная пара из гетероатома или карбаниона).
• Число электронов в σ-связи равно 2.

Топология связи компонента может быть супрафациальной и антарафациальной:

• Связь является супрафациальной (символ: s), когда взаимодействия с π-системой или p-орбиталью происходят по одну и ту же сторону узловой плоскости (думайте о syn ). Для σ-связи это соответствует взаимодействиям, происходящим на двух «внутренних» лепестках или двух «внешних» лепестках связи.
• Связь является антарафациальной (символ: a), когда взаимодействия с π-системой или p-орбиталью происходят на противоположных сторонах узловой плоскости (представьте себе анти ). Для σ-связи это соответствует взаимодействиям, происходящим на одной «внутренней» и одной «внешней» долях связи.

Иллюстрация назначения орбитального перекрытия как супрафациального или антарафациального для общих перициклических компонентов.

Используя эту нотацию, всем перициклическим реакциям можно присвоить дескриптор, состоящий из ряда символов _σ/π/ω N _s/a , соединенных знаками + и заключенных в скобки, описывающих, по порядку, тип орбитали(ей), число электронов и топологию связи, задействованную для каждого компонента. Ниже приведены некоторые иллюстративные примеры:

• Реакция Дильса-Альдера ((4+2)-циклоприсоединение) имеет вид [ _π 4 _s + _π 2 _s ].
• 1,3-Диполярное циклоприсоединение озона и олефина на первой стадии _{озонолиза} ( (3+2)-циклоприсоединение) представляет собой [ _π 4 s + _π 2 _s ].
• Хелетропное присоединение диоксида серы к 1,3-бутадиену ((4+1)-хелетропное присоединение) равно [ _ω 0 _a + _π 4 _s ] + [ _ω 2 _s + _π 4 _s ]. ^[23]
• Перегруппировка Коупа ([3,3]-сигматропный сдвиг) равна [ _π 2 _s + _σ 2 _s + _π 2 _s ] или [ _π 2 _a + _σ 2 _s + _π 2 _a ].
• Миграция [1,3]-алкила с инверсией у углерода, открытая Берсоном ([1,3]-сигматропный сдвиг), равна [ _σ 2 _a + _π 2 _s ].
• Конротаторное электроциклическое замыкание кольца 1,3-бутадиена (4π-электроциклизация) представляет собой [ _π 4 _a ].
• Конротаторное электроциклическое раскрытие кольца циклобутена (обратная 4π-электроциклизация) представляет собой [ _σ 2 _a + _π 2 _s ] или [ _σ 2 _s + _π 2 _a ].
• Дисротационное электроциклическое замыкание кольца аниона 1,3-циклооктадиен-5-ида (6π-электроциклизация) представляет собой [ _π 6 _s ].
• Сдвиг Вагнера-Меервейна карбокатиона ( [1,2]-сигматропный сдвиг) равен [ _ω 0 _s + _σ 2 _s ].

Антарафациальный и супрафациальный связаны с (конротацией или инверсией) и (дисротацией или удержанием) соответственно. Один дескриптор может соответствовать двум перициклическим процессам, которые химически различны, что реакция и ее микроскопическая обратимость часто описываются двумя разными дескрипторами, и что один процесс может иметь более одного правильного дескриптора. Можно проверить, используя правило перициклического отбора, приведенное ниже, что все эти реакции являются разрешенными процессами.

Оригинальное заявление

Используя эту нотацию, Вудворд и Хоффман в своем обзоре 1969 года сформулировали общую формулировку для всех перициклических реакций следующим образом:

Перициклическое изменение основного состояния является симметрией разрешенным, когда общее число компонентов (4q+2) _s и (4r) _a нечетно. ^[16]

Здесь (4 q + 2) _s и (4 r ) _a относятся к супрафациальному (4 q + 2)-электронному и антарафациальному (4 r )-электронному компонентам соответственно. Более того, этот критерий следует интерпретировать как достаточный (указанный выше), а также необходимый (не указанный явно выше, см.: если и только если )

Вывод альтернативного утверждения

В качестве альтернативы общее утверждение можно сформулировать в терминах общего числа электронов, используя простые правила делимости путем прямого анализа двух случаев.

Сначала рассмотрим случай, когда общее число электронов равно 4n + 2:

4 n + 2 = a (4 q + 2) _s + b (4 p + 2) _a + c (4 t ) _s + d (4 r ) _a ,

где a , b , c , и d являются коэффициентами, указывающими количество каждого типа компонента. Это уравнение подразумевает, что один из, но не оба, a или b является нечетным, поскольку если a и b оба четные или оба нечетные, то сумма четырех членов равна 0 (mod 4).

Обобщенное утверждение правил Вудворда-Хоффмана гласит, что a + d нечетно, если реакция разрешена. Теперь, если a четно, то это означает, что d нечетно. Поскольку b в этом случае нечетно, число антарафациальных компонентов, b + d , четно. Аналогично, если a нечетно, то d четно. Поскольку b в этом случае четно, число антарафациальных компонентов, b + d , снова четно. Таким образом, независимо от первоначального предположения о четности для a и b , число антарафациальных компонентов четно, когда число электронов равно 4 n + 2. Наоборот, b + d нечетно.

В случае, когда общее число электронов равно 4n , аналогичные рассуждения (здесь опущены) приводят к выводу, что число антарафациальных компонентов b + d должно быть нечетным в разрешенном случае и четным в запрещенном случае.

Наконец, чтобы завершить аргументацию и показать, что этот новый критерий действительно эквивалентен исходному критерию, нужно также доказать обратные утверждения, а именно, что число антарафациальных компонентов b + d и число электронов (4 n + 2 или 4 n ) подразумевает четность a + d , которая задается правилами Вудворда-Хоффмана (нечетный для разрешенного, четный для запрещенного). Еще один раунд (несколько утомительного) анализа случаев легко покажет, что это так. Перициклическое правило отбора гласит:

Перициклический процесс с участием 4n+2 или 4n электронов термически разрешен тогда и только тогда, когда число участвующих антарафациальных компонентов четное или нечетное соответственно.

В этой формулировке число электронов относится ко всей реагирующей системе, а не к отдельным компонентам, как перечислено в исходном утверждении Вудворда и Хоффмана. На практике четное или нечетное число антарафациальных компонентов обычно означает ноль или один антарафациальный компонент соответственно, поскольку переходные состояния, включающие два или более антарафациальных компонентов, как правило, неблагоприятны из-за деформации. В качестве исключений некоторые внутримолекулярные реакции могут быть геометрически ограничены таким образом, что обеспечивает антарафациальную траекторию для нескольких компонентов. Кроме того, в некоторых случаях, например, перегруппировка Коупа, можно считать, что одна и та же (не обязательно напряженная) геометрия переходного состояния содержит два супра или два антарафациальных π компонента, в зависимости от того, как провести связи между орбитальными долями. (Эта неоднозначность является следствием соглашения, что перекрытие либо обеих внутренних, либо обеих внешних долей σ компонента можно считать супрафациальным.)

Эта альтернативная формулировка делает эквивалентность правил Вудворда–Хоффмана анализу Дьюара–Циммермана (см. ниже) очевидной. Четное общее число инверсий фаз эквивалентно четному числу антарафациальных компонентов и соответствует топологии Хюккеля, требующей 4 n + 2 электронов для ароматичности, в то время как нечетное общее число инверсий фаз эквивалентно нечетному числу антарафациальных компонентов и соответствует топологии Мёбиуса, требующей 4 n электронов для ароматичности. ^[24] Подводя итог теории ароматических переходных состояний: Термические перициклические реакции протекают через (4 n + 2) -электронные переходные состояния Хюккеля или (4 n ) -электронные переходные состояния Мёбиуса .

В качестве мнемонического приема приведенную выше формулу можно перефразировать следующим образом:

Перициклический процесс в основном состоянии с участием N электронных пар и A антарафациальных компонентов является симметрийно разрешенным тогда и только тогда, когда N + A нечетно.

Альтернативное доказательство эквивалентности

Эквивалентность двух формулировок можно также увидеть с помощью простого аргумента о четности, не прибегая к анализу случаев.

Предложение. Следующие формулировки правил Вудворда–Хоффмана эквивалентны:

(A) Для перициклической реакции, если сумма числа супрафациальных 4q + 2 компонентов и антарафациальных 4r компонентов нечетна, то она термически разрешена; в противном случае реакция термически запрещена.

(B) Для перициклической реакции, если общее число антарафациальных компонентов (4n + 2)-электронной реакции четно или общее число антарафациальных компонентов 4n-электронной реакции нечетно, то она термически разрешена; в противном случае реакция термически запрещена.

Доказательство эквивалентности: индексируем компоненты k -компонентной перициклической реакциии присваиваем компоненту i символ Вудворда-Хоффмана _σ/π/ω N _s/a, число электронов и символ топологической четностив соответствии со следующими правилами: ${\displaystyle i=1,2,\ldots ,k}$ ${\displaystyle (n_{i},p_{i},i)}$

${\displaystyle n_{i}={\begin{cases}0,&N\equiv 0\ (\mathrm {mod} \ 4)\\1,&N\equiv 2\ (\mathrm {mod} \ 4)\end{cases}}\quad \mathrm {and} \quad p_{i}={\begin{cases}0,&i{\text{ is supra}}\\1,&i{\text{ is antara}}\end{cases}}.}$

У нас есть математически эквивалентная переформулировка (A) :

(A') Набор символов ${\displaystyle \{(n_{i},p_{i},i)\}}$ термически допустим тогда и только тогда, когда число символов с этим свойством нечетно. ${\displaystyle n_{i}\neq p_{i}}$

Поскольку общее число электронов равно 4 n + 2 или 4 n именно тогда, когда (число (4 q + 2)-электронных компонентов) нечетное или четное, соответственно, в то время как дает число антарафациальных компонентов, мы также можем переформулировать (B) : ${\textstyle \sum _{i}n_{i}}$ ${\textstyle \sum _{i}p_{i}}$

(B') Набор символов термически допустим тогда и только тогда, когда ровно один из ${\displaystyle \{(n_{i},p_{i},i)\}}$ или является нечетным. ${\textstyle \sum _{i}n_{i}}$ ${\textstyle \sum _{i}p_{i}}$

Достаточно показать, что (A') и (B') эквивалентны. Точно один из или является нечетным тогда и только тогда, когда является нечетным. Если , выполняется; следовательно, исключение символов со свойством из коллекции не изменит четность . С другой стороны, когда , мы имеем , но просто перечисляет количество компонентов со свойством . Следовательно, ${\textstyle \sum _{i}n_{i}}$ ${\textstyle \sum _{i}p_{i}}$ ${\textstyle \sum _{i}n_{i}+\sum _{i}p_{i}=\sum _{i}n_{i}+p_{i}}$ ${\displaystyle n_{i}=p_{i}}$ ${\displaystyle n_{i}+p_{i}\equiv 0\ (\mathrm {mod} \ 2)}$ ${\displaystyle n_{i}=p_{i}}$ ${\textstyle \sum _{i}n_{i}+p_{i}}$ ${\displaystyle n_{i}\neq p_{i}}$ ${\displaystyle n_{i}+p_{i}=1}$ ${\textstyle \sum _{n_{i}\neq p_{i}}1}$ ${\displaystyle n_{i}\neq p_{i}}$

${\displaystyle \sum _{i}n_{i}+p_{i}\equiv \sum _{n_{i}\neq p_{i}}n_{i}+p_{i}=\sum _{n_{i}\neq p_{i}}1=\#\{(n_{i},p_{i},i)\ |\ n_{i}\neq p_{i}\}\ (\mathrm {mod} \ 2)}$.

Таким образом, и число символов в коллекции со свойством имеют одинаковую четность. Поскольку формулировки (A') и (B') эквивалентны, то эквивалентны также (A) и (B) , как и утверждается. □ ${\textstyle \sum _{i}n_{i}+p_{i}}$ ${\displaystyle n_{i}\neq p_{i}}$

Чтобы привести конкретный пример, гипотетической реакции с дескриптором [ _π 6 _s + _π 4 _a + _π 2 _a ] будет назначен набор {(1, 0, 1), (0, 1, 2), (1, 1, 3)} в схеме выше. Есть два компонента, (1, 0, 1) и (0, 1, 2), со свойством , поэтому реакция не допускается (A') . Аналогично, и оба четные, поэтому (B') дает тот же вывод (как и должно быть): реакция не допускается. ${\displaystyle n_{i}\neq p_{i}}$ ${\textstyle \sum _{i}n_{i}=2}$ ${\textstyle \sum _{i}p_{i}=2}$

Примеры

Эта формулировка для 2-компонентной реакции эквивалентна правилам отбора для реакций [ p + q ]-циклоприсоединения, показанным в следующей таблице:

Если общее число электронов равно 4 n + 2, то один находится в нижней строке таблицы. Реакция термически разрешена, если она супрафациальна по отношению к обоим компонентам или антарафациальна по отношению к обоим компонентам. То есть число антарафациальных компонентов четное (оно равно 0 или 2). Аналогично, если общее число электронов равно 4 n , то один находится в верхней строке таблицы. Это термически разрешено, если она супрафациальна по отношению к одному компоненту и антарафациальна по отношению к другому. Таким образом, общее число антарафациальных компонентов всегда нечетное, поскольку оно всегда равно 1.

Ниже приведены некоторые общие классы реакций основного состояния (т.е. термические), проанализированные в свете обобщенных правил Вудворда–Хоффмана.

[2+2] Циклоприсоединение

Термически разрешенная супра-антара [2+2]-димеризация напряженного транс- олефина

[2+2]-циклоприсоединение — это 4-электронный процесс, который объединяет два компонента. Таким образом, согласно приведенным выше общим правилам WH, он разрешен только в том случае, если реакция является антарафациальной по отношению ровно к одному компоненту. Это тот же вывод, к которому пришли с помощью корреляционных диаграмм в разделе выше.

Редкий, но стереохимически однозначный пример [ _π 2 _s + _π 2 _a ]-циклоприсоединения показан справа. Напряжение и стерические свойства транс - двойной связи позволяют осуществить этот, как правило, кинетически неблагоприятный процесс. Считается, что цис , транс -1,5-циклооктадиен также подвергается димеризации посредством этого режима. ^[16] Кетены представляют собой большой класс реагентов, благоприятствующих [2 + 2]-циклоприсоединению с олефинами. Анализ МО циклоприсоединения кетена усложняется и становится неоднозначным из-за одновременного, но независимого взаимодействия ортогональных орбиталей кетена, но может также включать взаимодействие [ _π 2 _s + _π 2 _{a ].} ^[25]

[4+2] Циклоприсоединение

Синхронная 6π-электронная реакция Дильса-Альдера представляет собой [ _π 4 _s + _π 2 _s ]-циклоприсоединение (т.е. супрафациальное по отношению к обоим компонентам), как показано на примере реакции справа.

Реакция Дильса-Альдера является супрафациальной по отношению к обоим компонентам.

Таким образом, поскольку общее число антарафациальных компонентов равно 0, что является четным, реакция является разрешенной симметрией. ^[16] Это предсказание согласуется с экспериментом, поскольку реакция Дильса-Альдера является довольно легкой перициклической реакцией.

4нЭлектроциклическая реакция

Электроциклическая реакция раскрытия кольца с 4 n- электронами может рассматриваться как имеющая 2 компонента – π-систему и разрыв σ-связи. По отношению к π-системе реакция является супрафациальной. Однако при конротаторном механизме, как показано на рисунке выше, реакция является антарафациальной по отношению к σ-связи. Наоборот, при дисротаторном механизме она является супрафациальной по отношению к разрыву σ-связи.

Согласно приведенным выше правилам, для 4 n- электронной перициклической реакции из 2 компонентов должен быть один антарафациальный компонент. Таким образом, реакция должна протекать через конротаторный механизм. ^[16] Это согласуется с результатом, полученным в корреляционных диаграммах выше.

4н+ 2 электроциклическая реакция

Электроциклическая реакция раскрытия кольца 4 n + 2 также является 2-компонентной перициклической реакцией, которая является супрафациальной по отношению к π-системе. Таким образом, для того, чтобы реакция была разрешена, число антарафациальных компонентов должно быть равно 0, т.е. она должна быть супрафациальной также по отношению к разрывающейся σ-связи. Таким образом, дисротаторный механизм является симметрийно разрешенным. ^[16]

[1,дж]-сигматропная перегруппировка

Классический пример Берсона (1967) [1,3]-сигматропного алкильного сдвига, происходящего со стереохимической инверсией (символ WH [ _σ 2 _a + _π 2 _s ])

[1, j ]-сигматропная перегруппировка также является двухкомпонентной перициклической реакцией: один компонент — это π-система, другой компонент — мигрирующая группа. Простейшим случаем является [1, j ]-гидридный сдвиг через π-систему, где j нечетно. В этом случае, поскольку водород имеет только сферически симметричную s-орбиталь, реакция должна быть супрафациальной по отношению к водороду. Общее число вовлеченных электронов равно ( j + 1), поскольку в реакции участвуют ( j − 1)/2 π-связи плюс σ-связь. Если j = 4 n − 1, то она должна быть антарафациальной, а если j = 4 n + 1, то она должна быть супрафациальной. ^[16] Это согласуется с экспериментом, согласно которому сдвиги [1,3]-гидрида обычно не наблюдаются, поскольку разрешенный симметрией антарафациальный процесс невозможен, но сдвиги [1,5]-гидрида происходят довольно легко.

Для [1, j ]-алкильного сдвига, где реакция может быть антарафациальной (т.е. инвертировать стереохимию) по отношению к углеродному центру, применяются те же правила. Если j = 4 n − 1, то реакция разрешена по симметрии, если она либо антарафациальна по отношению к π-системе, либо инвертирует стереохимию у углерода. Если j = 4 n + 1, то реакция разрешена по симметрии, если она супрафациальна по отношению к π-системе и сохраняет стереохимию у углеродного центра. ^[16]

Справа представлен один из первых примеров [1,3]-сигматропного сдвига, обнаруженного Берсоном в 1967 году. ^[26] Для того чтобы обеспечить инверсию конфигурации, при разрыве σ-связи фрагмент C(H)(D) закручивается в переходном состоянии, при этом гибридизация углерода приближается к sp2 ^, так что оставшаяся негибридизованная p-орбиталь сохраняет перекрытие с обоими атомами углерода 1 и 3.

Эквивалентность других теоретических моделей

Анализ Дьюара-Циммермана

Гипотетическая ароматичность Хюккеля и Мёбиуса.

Обобщенные правила Вудворда-Хоффмана, впервые данные в 1969 году, эквивалентны более раннему общему подходу, концепции Мёбиуса-Хюккеля Циммермана, которая была впервые сформулирована в 1966 году и также известна как теория ароматического переходного состояния . ^{[3] [27] [28]} В качестве своего центрального принципа теория ароматического переходного состояния утверждает, что «разрешенные» перициклические реакции протекают через переходные состояния с ароматическим характером, в то время как «запрещенные» перициклические реакции столкнулись бы с переходными состояниями, которые являются антиароматическими по своей природе. В анализе Дьюара-Циммермана рассматривается топология переходного состояния перициклической реакции. Если переходное состояние включает 4 n электронов, топология Мёбиуса является ароматической, а топология Хюккеля является антиароматической, в то время как если переходное состояние включает 4 n + 2 электронов, топология Хюккеля является ароматической, а топология Мёбиуса является антиароматической. Четность числа инверсий фаз (подробно описанных ниже) в переходном состоянии определяет его топологию. Топология Мёбиуса включает нечетное число инверсий фаз, тогда как топология Хюккеля включает четное число инверсий фаз.

Примеры анализа Дьюара-Циммермана, применяемого к обычным перициклическим реакциям. (Красные кривые представляют инверсии фаз.)

В связи с терминологией Вудворда–Хоффмана, число антарафациальных компонентов и число инверсий фаз всегда имеют одинаковую четность. ^[24] Следовательно, нечетное число антарафациальных компонентов дает топологию Мёбиуса, в то время как четное число дает топологию Хюккеля. Таким образом, чтобы переформулировать результаты теории ароматического переходного состояния на языке Вудворда и Хоффмана, реакция с 4 n -электронами термически разрешена тогда и только тогда, когда она имеет нечетное число антарафациальных компонентов (т. е. топология Мёбиуса); реакция с (4 n + 2) -электронами термически разрешена тогда и только тогда, когда она имеет четное число антарафациальных компонентов (т. е. топология Хюккеля).

Процедура анализа Дьюара-Циммермана (примеры показаны справа): Шаг 1. Затенение всех базисных орбиталей, которые являются частью перициклической системы. Затенение может быть произвольным. В частности, затенение не обязательно должно отражать фазировку полиеновых МО; каждая базисная орбиталь просто должна иметь две противоположно фазированные доли в случае p- или spx- ^{гибридных} орбиталей или одну фазу в случае s-орбитали. Шаг 2. Нарисуйте связи между долями базисных орбиталей, которые геометрически хорошо расположены для взаимодействия в переходном состоянии. Связи, которые необходимо сделать, зависят от топологии переходного состояния. (Например, на рисунке показаны различные связи в случаях кон- и дисротаторной электроциклизации.) Шаг 3. Подсчитайте количество связей, которые возникают между долями противоположной затененности: каждая из этих связей представляет собой инверсию фазы. Если число инверсий фаз четное, то переходное состояние — Хюккеля, а если число инверсий фаз нечетное, то переходное состояние — Мёбиуса. Шаг 4. Сделайте вывод, что перициклическая реакция разрешена, если число электронов равно 4 n + 2 и переходное состояние — Хюккеля, или если число электронов равно 4 n и переходное состояние — Мёбиуса; в противном случае сделайте вывод, что перициклическая реакция запрещена.

Важно отметить, что приемлема любая схема присвоения относительных фаз базисным орбиталям, поскольку инвертирование фазы любой отдельной орбитали добавляет 0 или ±2 инверсии фазы к общему числу, т.е. четное число, так что четность числа инверсий (число инверсий по модулю 2) остается неизменной.

Переосмысление с помощью концептуальной теории функционала плотности

Недавно правила Вудворда-Хоффмана были переосмыслены с использованием концептуальной теории функционала плотности (DFT). ^{[29] [30]} Ключом к анализу является функция двойного дескриптора, предложенная Кристофом Мореллем, Андре Грандом и Алехандро Торо-Лаббе ^[31] , вторая производная электронной плотности по числу электронов . Эта функция отклика важна, поскольку реакция двух компонентов A и B, включающая передачу электронов, будет зависеть от восприимчивости электронной плотности к отдаче или принятию электронов, т.е. производной функции Фукуи . Фактически, с упрощенной точки зрения, функция двойного дескриптора дает показания об электрофильности или нуклеофильности различных областей молекулы. Для область является электрофильной, а для область является нуклеофильной. Используя предположение о граничной молекулярной орбитали и конечно-разностное приближение функции Фукуи, можно записать функцию двойного дескриптора как ${\displaystyle f^{(2)}(r)={\frac {\partial ^{2}\rho (r)}{\partial N^{2}}}}$ ${\displaystyle \rho (r)}$ ${\displaystyle N}$ ${\displaystyle f(r)={\frac {\partial \rho (r)}{\partial N}}}$ ${\displaystyle f^{(2)}>0}$ ${\displaystyle f^{(2)}<0}$

${\displaystyle f^{(2)}(r)={\frac {\partial f(r)}{\partial N}}\cong |\phi _{\text{LUMO}}(r)|^{2}-|\phi _{\text{HOMO}}(r)|^{2}}$

Это имеет интуитивно понятный смысл, так как если область лучше принимает электроны, чем отдает, то LUMO должен доминировать, а функция двойного дескриптора будет положительной. И наоборот, если область лучше отдает электроны, то термин HOMO будет доминировать, а дескриптор будет отрицательным. Обратите внимание, что хотя концепция фазы и орбиталей заменена просто понятием электронной плотности, эта функция по-прежнему принимает как положительные, так и отрицательные значения.

Двойная окраска (красный>0, синий<0) электронной плотности в состоянии супра/супра перехода Дильса-Альдера.

Правила Вудворда–Хоффмана переосмысливаются с использованием этой формулировки путем сопоставления благоприятных взаимодействий между областями электронной плотности, для которых дуальный дескриптор имеет противоположные знаки. Это эквивалентно максимизации предсказанных благоприятных взаимодействий и минимизации отталкивающих взаимодействий. Для случая циклоприсоединения [4+2] упрощенная схема реагентов с функцией дуального дескриптора, окрашенной (красный = положительный, синий = отрицательный), показана в оптимальной конфигурации supra/supra слева. Этот метод правильно предсказывает правила WH для основных классов перициклических реакций.

Исключения

В главе 12 « Закона о сохранении орбитальной симметрии », озаглавленной «Нарушения», Вудворд и Хоффманн заявили:

Нет их! И нельзя ожидать нарушений столь основополагающего принципа максимальной связи.

Несмотря на это заявление, важно признать, что правила Вудворда-Хоффмана используются для прогнозирования относительной высоты барьера и, таким образом, вероятных механизмов реакции, и что они учитывают только барьеры, обусловленные сохранением орбитальной симметрии. Таким образом, не гарантируется, что реакция, разрешенная симметрией WH, действительно происходит легко. Наоборот, при достаточном энергетическом вложении возможно получение продукта анти-Вудворда-Хоффмана. Это особенно распространено в стерически ограниченных системах, где продукт WH имеет дополнительный стерический барьер для преодоления. Например, в электроциклическом раскрытии кольца производного диметилбицикло[0.2.3]гептена ( 1 ) конротаторный механизм невозможен из-за результирующей угловой деформации, и реакция медленно протекает через дисротаторный механизм при 400 ^o C, давая продукт циклогептадиен. ^[2] Нарушения могут также наблюдаться в случаях с очень сильными термодинамическими движущими силами. Разложение диоксетан-1,2-диона на две молекулы углекислого газа, известного своей ролью в люминесценции светящихся палочек , было тщательно изучено вычислительно. В отсутствие флуоресцентов реакция, как теперь полагают, протекает согласованным (хотя и асинхронным) образом, через ретро-[2+2]-циклоприсоединение, которое формально нарушает правила Вудворда-Хоффмана. ^[32]

Продукт анти-WH через дисротационный механизм, вызванный кольцевой деформацией.

Расчетно предсказанные продукты электроциклического раскрытия кольца 4e под термическим, фото- и механическим контролем.

Аналогично, недавняя статья описывает, как механическое напряжение может быть использовано для изменения путей химических реакций, чтобы привести к продуктам, которые, по-видимому, нарушают правила Вудворда-Хоффмана. ^[33] В этой статье они используют ультразвуковое облучение, чтобы вызвать механическое напряжение на полимерах с функциональными связями, присоединенных син или анти к циклобутеновому кольцу. Вычислительные исследования предсказывают, что механическая сила, возникающая в результате трения полимеров, вызывает удлинение связи вдоль координаты реакции конротаторного механизма в анти-бизамещенном-циклобутене и вдоль координаты реакции дисротаторного механизма в син-бизамещенном-циклобутене. Таким образом, в син-бизамещенном-циклобутене, как предсказывают, образуется продукт анти -WH.

Это вычислительное предсказание было подкреплено экспериментом на системе ниже. Связующие функционализированные полимеры были сопряжены с цис -бензоциклобутеном как в син-, так и в анти-конформациях. Как и предсказывалось, оба продукта дали один и тот же продукт (Z,Z), как определено тушением стереоспецифической реакцией Дильса-Альдера с замещенным малеимидом. В частности, син-замещенный продукт дал анти-WH продукт, предположительно, поскольку механическое растяжение вдоль координаты дисротационного пути снизило барьер реакции под дисротационным путем достаточно, чтобы сместить этот механизм.

Противоречие

Было заявлено, что Элиас Джеймс Кори , также лауреат Нобелевской премии, чувствует себя ответственным за идеи, которые легли в основу этого исследования, и что Вудворд несправедливо пренебрег признанием его заслуг в открытии. В мемуарах 2004 года, опубликованных в журнале Journal of Organic Chemistry , ^[34] Кори заявляет о своем приоритете идеи: «4 мая 1964 года я предложил своему коллеге Р. Б. Вудворду простое объяснение, включающее симметрию возмущенных (HOMO) молекулярных орбиталей для стереоселективных превращений циклобутена в 1,3-бутадиен и 1,3,5-гексатриена в циклогексадиен, что послужило основой для дальнейшего развития этих идей в то, что стало известно как правила Вудворда–Хоффмана».

Кори, которому тогда было 35 лет, работал до вечера в понедельник, 4 мая, как он и другие увлеченные химики часто делали. Около 8:30 вечера он зашел в офис Вудворда, и Вудворд задал вопрос о том, как предсказать тип кольца, которое сформирует цепочка атомов. После некоторого обсуждения Кори предположил, что конфигурация электронов управляет ходом реакции. Вудворд настаивал, что решение не сработает, но Кори оставил чертежи в офисе, уверенный, что он что-то нащупал. ^[35]

«Я чувствовал, что это будет действительно интересным развитием событий, и с нетерпением ждал какого-то совместного предприятия», — написал он. Но на следующий день Вудворд влетел в офис Кори, когда тот и его коллега уходили на обед, и представил идею Кори как свою собственную — и затем ушел. Кори был ошеломлен.

В опровержении 2004 года, опубликованном в Angewandte Chemie , ^[36] Роальд Хоффманн опроверг это утверждение: он цитирует Вудворда из лекции, прочитанной в 1966 году, в которой он говорит: «Я ПОМНЮ очень ясно — и это все еще несколько удивляет меня, — что решающая вспышка просветления пришла ко мне в алгебраической, а не в графической или геометрической форме. Совершенно неожиданно мне пришло в голову, что коэффициенты терминальных членов в математическом выражении, представляющем наивысшую занятую молекулярную орбиталь бутадиена, имеют противоположные знаки, в то время как коэффициенты соответствующего выражения для гексатриена имеют тот же знак. Отсюда был всего лишь короткий шаг к геометрическому и, что более очевидно, химически релевантному взгляду, что при внутренней циклизации диена верхняя грань одного терминального атома должна атаковать нижнюю грань другого, тогда как в случае триена образование новой связи должно включать верхние (или pari passu, нижние) грани обоих терминальных атомов».

Кроме того, Хоффманн указывает, что в двух публикациях 1963 ^[37] и 1965 ^[38] Кори описал полный синтез соединения дигидрокостунолида. Хотя они описывают электроциклическую реакцию, Кори ничего не может предложить относительно объяснения стереоспецифичности синтеза.

Эта фотохимическая реакция с участием 6 = 4×1 + 2 электронов теперь считается конротаторной.

Смотрите также

• Правила Вудворда для расчета поглощения УФ-излучения
• Торкоселективность

Примечания

Ссылки

1. Принцип сохранения орбитальной симметрии обычно приписывают Роберту Бернсу Вудворду и Роальду Хоффманну , которые предложили сохранение орбитальной симметрии в качестве объяснения стереохимического результата электроциклических реакций ( J. Am. Chem. Soc. 1965 , 87 , 395) и несколько лет спустя сформулировали полностью обобщенное перициклическое правило отбора ( Angew. Chem. Int. Ed. Engl. 1969 , 8 , 781). Однако Э. Дж. Кори заявил о приоритете в предложении ключевого понимания в 1965 году ( см. раздел «Противоречие» ниже ). Более того, Э. Хавинга ранее отмечал, что тахистерол подвергается электроциклическому замыканию кольца конротаторным или дисротаторным образом в зависимости от режима активации (фотохимического или термического соответственно) и приписал объяснение этого явления с помощью орбитальной симметрии Л. Дж. Остерхоффу ( Tetrahedron Lett. 1961 , 16 , 146). Кроме того, теория переходного состояния ароматических соединений , выдвинутая Х. Э. Циммерманом ( J. Am. Chem. Soc. 1966 , 88 , 1564) и М. Дж. С. Дьюаром ( Tetrahedron 1966 , Suppl. 8 , 75), была признана альтернативным подходом, который полностью эквивалентен формулировке обобщенного правила Вудворда и Хоффмана, но предшествует ей.
2. Вудворд, Р. Б.; Хоффманн, Роальд (1965). «Стереохимия электроциклических реакций». Журнал Американского химического общества . 87 (2): 395. doi :10.1021/ja01080a054.
3. Zimmerman, HE (1966). «О диаграммах корреляции молекулярных орбиталей, появлении систем Мёбиуса в реакциях циклизации и факторах, контролирующих реакции в основном и возбужденном состоянии. I». Журнал Американского химического общества . 88 (7): 1564–1565. doi :10.1021/ja00959a052.
4. Циммерман, Говард Э. (1971-08-01). «Концепция Мебиуса-Хюккеля в органической химии. Применение органических молекул и реакций». Accounts of Chemical Research . 4 (8): 272–280. doi :10.1021/ar50044a002. ISSN  0001-4842.
5. Dewar, MJS (1966-01-01). «Теория молекулярных орбиталей органической химии — VIII: романтизм и электроциклические реакции». Tetrahedron . 22 : 75–92. doi :10.1016/S0040-4020(01)82171-2. ISSN  0040-4020.
6. Dewar, Michael JS (1971-11-01). «Ароматичности и перициклические реакции». Angewandte Chemie International Edition на английском языке . 10 (11): 761–776. doi :10.1002/anie.197107611. ISSN  1521-3773.
7. Фукуи, Кенити (1965-01-01). «Стереоселективность, связанная с нециклоприсоединением к ненасыщенным связям». Tetrahedron Letters . 6 (28): 2427–2432. doi :10.1016/S0040-4039(00)90203-X. ISSN  0040-4039.
8. Фукуи, Кенити (1982). «Роль граничных орбиталей в химических реакциях». Science . 218 (4574): 747–754. Bibcode :1982Sci...218..747F. doi :10.1126/science.218.4574.747. JSTOR  1689733. PMID  17771019.
9. Geerlings, Paul; Ayers, Paul W.; Toro-Labbé, Alejandro; Chattaraj, Pratim K.; De Proft, Frank (2012). «Правила Вудворда–Хоффмана, переосмысленные концептуальной теорией функционала плотности». Accounts of Chemical Research . 45 (5): 683–95. doi :10.1021/ar200192t. hdl : 10533/131820 . PMID  22283422.
10. Нобелевская премия по химии 1981 года. Nobelprize.org.
11. Криджи, Рудольф; Нолл, Клаус (1959). «Umsetzungen in der Reihe des 1.2.3.4-тетраметилциклобутаны». Юстус Либигс Аннален дер Хими . 627 : 1–14. дои : 10.1002/jlac.19596270102.
12. Хотя на рисунке ниже оба конца показаны вращающимися по часовой стрелке, важно понимать, что орбитальная симметрия различает только вращение в одном направлении или в противоположных направлениях ( конротация против дисротации ). Образование изомера ( Z , Z ) из раскрытия кольца 1 (оба конца вращаются против часовой стрелки) также является симметрией, разрешенной. То, что изомер ( Z , Z ) не наблюдался, вероятно, связано с неблагоприятными стерическими взаимодействиями между вращающимися внутрь метильными группами. (В других случаях предпочтение вращения связи по часовой стрелке или против часовой стрелки может контролироваться стереоэлектронными факторами: см. торквоселективность .)
13. Шринивасан, Р. (1968-07-01). «Механизм фотохимической валентной таутомеризации 1,3-бутадиенов». Журнал Американского химического общества . 90 (16): 4498–4499. doi :10.1021/ja01018a080. ISSN  0002-7863.
14. Винтер, Рудольф Эрнст К. (1965-01-01). «Получение и изомеризация цис- и транс-3,4-диметилциклобутена». Tetrahedron Letters . 6 (17): 1207–1212. doi :10.1016/S0040-4039(01)83997-6. ​​ISSN  0040-4039.
15. Исходное утверждение, данное Вудвордом и Хоффманном, несколько более подробно: Перициклическое изменение основного состояния является симметрией разрешенным, когда общее число компонентов (4q+2) _s и (4r) _a нечетно. Однако утверждение, данное здесь, математически эквивалентно. Доказательство см.: https://archive.org/details/whdz_red
16. Вудворд, Р. Б.; Хоффманн, Роальд (1969). «Сохранение орбитальной симметрии». Angew. Chem. Int. Ed . 8 (11): 781–853. doi :10.1002/anie.196907811.
17. Лонге-Хиггинс, HC; Абрахамсон, EW (1965). «Электронный механизм электроциклических реакций». Журнал Американского химического общества . 87 (9): 2045. doi :10.1021/ja01087a033.
18. Вудворд, Р. Б.; Хоффманн, Роальд (1971). Сохранение орбитальной симметрии (3-е издание, 1-е изд.). Вайнхайм, BRD: Verlag Chemie GmbH (BRD) и Academic Press (США). стр. 1–178. ISBN 978-1483256153.
19. PR Bunker и P. Jensen (2005), Основы молекулярной симметрии (CRC Press) ISBN 0-7503-0941-5 [1] см. раздел 10.4 
20. Кэрролл, Феликс (1998) Перспективы структуры и механизма в органической химии , Brooks/Cole, стр. 710–794, ISBN 0534249485 . 
21. Точнее, «симметрически-запрещенная» система с истинной симметрией имеет исходные материальные связывающие орбитали, которые коррелируют с продуктом антисвязывающих орбиталей и наоборот. Напротив, когда заместитель нарушает симметрию, эти пересечения уровней «едва избегаются» энергетическими уровнями, которые приближаются (вблизи переходного состояния), но затем расходятся. В отличие от разницы в диаграммах орбитальной корреляции, диаграммы корреляции состояний всегда имеют «едва избегаемые» пересечения, независимо от того, является ли симметрия «истинной» или «приблизительной». Таким образом, наличие или отсутствие простого заместителя, который нарушает формальный элемент симметрии, несущественно, поскольку диаграмма корреляции состояний не меняется в качественном смысле. Рост энергии основного состояния по мере приближения к «едва избегаемому» пересечению приводит к налагаемому симметрией энергетическому барьеру в переходном состоянии.
22. Хоффманн, Роальд; Вудворд, РБ (1965). «Правила отбора для реакций согласованного циклоприсоединения». J. Am. Chem. Soc . 87 (9): 2046. doi :10.1021/ja01087a034.
23. Поскольку SO ₂ имеет ортогональную неподеленную пару и антисвязывающие орбитали (аллил-подобная антисвязывающая орбиталь SO ₂ анализируется здесь как простая незанятая p-орбиталь), взаимодействие этих орбиталей с орбиталями 1,3-бутадиена должно анализироваться отдельно. В общем случае для составного процесса, такого как эта хелетропная реакция, оба отдельных орбитальных взаимодействия должны быть разрешены для того, чтобы реакция была разрешена. Подход FMO, вероятно, дает здесь наиболее интуитивную картину.
24. Возможно выполнить анализ Дьюара-Циммермана с максимум одной инверсией фазы, и что результат зависит от четности числа антарафациальных компонентов. Процесс включает в себя затенение первой орбитали любого компонента произвольно и завершение затенения остальной части компонента так, чтобы внутри него не произошло инверсии фазы. Между компонентами рисуются связи Дьюара-Циммермана на основе топологии связи ( супра или антара ) каждого компонента. Используя эти связи, можно продолжить затенение на соседние компоненты так, чтобы между компонентами или внутри компонента не было инверсии. Это продолжается до тех пор, пока все взаимодействующие орбитали не будут затенены, и для завершения цикла потребуется только сделать последнюю связь Дьюара-Циммермана. До этого момента инверсия фазы не была введена. Важное наблюдение: связи Дьюара-Циммермана, простирающиеся от двух концов антарафациального (супрафациального) компонента к соседним компонентам, соединят доли противоположного (того же) затенения . Следовательно, нечетное число антарафациальных компонентов вызовет одну инверсию фазы для завершения цикла, в то время как четное число антарафациальных компонентов позволит завершить цикл без инверсии фазы. Поскольку число инверсий (по модулю 2) инвариантно относительно фазирования орбит, эти две возможности (нечетное или четное число антарафациальных компонентов) фиксируют, применяется ли система Мёбиуса (одна инверсия) или Хюккеля (нет инверсии) соответственно.
25. Ямабэ, Шиничи; Кувата, Каёко; Минато, Цутому (1999). «Frontier-orbital analyses of ketene [2+2] cycloadditions». Theoretical Chemistry Accounts: Theory, Computation, and Modeling . 102 (1–6): 139–146. doi :10.1007/s002140050484. S2CID  206899145.
26. Берсон, Джером А.; Нельсон, Джордж Л. (1967-10-01). «Инверсия конфигурации в мигрирующей группе тепловой 1,3-сигматропной перегруппировки». Журнал Американского химического общества . 89 (21): 5503–5504. doi :10.1021/ja00997a065. ISSN  0002-7863.
27. Циммерман, Х. Э. (1966). «О диаграммах корреляции молекулярных орбиталей, системах Мёбиуса и факторах, контролирующих реакции в основном и возбужденном состоянии. II». J. Am. Chem. Soc . 88 (7): 1566–156. doi :10.1021/ja00959a053.
28. Циммерман, Х. Э. (2006). «Пять десятилетий механистической и исследовательской органической фотохимии». Pure Appl. Chem . 78 (12): 2193–2203. doi : 10.1351/pac200678122193 . S2CID  37436155.
29. Geerlings, Paul; Ayers, Paul W.; Toro-Labbé, Alejandro; Chattaraj, Pratim K.; De Proft, Frank (2012). «Правила Вудворда–Хоффмана, переосмысленные концептуальной теорией функционала плотности». Accounts of Chemical Research . 45 (5): 683–95. doi :10.1021/ar200192t. hdl : 10533/131820 . PMID  22283422.
30. Ayers, Paul W.; Morell, Christophe; De Proft, Frank; Geerlings, Paul (5 октября 2007 г.). «Понимание правил Вудворда–Хоффмана с помощью изменений электронной плотности». Chemistry: A European Journal . 13 (29): 8240–8247. doi :10.1002/chem.200700365. PMID  17639522.
31. Morell, Christophe; Grand, André; Toro-Labbé, Alejandro (1 января 2005 г.). «Новый двойной дескриптор химической реактивности». The Journal of Physical Chemistry A . 109 (1): 205–212. Bibcode :2005JPCA..109..205M. doi :10.1021/jp046577a. hdl : 10533/176692 . PMID  16839107.
32. Фарахани, Пурия; Баадер, Вильгельм Дж. (2017-02-16). «Механизм мономолекулярного разложения 1,2-диоксетандиона: согласованный или бирадикальный? Вот в чем вопрос!». Журнал физической химии A. 121 ( 6): 1189–1194. Bibcode : 2017JPCA..121.1189F. doi : 10.1021/acs.jpca.6b10365. ISSN  1089-5639. PMID  28094939.
33. Хикенбот, Чарльз Р.; Мур, Джеффри С.; Уайт, Скотт Р.; Соттос, Нэнси Р.; Бодри, Джером; Уилсон, Скотт Р. (2007). «Смещение путей реакции с помощью механической силы». Nature . 446 (7134): 423–7. Bibcode :2007Natur.446..423H. doi :10.1038/nature05681. PMID  17377579. S2CID  4427747.
34. Corey, EJ (2004). «Невозможные мечты». Журнал органической химии . 69 (9): 2917–9. doi :10.1021/jo049925d. PMID  15104426.
35. Джонсон, Кэролин И. (1 марта 2005 г.) Чья это была идея? Boston Globe
36. Хоффманн, Роальд (2004). «Заявление о развитии пограничного орбитального объяснения электроциклических реакций». Angewandte Chemie International Edition . 43 (48): 6586–90. doi : 10.1002/anie.200461440 . PMID  15558636.
37. Кори, Э. Дж.; Хортманн, Альфред Г. (1963). «Полный синтез дигидрокостунолида». Журнал Американского химического общества . 85 (24): 4033. doi :10.1021/ja00907a030.
38. Corey, EJ; Hortmann, Alfred G. (1965). «Полный синтез дигидрокостунолида». Журнал Американского химического общества . 87 (24): 5736–42. doi :10.1021/ja00952a037. PMID  5845424.

Журнальные статьи

• Понимание правил Вудворда-Хоффмана с использованием изменений электронной плотности ^[1]

1. Ayers, Paul W.; Morell, Christophe; De Proft, Frank; Geerlings, Paul (5 октября 2007 г.). «Понимание правил Вудворда–Хоффмана с помощью изменений электронной плотности». Chemistry: A European Journal . 13 (29): 8240–8247. doi :10.1002/chem.200700365. PMID  17639522.