Спица — один из стержней, исходящих из центра колеса ( ступицы , к которой крепится ось ) и соединяющих ступицу с круглой поверхностью тяги.





Первоначально этот термин относился к частям бревна, которые были расколоты (расколоты по длине) на четыре или шесть частей. Радиальные элементы колеса фургона изготавливались путем вырезания спицы (из бревна) в их готовой форме. Стружка для спицы — это инструмент , изначально разработанный для этой цели. В конечном итоге термин спица стал чаще применяться к готовому продукту работы колесника , чем к материалам, которые они использовали.
Колесо со спицами было изобретено для того, чтобы можно было строить более легкие и быстрые транспортные средства. Самые ранние физические свидетельства существования колес со спицами были найдены в культуре Синташта , датируемой примерно 2000 г. до н. э. [1] Вскоре после этого конные культуры Кавказского региона использовали конные боевые колесницы со спицами в течение большей части трех столетий. Они продвинулись вглубь Греческого полуострова , где объединились с существующими средиземноморскими народами, чтобы в конечном итоге дать начало классической Греции после разрушения минойского господства и консолидации во главе с доклассической Спартой и Афинами .
Нео- халколитический /протоисторический период (1800-1200 гг. до н.э.) [примечание 1] на картинах в различных регионах Индии, таких как Чиббар Нулла, Чхатур Бходж Нат Нулла, Катхотия и т.д., изображено использование колесниц со спицами на колесах. [5] [6]
Кельтские колесницы ввели железный обод вокруг колеса в 1-м тысячелетии до н. э. Колесо со спицами использовалось без серьезных изменений до 1870-х годов, когда были изобретены проволочные колеса и резиновые шины . [7]
Спицы могут быть изготовлены из дерева, металла или синтетического волокна в зависимости от того, будут ли они подвергаться растяжению или сжатию .
Первоначальный тип колеса со спицами из дерева использовался для конных экипажей и повозок . В ранних автомобилях обычно использовались деревянные колеса со спицами артиллерийского типа.
В простом деревянном колесе нагрузка на ступицу заставляет обод колеса слегка прижиматься к земле, поскольку самая нижняя деревянная спица укорачивается и сжимается. Другие деревянные спицы не показывают существенных изменений.
Деревянные спицы установлены радиально . Они также имеют вогнутую форму, обычно снаружи транспортного средства, чтобы предотвратить виляние. Кроме того, вогнутость позволяет колесу компенсировать расширение спиц из-за поглощенной влаги, выгибаясь больше. [8]
Для использования в велосипедах тяжелые деревянные спицы были заменены более легкими колесами со спицами из натянутой, регулируемой металлической проволоки, называемыми проволочными колесами . Они также использовались в инвалидных колясках , мотоциклах , автомобилях и ранних самолетах .
Некоторые типы колес имеют съемные спицы, которые можно заменить по отдельности, если они сломаются или погнутся. К ним относятся колеса велосипедов и инвалидных колясок. Высококачественные велосипеды с обычными колесами используют спицы из нержавеющей стали , в то время как более дешевые велосипеды могут использовать оцинкованные (также называемые «нержавеющими») или хромированные спицы. Хотя спица хорошего качества способна выдерживать около 225 кгс (около 500 фунтов силы или 2200 ньютонов ) натяжения, они используются при меньшей нагрузке, чтобы избежать усталостных отказов. Поскольку спицы колес велосипедов и инвалидных колясок находятся только в состоянии растяжения, иногда также используются гибкие и прочные материалы, такие как синтетические волокна. [9] Металлические спицы также могут быть овальными или лопастными, чтобы уменьшить аэродинамическое сопротивление, и стыкованными (двойными или даже тройными), чтобы уменьшить вес, сохраняя прочность.
Разновидностью колеса с проволочными спицами был «Tension Disk» от Tioga, который внешне казался сплошным диском, но на самом деле был сконструирован с использованием тех же принципов, что и обычное колесо с проволочными спицами. Вместо отдельных проволочных спиц для шнуровки ступицы с ободом под высоким натяжением использовалась непрерывная нить из кевлара ( арамида ). Нити были заключены в полупрозрачный диск для защиты и некоторого аэродинамического преимущества, но это не было структурным компонентом.
Проволочные спицы могут быть радиальными по отношению к ступице, но чаще всего устанавливаются по касательной к ступице. Тангенциальное расположение спиц позволяет передавать крутящий момент между ободом и ступицей. Таким образом, тангенциальные спицы необходимы для ведущего колеса, которое имеет крутящий момент на ступице от педалирования, и любых колес, использующих тормоза, монтируемые на ступице, такие как дисковые или ленточные тормоза, которые передают крутящий момент от обода к тормозу в противоположном направлении — (через ступицу) при торможении.
Изготовление колеса с натяжными спицами из его составных частей называется сборкой колес и требует правильной процедуры сборки для прочного и долговечного конечного продукта. Натянутые спицы обычно крепятся к ободу или иногда к ступице с помощью ниппеля спицы . Другой конец обычно проковывается в диск или, что необычно, сгибается в «Z», чтобы не дать ему вытянуться через отверстие в ступице. Преимущество изогнутой версии в том, что она заменяет сломанную спицу в заднем колесе велосипеда без необходимости снимать задние шестерни .
Проволочные колеса, с их отличным соотношением веса к прочности, вскоре стали популярными для легковых автомобилей. Для повседневных автомобилей проволочные колеса вскоре были заменены менее дорогими металлическими дисковыми колесами, но проволочные колеса оставались популярными для спортивных автомобилей вплоть до 1960-х годов. Спицованные колеса по-прежнему популярны на мотоциклах и велосипедах .
При сборке велосипедного колеса спицы должны иметь правильную длину, в противном случае может быть недостаточно нитей, что ослабит колесо, или спицы могут выступать через обод и, возможно, проколоть внутреннюю камеру.
Для велосипедных спиц длина спицы определяется от фланцевого гнезда до кончика резьбы. Для спиц с загнутыми концами номинальная длина спицы не включает ширину спицы на загнутом конце.
Для колес с перекрещенными спицами (что является нормой) желаемая длина спиц составляет
где
Относительно d : Для симметричного колеса, например, переднего колеса без дискового тормоза, это половина расстояния между фланцами. Для асимметричного колеса, например, переднего колеса с дисковым тормозом или заднего колеса с цепным переключателем , значение d отличается для левой и правой сторон.
a — угол между (1) радиусом отверстия ниппеля в ободе, к которому прикреплена спица, и (2) радиусом отверстия фланца, удерживающего спицу. Спица пересекает 1, 2 или 3 противоположно направленные спицы в зависимости от конструкции спицовки. На фланце угол между радиусами соседних отверстий составляет 360°/ м (для равномерно расположенных отверстий). Для каждого пересечения спицы ступица поворачивается относительно обода на один «угол между соседними отверстиями фланца». Таким образом, умножение «угла между соседними отверстиями фланца» на k дает угол a . Например, колесо с 32 спицами имеет 16 спиц на сторону, 360°, деленные на 16, равны 22,5°. Умножьте 22,5° («угол между соседними отверстиями фланца») на количество пересечений, чтобы получить угол a — если 3-перекрестия, колесо с 32 спицами имеет угол a, равный 67,5°. Относительно r 3 : Размер отверстий для спиц во фланце не имеет значения для необходимой длины спицы. Этот термин устраняет влияние размера отверстия. Поскольку отверстия обычно небольшие (чуть больше 2 мм в диаметре), эффект невелик и на практике не имеет большого значения.
Для колес с радиальными спицами (нулевые пересечения) формула упрощается до теоремы Пифагора , где длина спицы l плюс r 3 — наклон, r 2 минус r 1 — основание, а d — подъем:
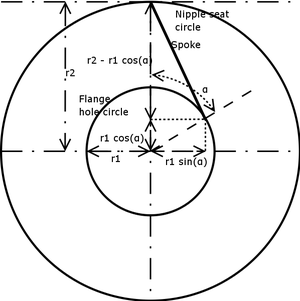
Формула длины спицы вычисляет длину диагонали пространства воображаемого прямоугольного ящика . Представьте, что вы держите колесо перед собой так, что ниппель находится наверху. Посмотрите на колесо вдоль оси. Спица через верхнее отверстие теперь является диагональю воображаемого ящика. Ящик имеет глубину d , высоту r 2 - r 1 cos( α ) и ширину r 1 sin( a ).
Аналогично, закон косинусов можно использовать для того, чтобы сначала вычислить длину спицы, спроецированную на плоскость колеса (как показано на схеме), а затем применить теорему Пифагора .