Статистика заказов

K-е наименьшее значение в статистической выборке

Функции плотности вероятности статистики порядка для выборки объемом n  = 5 из экспоненциального распределения с параметром единичного масштаба

В статистике статистика k -го порядка статистической выборки равна ее k -му наименьшему значению. ^[1] Вместе со статистикой рангов статистика порядков является одним из наиболее фундаментальных инструментов непараметрической статистики и вывода .

Важными особыми случаями порядковой статистики являются минимальное и максимальное значение выборки, а также (с некоторыми оговорками, обсуждаемыми ниже) медиана выборки и другие квантили выборки .

При использовании теории вероятностей для анализа статистики порядка случайных выборок из непрерывного распределения используется кумулятивная функция распределения , чтобы свести анализ к случаю статистики порядка равномерного распределения .

Обозначения и примеры

Например, предположим, что наблюдаются или записываются четыре числа, в результате чего получается выборка размером 4. Если значения выборки равны

6, 9, 3, 8,

статистика заказов будет обозначаться

${\displaystyle x_{(1)}=3,\ \ x_{(2)}=6,\ \ x_{(3)}=8,\ \ x_{(4)}=9,\,}$

где индекс ( i ) , заключенный в круглые скобки, указывает статистику i-го порядка выборки.

Статистика первого порядка (или статистика наименьшего порядка ) всегда является минимумом выборки, то есть

${\displaystyle X_{(1)}=\min\{\,X_{1},\ldots ,X_{n}\,\}}$

где, следуя общепринятому соглашению, мы используем прописные буквы для обозначения случайных величин и строчные буквы (как указано выше) для обозначения их фактических наблюдаемых значений.

Аналогично, для выборки размера n статистика n - го порядка (или статистика наибольшего порядка ) является максимальной , то есть

${\displaystyle X_{(n)}=\max\{\,X_{1},\ldots ,X_{n}\,\}.}$

Диапазон выборки — это разница между максимальным и минимальным значением. Это функция статистики заказов:

${\displaystyle {\rm {Range}}\{\,X_{1},\ldots ,X_{n}\,\}=X_{(n)}-X_{(1)}.}$

Аналогичная важная статистика в исследовательском анализе данных , которая просто связана со статистикой порядка, — это выборочный межквартильный размах .

Выборочная медиана может быть или не быть порядковой статистикой, поскольку единственное среднее значение существует только тогда, когда число n наблюдений нечетно . Точнее, если n = 2 m +1 для некоторого целого числа m , то выборочная медиана является порядковой статистикой. С другой стороны, когда n четно , n = 2 m и имеются два средних значения и , а медиана выборки является некоторой функцией от этих двух (обычно среднего) и, следовательно, не является порядковой статистикой. Подобные замечания применимы ко всем квантилям выборки. ${\displaystyle X_{(m+1)}}$ ${\displaystyle X_{(m)}}$ ${\displaystyle X_{(m+1)}}$

Вероятностный анализ

Учитывая любые случайные величины X ₁ , X ₂ ..., X _n , статистика порядка X ₍₁₎ , X ₍₂₎ , ..., X _{( n )} также является случайными величинами, определяемыми путем сортировки значений ( реализаций ) X 1 , ..., _X n _в порядке возрастания.

Когда случайные величины X ₁ , X ₂ ..., X _n образуют выборку , они независимы и одинаково распределены . Именно этот случай рассматривается ниже. В общем, случайные величины X ₁ , ..., X _n могут возникнуть в результате выборки из более чем одной совокупности. Тогда они независимы , но не обязательно одинаково распределены, а их совместное распределение вероятностей задается теоремой Бапата-Бега .

В дальнейшем мы будем считать, что рассматриваемые случайные величины непрерывны , а там, где это удобно, будем также предполагать, что они имеют функцию плотности вероятности (PDF), то есть абсолютно непрерывны . В конце обсуждаются особенности анализа распределений, присваивающих массу точкам (в частности, дискретных распределений ).

Кумулятивная функция распределения статистики заказов

Для случайной выборки, как указано выше, с кумулятивным распределением , статистика порядка для этой выборки имеет кумулятивное распределение следующим образом ^[2] (где r указывает, какая статистика порядка): ${\displaystyle F_{X}(x)}$

${\displaystyle F_{X_{(r)}}(x)=\sum _{j=r}^{n}{\binom {n}{j}}[F_{X}(x)]^{j}[1-F_{X}(x)]^{n-j}}$

соответствующая функция плотности вероятности может быть получена из этого результата и оказывается равной

${\displaystyle f_{X_{(r)}}(x)={\frac {n!}{(r-1)!(n-r)!}}f_{X}(x)[F_{X}(x)]^{r-1}[1-F_{X}(x)]^{n-r}.}$

Более того, есть два особых случая, в которых CDF легко вычислить.

${\displaystyle F_{X_{(n)}}(x)=\operatorname {Prob} (\max\{\,X_{1},\ldots ,X_{n}\,\}\leq x)=[F_{X}(x)]^{n}}$

${\displaystyle F_{X_{(1)}}(x)=\operatorname {Prob} (\min\{\,X_{1},\ldots ,X_{n}\,\}\leq x)=1-[1-F_{X}(x)]^{n}}$

Это можно получить путем тщательного рассмотрения вероятностей.

Распределения вероятностей статистики заказов

Статистика заказов, выбранная из равномерного распределения

В этом разделе мы показываем, что порядковая статистика равномерного распределения на единичном интервале имеет маргинальные распределения , принадлежащие семейству бета-распределений . Мы также даем простой метод получения совместного распределения любого количества статистик порядка и, наконец, переводим эти результаты в произвольные непрерывные распределения с помощью cdf .

В этом разделе мы предполагаем, что это случайная выборка , полученная из непрерывного распределения с помощью cdf . Обозначив, мы получаем соответствующую случайную выборку из стандартного равномерного распределения . Обратите внимание, что статистика заказов также удовлетворяет требованиям . ${\displaystyle X_{1},X_{2},\ldots ,X_{n}}$ ${\displaystyle F_{X}}$ ${\displaystyle U_{i}=F_{X}(X_{i})}$ ${\displaystyle U_{1},\ldots ,U_{n}}$ ${\displaystyle U_{(i)}=F_{X}(X_{(i)})}$

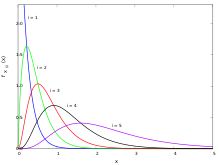
Функция плотности вероятности статистики порядка равна ^[3] ${\displaystyle U_{(k)}}$

${\displaystyle f_{U_{(k)}}(u)={n! \over (k-1)!(n-k)!}u^{k-1}(1-u)^{n-k}}$

то есть статистика k- го порядка равномерного распределения представляет собой случайную величину с бета-распределением . ^{[3] [4]}

${\displaystyle U_{(k)}\sim \operatorname {Beta} (k,n+1\mathbf {-} k).}$

Доказательство этих утверждений состоит в следующем. Чтобы находиться между u и u  +  du , необходимо, чтобы ровно k  − 1 элементов выборки были меньше u и чтобы хотя бы один находился между u и u  + d u . Вероятность того, что в этом последнем интервале окажется более одного, уже равна , поэтому нам нужно вычислить вероятность того, что ровно k  - 1, 1 и n  -  k наблюдений попадают в интервалы , и соответственно. Это равно ( подробнее см. Полиномиальное распределение ) ${\displaystyle U_{(k)}}$ ${\displaystyle O(du^{2})}$ ${\displaystyle (0,u)}$ ${\displaystyle (u,u+du)}$ ${\displaystyle (u+du,1)}$

${\displaystyle {n! \over (k-1)!(n-k)!}u^{k-1}\cdot du\cdot (1-u-du)^{n-k}}$

и результат следующий.

Среднее значение этого распределения равно k /( n + 1).

Совместное распределение статистики заказов равномерного распределения

Аналогично, для i  <  j можно показать, что совместная функция плотности вероятности статистики двух порядков U _{( i )}  <  U _{( j ) равна}

${\displaystyle f_{U_{(i)},U_{(j)}}(u,v)=n!{u^{i-1} \over (i-1)!}{(v-u)^{j-i-1} \over (j-i-1)!}{(1-v)^{n-j} \over (n-j)!}}$

что представляет собой (с точностью до членов более высокого порядка, чем ) вероятность того, что i  - 1, 1, j  - 1 -  i , 1 и n  -  j элементов выборки попадают в интервалы , , , соответственно . ${\displaystyle O(du\,dv)}$ ${\displaystyle (0,u)}$ ${\displaystyle (u,u+du)}$ ${\displaystyle (u+du,v)}$ ${\displaystyle (v,v+dv)}$ ${\displaystyle (v+dv,1)}$

Совершенно аналогичным образом можно рассуждать и о выводе совместных распределений более высокого порядка. Возможно, это удивительно, но совместная плотность статистики n- го порядка оказывается постоянной :

${\displaystyle f_{U_{(1)},U_{(2)},\ldots ,U_{(n)}}(u_{1},u_{2},\ldots ,u_{n})=n!.}$

Один из способов понять это состоит в том, что неупорядоченный образец действительно имеет постоянную плотность, равную 1, и что существует n ! разные перестановки выборки, соответствующие одной и той же последовательности статистики порядка. Это связано с тем, что 1/ n ! - объем региона . Это связано также с другой особенностью порядковой статистики однородных случайных величин: из BRS -неравенства следует , что максимальное ожидаемое число однородных U(0,1] случайных величин, которое можно выбрать из выборки размера n с суммой не превышающее ограничено сверху , что, таким образом, инвариантно на множестве всех с постоянным произведением . ${\displaystyle 0<u_{1}<\cdots <u_{n}<1}$ ${\displaystyle 0<s<n/2}$ ${\displaystyle {\sqrt {2sn}}}$ ${\displaystyle s,n}$ ${\displaystyle sn}$

Используя приведенные выше формулы, можно получить распределение диапазона статистики порядка, то есть распределение , то есть максимум минус минимум. В более общем смысле , для также имеет бета-распределение: ${\displaystyle U_{(n)}-U_{(1)}}$ ${\displaystyle n\geq k>j\geq 1}$ ${\displaystyle U_{(k)}-U_{(j)}}$

$${\displaystyle U_{(k)}-U_{(j)}\sim \operatorname {Beta} (k-j,n-(k-j)+1)}$$

$${\displaystyle \operatorname {Cov} (U_{(k)},U_{(j)})={\frac {j(n-k+1)}{(n+1)^{2}(n+2)}}}$$

$${\displaystyle \operatorname {Var} (U_{(k)}-U_{(j)})=\operatorname {Var} (U_{(k)})+\operatorname {Var} (U_{(j)})-2\cdot \operatorname {Cov} (U_{(k)},U_{(j)})={\frac {k(n-k+1)}{(n+1)^{2}(n+2)}}+{\frac {j(n-j+1)}{(n+1)^{2}(n+2)}}-2\cdot \operatorname {Cov} (U_{(k)},U_{(j)})}$$

$${\displaystyle \operatorname {Var} (U)={\frac {(k-j)(n-(k-j)+1)}{(n+1)^{2}(n+2)}}}$$

${\displaystyle U\sim \operatorname {Beta} (k-j,n-(k-j)+1)}$

Статистика заказов, полученная из экспоненциального распределения

Для случайной выборки размера n из экспоненциального распределения с параметром λ статистика порядка X _{( i )} для i = 1,2,3,..., n имеет распределение ${\displaystyle X_{1},X_{2},..,X_{n}}$

${\displaystyle X_{(i)}{\stackrel {d}{=}}{\frac {1}{\lambda }}\left(\sum _{j=1}^{i}{\frac {Z_{j}}{n-j+1}}\right)}$

где Z _j — стандартные экспоненциальные случайные величины iid (т.е. с параметром скорости 1). Этот результат был впервые опубликован Альфредом Реньи . ^{[5] [6]}

Статистика заказов, взятая из распределения Erlang

Преобразование Лапласа статистики порядка может быть выбрано из распределения Эрланга с помощью метода подсчета путей ^{[ необходимы пояснения ]} . ^[7]

Совместное распределение статистики заказов абсолютно непрерывного распределения

Если F _X абсолютно непрерывен , то он имеет такую ​​плотность , что и мы можем использовать замены ${\displaystyle dF_{X}(x)=f_{X}(x)\,dx}$

${\displaystyle u=F_{X}(x)}$

и

${\displaystyle du=f_{X}(x)\,dx}$

чтобы получить следующие функции плотности вероятности для статистики порядка выборки размера n , взятой из распределения X :

${\displaystyle f_{X_{(k)}}(x)={\frac {n!}{(k-1)!(n-k)!}}[F_{X}(x)]^{k-1}[1-F_{X}(x)]^{n-k}f_{X}(x)}$

${\displaystyle f_{X_{(j)},X_{(k)}}(x,y)={\frac {n!}{(j-1)!(k-j-1)!(n-k)!}}[F_{X}(x)]^{j-1}[F_{X}(y)-F_{X}(x)]^{k-1-j}[1-F_{X}(y)]^{n-k}f_{X}(x)f_{X}(y)}$где ${\displaystyle x\leq y}$

${\displaystyle f_{X_{(1)},\ldots ,X_{(n)}}(x_{1},\ldots ,x_{n})=n!f_{X}(x_{1})\cdots f_{X}(x_{n})}$где ${\displaystyle x_{1}\leq x_{2}\leq \dots \leq x_{n}.}$

Приложение: доверительные интервалы для квантилей.

Интересный вопрос заключается в том, насколько хорошо статистика порядка выполняет функцию оценки квантилей основного распределения.

Пример небольшого размера выборки

Самый простой случай, который следует рассмотреть, — насколько хорошо медиана выборки оценивает медиану совокупности.

В качестве примера рассмотрим случайную выборку размером 6. В этом случае медиана выборки обычно определяется как середина интервала, ограниченного статистикой 3-го и 4-го порядка. Однако из предыдущего обсуждения мы знаем, что вероятность того, что этот интервал действительно содержит медиану совокупности, равна ^{[ необходимы пояснения ]}

${\displaystyle {6 \choose 3}(1/2)^{6}={5 \over 16}\approx 31\%.}$

Хотя выборочная медиана, вероятно, является одной из лучших точечных оценок медианы совокупности, не зависящих от распределения, этот пример иллюстрирует то, что она не особенно хороша в абсолютном выражении. В этом конкретном случае лучшим доверительным интервалом для медианы является интервал, ограниченный статистикой 2-го и 5-го порядка, который содержит медиану совокупности с вероятностью

${\displaystyle \left[{6 \choose 2}+{6 \choose 3}+{6 \choose 4}\right](1/2)^{6}={25 \over 32}\approx 78\%.}$

При таком небольшом размере выборки, если кто-то хочет иметь уверенность не менее 95%, приходится говорить, что медиана находится между минимумом и максимумом из 6 наблюдений с вероятностью 31/32 или примерно 97%. Размер 6 фактически представляет собой наименьший размер выборки, при котором интервал, определяемый минимумом и максимумом, составляет как минимум 95% доверительный интервал для медианы генеральной совокупности.

Большие размеры выборки

Для равномерного распределения, когда n стремится к бесконечности, p- ^й квантиль выборки асимптотически нормально распределен , поскольку он аппроксимируется выражением

${\displaystyle U_{(\lceil np\rceil )}\sim AN\left(p,{\frac {p(1-p)}{n}}\right).}$

Для общего распределения F с непрерывной ненулевой плотностью в F  ⁻¹ ( p ) применяется аналогичная асимптотическая нормальность:

${\displaystyle X_{(\lceil np\rceil )}\sim AN\left(F^{-1}(p),{\frac {p(1-p)}{n[f(F^{-1}(p))]^{2}}}\right)}$

где f — функция плотности , а F  ⁻¹ — функция квантиля , связанная с F. Одним из первых, кто упомянул и доказал этот результат, был Фредерик Мостеллер в своей основополагающей статье в 1946 году. ^[8] Дальнейшие исследования привели в 1960-х годах к представлению Бахадура , которое предоставляет информацию о границах ошибок. Сходимость к нормальному распределению также имеет место в более сильном смысле, например, сходимость по относительной энтропии или КЛ-дивергенция . ^[9]

Интересное наблюдение можно сделать в случае, когда распределение симметрично, а медиана населения равна среднему значению населения. В этом случае выборочное среднее согласно центральной предельной теореме также асимптотически нормально распределено, но вместо этого с дисперсией σ ² /n . Этот асимптотический анализ предполагает, что среднее значение превосходит медиану в случаях низкого эксцесса , и наоборот. Например, медиана обеспечивает лучшие доверительные интервалы для распределения Лапласа , в то время как среднее работает лучше для X , которые имеют нормальное распределение.

Доказательство

Можно показать, что

${\displaystyle B(k,n+1-k)\ {\stackrel {\mathrm {d} }{=}}\ {\frac {X}{X+Y}},}$

где

${\displaystyle X=\sum _{i=1}^{k}Z_{i},\quad Y=\sum _{i=k+1}^{n+1}Z_{i},}$

где Z _i являются независимыми одинаково распределенными экспоненциальными случайными величинами с частотой 1. Поскольку X / n и Y / n асимптотически нормально распределяются с помощью CLT, наши результаты получены на основе применения дельта-метода .

Приложение: Непараметрическая оценка плотности.

Моменты распределения статистики первого порядка можно использовать для разработки непараметрической оценки плотности. ^[10] Предположим, мы хотим оценить плотность в точке . Рассмотрим случайные величины , которые имеют функцию распределения . В частности, . ${\displaystyle f_{X}}$ ${\displaystyle x^{*}}$ ${\displaystyle Y_{i}=|X_{i}-x^{*}|}$ ${\displaystyle g_{Y}(y)=f_{X}(y+x^{*})+f_{X}(x^{*}-y)}$ ${\displaystyle f_{X}(x^{*})={\frac {g_{Y}(0)}{2}}}$

Ожидаемое значение статистики первого порядка с учетом выборки общего количества наблюдений дает: ${\displaystyle Y_{(1)}}$ ${\displaystyle N}$

${\displaystyle E(Y_{(1)})={\frac {1}{(N+1)g(0)}}+{\frac {1}{(N+1)(N+2)}}\int _{0}^{1}Q''(z)\delta _{N+1}(z)\,dz}$

где – функция квантиля, связанная с распределением , и . Это уравнение в сочетании с методом складного ножа становится основой для следующего алгоритма оценки плотности: ${\displaystyle Q}$ ${\displaystyle g_{Y}}$ ${\displaystyle \delta _{N}(z)=(N+1)(1-z)^{N}}$

 Входные данные: выборка наблюдений. точки оценки плотности. Параметр настройки (обычно 1/3). ${\displaystyle N}$ ${\displaystyle \{x_{\ell }\}_{\ell =1}^{M}}$ ${\displaystyle a\in (0,1)}$ Выход: расчетная плотность в точках оценки. ${\displaystyle \{{\hat {f}}_{\ell }\}_{\ell =1}^{M}}$

 1: Набор 2: Набор 3: Создайте матрицу , содержащую подмножества с наблюдениями в каждом. ${\displaystyle m_{N}=\operatorname {round} (N^{1-a})}$ ${\displaystyle s_{N}={\frac {N}{m_{N}}}}$ ${\displaystyle s_{N}\times m_{N}}$ ${\displaystyle M_{ij}}$ ${\displaystyle m_{N}}$ ${\displaystyle s_{N}}$ 4: Создайте вектор для хранения оценок плотности. ${\displaystyle {\hat {f}}}$ 5: для  действия 6: для действия 7: Найти ближайшее расстояние до текущей точки в пределах th подмножества ${\displaystyle \ell =1\to M}$   ${\displaystyle k=1\to m_{N}}$  ${\displaystyle d_{\ell k}}$ ${\displaystyle x_{\ell }}$ ${\displaystyle k}$ 8: конец для 9: вычислить среднее подмножество расстояний до 10: вычислить оценку плотности в 11: конец для 12: возврат ${\displaystyle x_{\ell }:d_{\ell }=\sum _{k=1}^{m_{N}}{\frac {d_{\ell k}}{m_{N}}}}$ ${\displaystyle x_{\ell }:{\hat {f}}_{\ell }={\frac {1}{2(1+s_{N})d_{\ell }}}}$  ${\displaystyle {\hat {f}}}$

В отличие от параметров настройки на основе ширины полосы/длины для подходов на основе гистограммы и ядра , параметром настройки для оценки плотности на основе статистики порядка является размер подмножеств выборки. Такая оценка более надежна, чем подходы, основанные на гистограмме и ядре, например, такие плотности, как распределение Коши (в котором отсутствуют конечные моменты), можно вывести без необходимости специальных модификаций, таких как пропускная способность на основе IQR . Это связано с тем, что первый момент статистики порядка всегда существует, если существует ожидаемое значение основного распределения, но обратное не обязательно верно. ^[11]

Работа с дискретными переменными

Предположим , что это iid случайные величины из дискретного распределения с кумулятивной функцией распределения и функцией массы вероятности . Чтобы найти вероятности статистики заказов, сначала необходимы три значения, а именно: ${\displaystyle X_{1},X_{2},\ldots ,X_{n}}$ ${\displaystyle F(x)}$ ${\displaystyle f(x)}$ ${\displaystyle k^{\text{th}}}$

${\displaystyle p_{1}=P(X<x)=F(x)-f(x),\ p_{2}=P(X=x)=f(x),{\text{ and }}p_{3}=P(X>x)=1-F(x).}$

Кумулятивную функцию распределения статистики порядка можно вычислить, заметив, что ${\displaystyle k^{\text{th}}}$

${\displaystyle {\begin{aligned}P(X_{(k)}\leq x)&=P({\text{there are at least }}k{\text{ observations less than or equal to }}x),\\&=P({\text{there are at most }}n-k{\text{ observations greater than }}x),\\&=\sum _{j=0}^{n-k}{n \choose j}p_{3}^{j}(p_{1}+p_{2})^{n-j}.\end{aligned}}}$

Аналогично, дается ${\displaystyle P(X_{(k)}<x)}$

${\displaystyle {\begin{aligned}P(X_{(k)}<x)&=P({\text{there are at least }}k{\text{ observations less than }}x),\\&=P({\text{there are at most }}n-k{\text{ observations greater than or equal to }}x),\\&=\sum _{j=0}^{n-k}{n \choose j}(p_{2}+p_{3})^{j}(p_{1})^{n-j}.\end{aligned}}}$

Обратите внимание, что функция массы вероятности представляет собой просто разность этих значений, то есть ${\displaystyle X_{(k)}}$

${\displaystyle {\begin{aligned}P(X_{(k)}=x)&=P(X_{(k)}\leq x)-P(X_{(k)}<x),\\&=\sum _{j=0}^{n-k}{n \choose j}\left(p_{3}^{j}(p_{1}+p_{2})^{n-j}-(p_{2}+p_{3})^{j}(p_{1})^{n-j}\right),\\&=\sum _{j=0}^{n-k}{n \choose j}\left((1-F(x))^{j}(F(x))^{n-j}-(1-F(x)+f(x))^{j}(F(x)-f(x))^{n-j}\right).\end{aligned}}}$

Вычисление статистики заказов

Задача вычисления k- го наименьшего (или наибольшего) элемента списка называется проблемой выбора и решается с помощью алгоритма выбора. Хотя эта проблема сложна для очень больших списков, были созданы сложные алгоритмы выбора, которые могут решить эту проблему за время, пропорциональное количеству элементов в списке, даже если список совершенно неупорядочен. Если данные хранятся в определенных специализированных структурах данных, это время можно сократить до O(log n ). Во многих приложениях требуется вся статистика по порядку, и в этом случае можно использовать алгоритм сортировки , а затрачиваемое на это время составляет O( n log n ).

Смотрите также

• Ранкит
• Коробочный сюжет
• BRS-неравенство
• Сопутствующее (статистика)
• Распределение Фишера – Типпета
• Теорема Бапата–Бега о порядковой статистике независимых, но не обязательно одинаково распределенных случайных величин.
• Полином Бернштейна
• L-оценщик - линейные комбинации статистики заказов
• Распределение по рангам
• Алгоритм выбора

Примеры статистики заказов

• Примерный максимум и минимум
• Квантиль
• процентиль
• Дециль
• Квартиль
• медиана
• Иметь в виду
• Выборочное среднее и ковариация

Рекомендации

1. Дэвид, HA; Нагараджа, Х.Н. (2003). Статистика заказов . Ряд Уайли по вероятности и статистике. дои : 10.1002/0471722162. ISBN 9780471722168.
2. Казелла, Джордж; Бергер, Роджер (2002). Статистический вывод (2-е изд.). Cengage Обучение. п. 229. ИСБН 9788131503942.
3. Джентл, Джеймс Э. (2009), Вычислительная статистика, Springer, стр. 63, ISBN 9780387981444.
4. Джонс, MC (2009), «Распределение Кумарасвами: распределение бета-типа с некоторыми преимуществами управляемости», Статистическая методология , 6 (1): 70–81, doi : 10.1016/j.stamet.2008.04.001, Как и хорошо Как известно, бета-распределение — это распределение статистики m -го порядка из случайной выборки размера n из равномерного распределения (по (0,1)).
5. Дэвид, HA; Нагараджа, Х.Н. (2003), «Глава 2. Основная теория распределения», Статистика порядков , Ряды Вили по вероятности и статистике, стр. 9, дои : 10.1002/0471722162.ch2, ISBN 9780471722168
6. Реньи, Альфред (1953). «К теории порядковой статистики». Acta Mathematica Hungarica . 4 (3): 191–231. дои : 10.1007/BF02127580 .
7. Глинка, М.; Брилл, штат Пенсильвания; Хорн, В. (2010). «Метод получения преобразований Лапласа порядковой статистики случайных величин Эрланга». Статистика и вероятностные буквы . 80 : 9–18. дои : 10.1016/j.spl.2009.09.006.
8. Мостеллер, Фредерик (1946). «О некоторых полезных «неэффективных» статистических данных». Анналы математической статистики . 17 (4): 377–408. дои : 10.1214/aoms/1177730881 . Проверено 26 февраля 2015 г.
9. М. Кардоне, А. Дитсо и К. Раш, «Энтропийная центральная предельная теорема для статистики заказов», в IEEE Transactions on Information Theory, vol. 69, нет. 4, стр. 2193–2205, апрель 2023 г., doi: 10.1109/TIT.2022.3219344.
10. Гарг, Викрам В.; Тенорио, Луис; Уиллкокс, Карен (2017). «Оценка минимальной локальной плотности расстояний». Коммуникации в статистике - теория и методы . 46 (1): 148–164. arXiv : 1412.2851 . дои : 10.1080/03610926.2014.988260. S2CID  14334678.
11. Дэвид, HA; Нагараджа, Х.Н. (2003), «Глава 3. Ожидаемые значения и моменты», Статистика заказов , Ряды Вили в вероятности и статистике, стр. 34, дои : 10.1002/0471722162.ch3, ISBN 9780471722168

Внешние ссылки

• Заказать статистику на PlanetMath . Проверено 2 февраля 2005 г.
• Вайсштейн, Эрик В. «Статистика заказов». Математический мир .Проверено 2 февраля 2005 г.
• Статистика динамического порядка исходного кода C++