Статистика теста — это величина, полученная из выборки для статистической проверки гипотез . [1] Проверка гипотезы обычно определяется в терминах статистики теста, рассматриваемой как численное резюме набора данных, которое сводит данные к одному значению, которое может быть использовано для выполнения проверки гипотезы. В общем, статистика теста выбирается или определяется таким образом, чтобы количественно оценить в наблюдаемых данных поведение, которое отличало бы нулевую гипотезу от альтернативной , если такая альтернатива предписана, или которое характеризовало бы нулевую гипотезу, если нет явно заявленной альтернативной гипотезы.
Важным свойством тестовой статистики является то, что ее распределение выборки при нулевой гипотезе должно быть вычисляемым, либо точно, либо приблизительно, что позволяет вычислять p -значения . Тестовая статистика разделяет некоторые из тех же качеств описательной статистики , и многие статистики могут использоваться как в качестве тестовой статистики, так и в качестве описательной статистики. Однако тестовая статистика специально предназначена для использования в статистическом тестировании, тогда как основным качеством описательной статистики является то, что ее легко интерпретировать. Некоторые информативные описательные статистики, такие как выборочный диапазон , не являются хорошей тестовой статистикой, поскольку трудно определить их выборочное распределение.
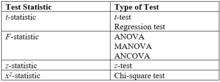
Двумя широко используемыми тестовыми статистиками являются t-статистика и F-статистика .
Предположим, что задача состоит в том, чтобы проверить, является ли монета честной (т. е. имеет ли она равные вероятности выпадения орла или решки). Если монета подбрасывается 100 раз и результаты записываются, то необработанные данные можно представить в виде последовательности из 100 орлов и решек. Если интерес представляет предельная вероятность выпадения решки, необходимо записать только число T из 100 подбрасываний, в результате которых выпала решка. Но T также можно использовать в качестве тестовой статистики одним из двух способов:
Используя одно из этих распределений выборки, можно вычислить одностороннее или двустороннее p-значение для нулевой гипотезы о том, что монета является честной. Тестовая статистика в этом случае сокращает набор из 100 чисел до одной числовой сводки, которую можно использовать для проверки.
Одновыборочные тесты подходят, когда выборка сравнивается с популяцией из гипотезы. Характеристики популяции известны из теории или рассчитываются на основе популяции.
Двухвыборочные тесты подходят для сравнения двух образцов, как правило, экспериментальных и контрольных образцов из научно контролируемого эксперимента.
Парные тесты подходят для сравнения двух выборок, когда невозможно контролировать важные переменные. Вместо того, чтобы сравнивать два набора, члены парируются между выборками, так что разница между членами становится выборкой. Обычно среднее значение разностей затем сравнивается с нулем. Обычный пример сценария, когда парный тест разностей подходит, — это когда к одному набору испытуемых что-то применяется, и тест предназначен для проверки эффекта.
Z-тесты подходят для сравнения средних значений в строгих условиях относительно нормальности и известного стандартного отклонения.
Для сравнения средних значений в смягченных условиях (предполагается меньшее) подходит t - тест .
Тесты пропорций аналогичны тестам средних значений (50%-ная пропорция).
Тесты хи-квадрат используют одни и те же вычисления и одно и то же распределение вероятностей для разных приложений:
F-тесты (дисперсионный анализ, ANOVA) обычно используются при принятии решения о том, имеет ли смысл группировка данных по категориям. Если дисперсия результатов тестов левшей в классе намного меньше дисперсии всего класса, то может быть полезно изучать левшей как группу. Нулевая гипотеза заключается в том, что две дисперсии одинаковы, поэтому предлагаемая группировка не имеет смысла.
В таблице ниже используемые символы определены в нижней части таблицы. Многие другие тесты можно найти в других статьях . Существуют доказательства того, что статистика теста является подходящей. [2]