Статическое рассеяние света

Статическое рассеяние света — это метод в физической химии , который измеряет интенсивность рассеянного света для получения средней молекулярной массы M _w макромолекулы, такой как полимер или белок в растворе. Измерение интенсивности рассеяния под многими углами позволяет вычислить среднеквадратичный радиус, также называемый радиусом инерции R _g . Измеряя интенсивность рассеяния для многих образцов различных концентраций, можно вычислить второй вириальный коэффициент, A ₂ ^{. [1] [2] [3] [4] [5]}

Статическое рассеяние света также широко используется для определения размера суспензий частиц в субмкм и супра-мкм диапазонах с помощью формализмов Лоренца-Ми (см. Рассеяние Ми ) и дифракции Фраунгофера соответственно.

Для экспериментов по статическому рассеянию света высокоинтенсивный монохроматический свет, обычно лазер, запускается в раствор, содержащий макромолекулы. Один или несколько детекторов используются для измерения интенсивности рассеяния под одним или несколькими углами. Угловая зависимость необходима для получения точных измерений как молярной массы, так и размера для всех макромолекул с радиусом более 1–2% от длины волны падающего света. Поэтому одновременные измерения под несколькими углами относительно направления падающего света, известные как многоугловое рассеяние света (MALS) или многоугловое рассеяние лазерного света (MALLS), обычно считаются стандартной реализацией статического рассеяния света. Дополнительные сведения об истории и теории MALS можно найти в многоугловом рассеянии света .

Для измерения средней молекулярной массы напрямую без калибровки по интенсивности рассеяния света необходимо знать интенсивность лазера, квантовую эффективность детектора, а также полный объем рассеяния и телесный угол детектора. Поскольку это непрактично, все коммерческие приборы калибруются с использованием сильного известного рассеивателя, например толуола , поскольку отношение Рэлея толуола и нескольких других растворителей измерялось с использованием прибора абсолютного рассеяния света.

Теория

Для прибора рассеяния света, состоящего из множества детекторов, расположенных под разными углами, все детекторы должны реагировать одинаково. Обычно детекторы будут иметь немного различную квантовую эффективность , разный коэффициент усиления и смотреть на разные геометрические объемы рассеяния. В этом случае нормализация детекторов абсолютно необходима. Чтобы нормализовать детекторы, сначала выполняется измерение чистого растворителя. Затем к растворителю добавляется изотропный рассеиватель. Поскольку изотропные рассеиватели рассеивают одинаковую интенсивность под любым углом, эффективность и коэффициент усиления детектора можно нормализовать с помощью этой процедуры. Удобно нормализовать все детекторы к детектору под углом 90°.

${\displaystyle \ N(\theta )={\frac {I_{R}(\theta )-I_{S}(\theta )}{I_{R}(90)-I_{S}(90)}}}$

где I _R (90) — интенсивность рассеяния, измеренная для рассеивателя Рэлея с помощью детектора под углом 90°.

Наиболее распространенным уравнением для измерения средневзвешенной молекулярной массы, M _w , является уравнение Зимма ^[5] (правая часть уравнения Зимма в некоторых текстах указана неверно, как отмечают Хименц и Лодж): ^[6]

${\displaystyle {\frac {Kc}{\Delta R(\theta ,c)}}={\frac {1}{M_{w}}}\left(1+{\frac {q^{2}R_{g}^{2}}{3}}+O(q^{4})\right)+2A_{2}c+O(c^{2})}$

где

${\displaystyle \ K=4\pi ^{2}n_{0}^{2}(dn/dc)^{2}/N_{\text{A}}\lambda ^{4}}$

и

${\displaystyle \ \Delta R(\theta ,c)=R_{A}(\theta )-R_{0}(\theta )}$

с

${\displaystyle \ R(\theta )={\frac {I_{A}(\theta )n_{0}^{2}}{I_{T}(\theta )n_{T}^{2}}}{\frac {R_{T}}{N(\theta )}}}$

а вектор рассеяния для вертикально поляризованного света равен

${\displaystyle \ q=4\pi n_{0}\sin(\theta /2)/\lambda }$

где n _{0 —} показатель преломления растворителя, λ — длина волны источника света, N _A — постоянная Авогадро , c — концентрация раствора, а d n /d c — изменение показателя преломления раствора при изменении концентрации. Интенсивность аналита, измеренная под углом, равна I _A (θ) . В этих уравнениях нижний индекс A относится к аналиту (раствору), а T — к толуолу с отношением Рэлея толуола, R _T составляет 1,35×10−5 ^см  − ¹ для HeNe-лазера . Как описано выше, радиус инерции, R _g , и второй вириальный коэффициент, A ₂ , также рассчитываются из этого уравнения. Приращение показателя преломления dn/dc характеризует изменение показателя преломления n с концентрацией c и может быть измерено с помощью дифференциального рефрактометра.

График Зимма строится из двойной экстраполяции к нулевому углу и нулевой концентрации из многих углов и многих измерений концентрации. В своей простейшей форме уравнение Зимма сводится к:

${\displaystyle \ Kc/\Delta R(\theta \rightarrow 0,c\rightarrow 0)=1/M_{w}}$

для измерений, выполненных под малым углом и при бесконечном разбавлении, поскольку P (0) = 1.

Обычно существует несколько анализов, разработанных для анализа рассеяния частиц в растворе, чтобы получить вышеназванные физические характеристики частиц. Простой статический эксперимент по рассеянию света подразумевает, что средняя интенсивность образца, скорректированная с учетом рассеяния растворителя, даст отношение Рэлея, R, как функцию угла или волнового вектора q следующим образом:

Анализ данных

участок Гинье

Интенсивность рассеяния можно изобразить в виде функции угла, чтобы получить информацию о R _{g ,} которую можно просто рассчитать с помощью приближения Гинье следующим образом:

${\displaystyle \ln(\Delta R(\theta ))=1-(R_{g}^{2}/3)q^{2}}$

где ln(ΔR(θ)) = lnP(θ), также известный как форм-фактор с q = 4πn ₀ sin(θ/2)/λ . Следовательно, график скорректированного отношения Рэлея, ΔR(θ) против sin ² (θ/2) или q ² даст наклон R _g ² /3 . Однако это приближение верно только для qR _g < 1 . Обратите внимание, что для графика Гинье значение dn/dc и концентрация не нужны.

Краткий участок

График Кратки обычно используется для анализа конформации белков , но может быть использован для анализа модели случайного блуждания полимеров . График Кратки может быть построен путем построения графика sin ² (θ/2)ΔR(θ) против sin(θ/2) или q ² ΔR(θ) против q .

Оценка статического измерения рассеяния света с использованием графика Зимма

участок Зимма

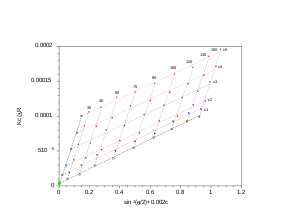
Для полимеров и полимерных комплексов, которые являются монодисперсными ( ), как это определено с помощью статического рассеяния света, график Зимма является обычным средством вывода таких параметров, как R _g , молекулярная масса M _w и второй вириальный коэффициент A ₂ . ${\displaystyle \scriptstyle \mu _{2}/{\bar {\Gamma }}^{2}<0.3}$

Следует отметить, что если константа материала K не реализована, график Зимма даст только R _g . Следовательно, реализация K даст следующее уравнение:

${\displaystyle {\frac {Kc}{\Delta R(\theta ,c)}}={\frac {1}{M_{w}}}\left(1+{\frac {q^{2}R_{g}^{2}}{3}}+O(q^{4})\right)+2A_{2}c+O(c^{2})}$

Анализ, выполненный с помощью графика Зимма, использует двойную экстраполяцию к нулевой концентрации и нулевому углу рассеяния, что приводит к характерному ромбовидному графику. Поскольку угловая информация доступна, также можно получить радиус инерции ( R _g ). Эксперименты проводятся под несколькими углами, которые удовлетворяют условию и по крайней мере 4 концентрациям. Выполнение анализа Зимма на одной концентрации известно как частичный анализ Зимма и действительно только для разбавленных растворов сильных точечных рассеивателей. Однако частичный анализ Зимма не дает второго вириального коэффициента из-за отсутствия переменной концентрации образца. Более конкретно, значение второго вириального коэффициента либо предполагается равным нулю, либо вводится как известное значение для выполнения частичного анализа Зимма. ${\displaystyle qR_{g}<1}$

Дебаевский график

Расчет молекулярной массы методом статического измерения рассеяния света с использованием графика Дебая ^[7]

Если измеренные частицы меньше λ/20, то форм-фактором P(θ) можно пренебречь ( P(θ) →1). Поэтому уравнение Зимма упрощается до уравнения Дебая следующим образом:

${\displaystyle {\frac {Kc}{\Delta R(\theta ,c)}}={\frac {1}{M_{w}}}+2A_{2}c}$

Обратите внимание, что это также результат экстраполяции к нулевому углу рассеяния. Получая данные о концентрации и интенсивности рассеяния, строится график Дебая путем построения графика Kc / ΔR(θ) против концентрации. Пересечение подобранной линии дает молекулярную массу, а наклон соответствует 2-му вириальному коэффициенту.

Поскольку график Дебая является упрощением уравнения Зимма, применяются те же ограничения последнего, то есть образцы должны иметь монодисперсную природу. Для полидисперсных образцов результирующая молекулярная масса из статического измерения рассеяния света будет представлять собой среднее значение. Преимуществом графика Дебая является возможность определения второго вириального коэффициента. Этот параметр описывает взаимодействие между частицами и растворителем. Например, в растворах макромолекул он может принимать отрицательные (взаимодействия частица-частица предпочтительны), нулевые или положительные значения (взаимодействия частица-растворитель предпочтительны). ^[8]

Многократное рассеяние

Статическое рассеяние света предполагает, что каждый обнаруженный фотон был рассеян только один раз. Поэтому анализ в соответствии с приведенными выше расчетами будет правильным только в том случае, если образец был достаточно разбавлен, чтобы гарантировать, что фотоны не будут рассеиваться образцом несколько раз до того, как будут обнаружены. Точная интерпретация становится чрезвычайно сложной для систем с существенным вкладом многократного рассеяния. Во многих коммерческих приборах, где анализ сигнала рассеяния выполняется автоматически, ошибка может никогда не быть замечена пользователем. В частности, для более крупных частиц и частиц с высоким контрастом показателя преломления, это ограничивает применение стандартного статического рассеяния света очень низкими концентрациями частиц. С другой стороны, для растворимых макромолекул, которые демонстрируют относительно низкий контраст показателя преломления по сравнению с растворителем, включая большинство полимеров и биомолекул в их соответствующих растворителях, многократное рассеяние редко является ограничивающим фактором даже при концентрациях, приближающихся к пределам растворимости.

Однако, как показал Шетцель ^[9], можно подавить многократное рассеяние в экспериментах по статическому рассеянию света с помощью подхода кросс-корреляции. Общая идея заключается в том, чтобы изолировать однократно рассеянный свет и подавить нежелательные вклады многократного рассеяния в эксперименте по статическому рассеянию света. Были разработаны и применены различные реализации кросс-корреляционного рассеяния света. В настоящее время наиболее широко используемой схемой является так называемый метод 3D-динамического рассеяния света. ^{[10] [11]} Этот же метод можно использовать для коррекции данных динамического рассеяния света для вкладов многократного рассеяния. ^[12]

Статическое рассеяние света с градиентом состава

Образцы, которые меняют свои свойства после разбавления, не могут быть проанализированы с помощью статического рассеяния света в терминах простой модели, представленной здесь как уравнение Зимма. Более сложный анализ, известный как «статическое (или многоугловое) рассеяние света с градиентом состава» (CG-SLS или CG-MALS), является важным классом методов для исследования белок-белковых взаимодействий , коллигативных свойств и других макромолекулярных взаимодействий, поскольку он дает, в дополнение к размеру и молекулярной массе, информацию о сродстве и стехиометрии молекулярных комплексов, образованных одним или несколькими ассоциированными макромолекулярными/биомолекулярными видами. В частности, статическое рассеяние света из серии разбавлений может быть проанализировано для количественной оценки самоассоциации, обратимой олигомеризации и неспецифического притяжения или отталкивания, в то время как статическое рассеяние света из смесей видов может быть проанализировано для количественной оценки гетероассоциации. ^[13]

Приложения

Одно из основных применений статического рассеяния света для определения молекулярной массы — это область макромолекул, таких как белки и полимеры, ^{[14] [15] [16],} поскольку можно измерить молекулярную массу белков без каких-либо предположений об их форме. Статическое рассеяние света обычно сочетается с другими методами характеризации частиц, такими как гель-хроматография (SEC), динамическое рассеяние света (DLS) и электрофоретическое рассеяние света (ELS).

Смотрите также

• Дифференциальное статическое рассеяние света (DSLS)
• Динамическое рассеяние света
• Рассеивание света
• Белково-белковые взаимодействия

Ссылки

1. А. Эйнштейн (1910). «Теория опалесценции von homogenen Flüssigkeiten und Flüssigkeitsgemischen in der Nähe des kritischen Zustandes». Анналы физики . 33 (16): 1275. Бибкод : 1910АнП...338.1275Е. дои : 10.1002/andp.19103381612.
2. CV Raman (1927). «Связь эффекта Тиндаля с осмотическим давлением в коллоидных растворах». Indian J. Phys . 2 : 1.
3. P.Debye (1944). "Рассеяние света в растворах". J. Appl. Phys . 15 (4): 338. Bibcode :1944JAP....15..338D. doi :10.1063/1.1707436.
4. BH Zimm (1945). "Молекулярная теория рассеяния света в жидкостях". J. Chem. Phys . 13 (4): 141. Bibcode :1945JChPh..13..141Z. doi :10.1063/1.1724013.
5. BH Zimm (1948). "Рассеяние света и радиальная функция распределения растворов высокополимеров". J. Chem. Phys . 16 (12): 1093. Bibcode :1948JChPh..16.1093Z. doi :10.1063/1.1746738.
6. Хименц, Пол С.; Лодж, Тимоти П. (2007). Химия полимеров (2-е изд.). Бока-Ратон, Флорида [ua]: CRC Press. стр. 307–308. ISBN 978-1-57444-779-8.
7. "Измерение молекулярной массы с использованием статического рассеяния света :: Anton Paar Wiki". Anton Paar . Получено 23 сентября 2022 г. .
8. Чанг, Цин (2016), «Осмотическое давление», Коллоидная и интерфейсная химия для контроля качества воды , Elsevier, стр. 37–47, doi :10.1016/b978-0-12-809315-3.00004-9, ISBN 978-0-12-809315-3, получено 14 июня 2022 г.
9. Schaetzel, K. (1991). «Подавление многократного рассеяния методами кросс-корреляции фотонов». J. Mod. Opt . 38 : SA393–SA398. Bibcode :1990JPCM....2..393S. doi :10.1088/0953-8984/2/S/062. S2CID  250745836.
10. Urban, C.; Schurtenberger, P. (1998). «Характеристика мутных коллоидных суспензий с использованием методов рассеяния света в сочетании с методами кросс-корреляции». J. Colloid Interface Sci . 207 (1): 150–158. Bibcode :1998JCIS..207..150U. doi :10.1006/jcis.1998.5769. PMID  9778402.
11. Блок, И.; Шеффолд, Ф. (2010). «Модулированное 3D кросс-корреляционное рассеяние света: улучшение характеристики мутных образцов». Обзор научных инструментов . 81 (12): 123107–123107–7. arXiv : 1008.0615 . Bibcode :2010RScI...81l3107B. doi :10.1063/1.3518961. PMID  21198014. S2CID  9240166.
12. Pusey, PN (1999). «Подавление многократного рассеяния методами кросс-корреляции фотонов». Current Opinion in Colloid & Interface Science . 4 (3): 177–185. doi :10.1016/S1359-0294(99)00036-9.
13. Some, D. (2013). «Анализ биомолекулярных взаимодействий на основе рассеяния света». Biophys. Rev. 5 ( 2): 147–158. doi :10.1007/s12551-013-0107-1. PMC 3641300. PMID  23646069 . 
14. Sedlák, Marián (1 марта 2006 г.). «Крупномасштабная супрамолекулярная структура в растворах соединений с низкой молярной массой и смесях жидкостей: I. Характеристика рассеяния света». The Journal of Physical Chemistry B . 110 (9): 4329–4338. doi :10.1021/jp0569335. ISSN  1520-6106. PMID  16509731.
15. Диас-Ласприлла, Ана М.; Меркадо, Рональд А.; Рамирес-Кабальеро, Густаво Э. (20 июня 2021 г.). «Влияние степени полимеризации глицерина на эмульгирующие свойства полиглицериновых эфиров». Журнал прикладной полимерной науки . 138 (24): 50566. doi :10.1002/app.50566. ISSN  0021-8995. S2CID  233888953.
16. "Димеризация бычьего сывороточного альбумина, подтвержденная измерением размера частиц и молекулярной массы :: Anton-Paar.com". Anton Paar . Получено 14 июня 2022 г. .

Внешние ссылки

• Применение статического рассеяния света
• Litesizer