
В теории графов стягивание ребер — это операция , которая удаляет ребро из графа , одновременно объединяя две вершины , которые оно ранее соединило. Стягивание ребер — это фундаментальная операция в теории миноров графа . Идентификация вершин — менее ограничительная форма этой операции.
Операция сжатия ребра выполняется относительно конкретного ребра, . Ребро удаляется, а две его инцидентные вершины, и , объединяются в новую вершину , где ребра, инцидентные каждому, соответствуют ребру, инцидентному либо , либо . В более общем смысле, операция может быть выполнена над набором ребер путем сжатия каждого ребра (в любом порядке). [1]
Полученный граф иногда записывается как . (Сравните это с , что означает простое удаление ребра без объединения его инцидентных вершин.)
Как определено ниже, операция сокращения ребер может привести к графу с несколькими ребрами , даже если исходный граф был простым графом . [2] Однако некоторые авторы [3] запрещают создание нескольких ребер, поэтому сокращения ребер, выполняемые на простых графах, всегда приводят к простым графам.
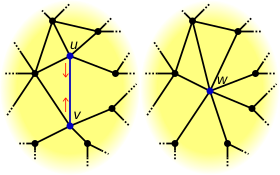
Пусть будет графом ( или ориентированным графом ), содержащим ребро с . Пусть будет функцией, которая отображает каждую вершину в себе, а в противном случае отображает ее в новую вершину . Сжатие приводит к новому графу , где , , и для каждого , инцидентно ребру тогда и только тогда, когда соответствующее ребро инцидентно в .
Идентификация вершин (иногда называемая стягиванием вершин ) снимает ограничение, что стягивание должно происходить над вершинами, разделяющими инцидентное ребро. (Таким образом, стягивание ребер является особым случаем идентификации вершин.) Операция может выполняться над любой парой (или подмножеством) вершин в графе. Ребра между двумя стягивающимися вершинами иногда удаляются. Если и являются вершинами различных компонентов , то мы можем создать новый граф , идентифицируя и в как новую вершину в . [4] В более общем смысле, если задано разбиение множества вершин, можно идентифицировать вершины в разбиении; полученный граф известен как фактор-граф .
Расщепление вершин , что то же самое, что и расщепление вершин, означает, что одна вершина разделяется на две, где эти две новые вершины являются смежными с вершинами, с которыми была смежной исходная вершина. Это обратная операция идентификации вершин, хотя в общем случае для идентификации вершин смежные вершины двух идентифицированных вершин не являются одним и тем же набором.
Сокращение пути происходит на множестве ребер в пути , которые сжимаются , чтобы сформировать одно ребро между конечными точками пути. Ребра, инцидентные вершинам вдоль пути, либо устраняются, либо произвольно (или систематически) соединяются с одной из конечных точек.
Рассмотрим два непересекающихся графа и , где содержит вершины и и содержит вершины и . Предположим, что мы можем получить граф , отождествляя вершины и как вершину и отождествляя вершины и как вершину . При скручивании относительно множества вершин мы отождествляем , вместо этого, с и с . [ 5]
Методы сокращения как ребер, так и вершин полезны при доказательстве методом индукции по числу вершин или ребер в графе, когда можно предположить, что свойство выполняется для всех меньших графов, и это можно использовать для доказательства свойства для большего графа.
Сокращение ребер используется в рекурсивной формуле для числа остовных деревьев произвольного связного графа [ 6] и в рекуррентной формуле для хроматического многочлена простого графа [7] .
Сокращения также полезны в структурах, где мы хотим упростить граф, определив вершины, которые представляют по существу эквивалентные сущности. Одним из наиболее распространенных примеров является сведение общего направленного графа к ациклическому направленному графу путем сокращения всех вершин в каждом сильно связанном компоненте . Если отношение, описываемое графом, является транзитивным , никакая информация не теряется, пока мы помечаем каждую вершину набором меток вершин, которые были сокращены для ее формирования.
Другим примером является объединение, выполняемое при распределении регистров глобальной раскраски графа , где вершины стягиваются (там, где это безопасно) для устранения операций перемещения между отдельными переменными.
Сокращение ребер используется в пакетах 3D-моделирования (либо вручную, либо с помощью какой-либо функции программного обеспечения для моделирования) для последовательного уменьшения количества вершин, что способствует созданию низкополигональных моделей.