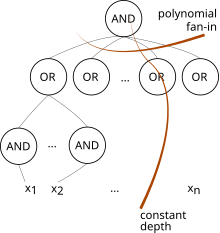
AC 0 — это класс сложности , используемый в сложности схемы . Это наименьший класс в иерархии AC , состоящий из всех семейств схем глубины O(1) и полиномиального размера с неограниченным числом вентилей И и ИЛИ (мы допускаем вентили НЕ только на входах). [1] Таким образом, он содержит NC 0 , который имеет только ограниченные числа вентилей И и ИЛИ. [1]
Сложение и вычитание целых чисел вычислимы в AC 0 [2], но умножение — нет (в частности, когда входными данными являются два целых числа в обычном двоичном [3] или десятичном представлении целых чисел).
Поскольку это класс схем, как и P/poly , AC 0 также содержит все унарные языки .
С точки зрения дескриптивной сложности DLOGTIME - uniform AC 0 равен дескриптивному классу FO +BIT всех языков, описываемых в логике первого порядка с добавлением предиката BIT , или альтернативно с помощью FO(+, ×), или с помощью машины Тьюринга в логарифмической иерархии . [4]
В 1984 году Фурст, Сакс и Сипсер показали, что вычисление четности входных битов (в отличие от вышеупомянутых задач сложения/вычитания, которые имели два входа) не может быть решено никакими схемами AC 0 , даже с неоднородностью. [5] [1] Из этого следует, что AC 0 не равно NC 1 , поскольку семейство схем в последнем классе может вычислять четность. [1] Более точные границы следуют из леммы о переключении . Используя их, было показано, что существует разделение оракулов между иерархией полиномов и PSPACE .