Тест на перестановку

Точная статистическая проверка гипотезы

Тест на перестановку (также называемый тестом повторной рандомизации или тестом перестановки) — это точный статистический тест гипотез , в котором используется доказательство от противного . Тест на перестановку включает в себя две или более выборки. Нулевая гипотеза состоит в том, что все выборки происходят из одного и того же распределения . В соответствии с нулевой гипотезой распределение тестовой статистики получается путем расчета всех возможных значений тестовой статистики при возможных перестановках наблюдаемых данных. Таким образом, тесты на перестановку являются формой повторной выборки . ${\displaystyle H_{0}:F=G}$

Тесты на перестановки можно понимать как тестирование суррогатных данных , при котором суррогатные данные в соответствии с нулевой гипотезой получаются путем перестановок исходных данных. ^[1]

Другими словами, метод, с помощью которого лечение распределяется между субъектами в экспериментальном плане, отражается в анализе этого плана. Если метки взаимозаменяемы при нулевой гипотезе, то полученные тесты дают точные уровни значимости; см. также возможность замены . Затем на основе тестов можно получить доверительные интервалы. Эта теория возникла на основе работ Рональда Фишера и Э. Дж. Питмана 1930-х годов.

Перестановочные тесты не следует путать со рандомизированными тестами . ^[2]

Метод

Анимация теста перестановки, вычисляемого на наборах из 4 и 5 случайных значений. 4 значения красного цвета взяты из одного распределения, а 5 значений синего цвета — из другого; мы хотели бы проверить, различны ли средние значения двух распределений. Гипотеза состоит в том, что среднее значение первого распределения выше среднего значения второго; нулевая гипотеза состоит в том, что обе группы выборок взяты из одного и того же распределения. Существует 126 различных способов поместить 4 значения в одну группу и 5 в другую (9-выберите-4 или 9-выберите-5). Из них один соответствует исходной маркировке, а остальные 125 представляют собой «перестановки», которые генерируют показанную гистограмму средних различий . Значение p гипотезы оценивается как доля перестановок, которые дают разницу, большую или большую, чем разница средних исходных выборок. В этом примере нулевую гипотезу нельзя отвергнуть на уровне p = 5% . ${\displaystyle {\hat {\mu }}_{1}-{\hat {\mu }}_{2}}$

Чтобы проиллюстрировать основную идею теста перестановки, предположим, что мы собираем случайные переменные и для каждого человека из двух групп , чьи выборочные средние равны и , и что мы хотим знать, происходят ли и из одного и того же распределения. Пусть и — размер выборки, собранной из каждой группы. Тест на перестановку предназначен для определения того, достаточно ли велика наблюдаемая разница между выборочными средними, чтобы отвергнуть на некотором уровне значимости нулевую гипотезу H о том, что данные, полученные из, относятся к тому же распределению, что и данные, полученные из . ${\displaystyle X_{A}}$ ${\displaystyle X_{B}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle {\bar {x}}_{A}}$ ${\displaystyle {\bar {x}}_{B}}$ ${\displaystyle X_{A}}$ ${\displaystyle X_{B}}$ ${\displaystyle n_{A}}$ ${\displaystyle n_{B}}$ ${\displaystyle _{0}}$ ${\displaystyle A}$ ${\displaystyle B}$

Тест проходит следующим образом. Сначала рассчитывается разница средних значений между двумя выборками: это наблюдаемое значение тестовой статистики . ${\displaystyle T_{\text{obs}}}$

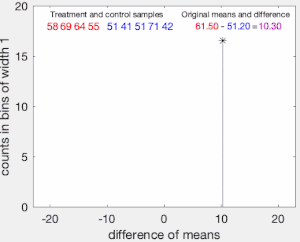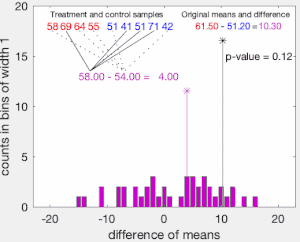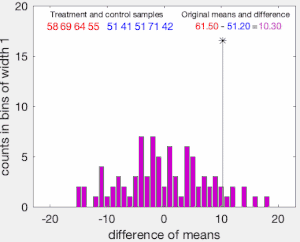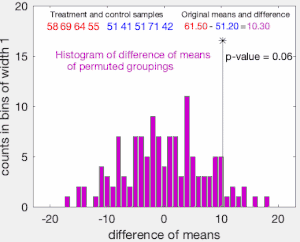
Затем наблюдения групп и объединяются, а разница в выборочных средних рассчитывается и записывается для каждого возможного способа разделения объединенных значений на две группы по размеру и (т. е. для каждой перестановки групповых меток A и B). Набор этих рассчитанных различий представляет собой точное распределение возможных различий (для этой выборки) при нулевой гипотезе о том, что групповые метки взаимозаменяемы (т. е. назначаются случайным образом). ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle n_{A}}$ ${\displaystyle n_{B}}$

Одностороннее значение p теста рассчитывается как доля выбранных перестановок, в которых разница в средних значениях превышала . Двустороннее значение p теста рассчитывается как доля выборочных перестановок, в которых абсолютная разница была больше . Многие реализации тестов перестановок требуют, чтобы сами наблюдаемые данные учитывались как одна из перестановок, чтобы p-значение перестановки никогда не было равно нулю. ^[3] ${\displaystyle T_{\text{obs}}}$ ${\displaystyle |T_{\text{obs}}|}$

В качестве альтернативы, если единственная цель теста — отвергнуть или не отвергнуть нулевую гипотезу, можно отсортировать записанные различия, а затем проверить, содержатся ли они в среднем % из них для некоторого уровня значимости . Если это не так, мы отвергаем гипотезу об идентичности кривых вероятности на уровне значимости. ${\displaystyle T_{\text{obs}}}$ ${\displaystyle (1-\alpha )\times 100}$ ${\displaystyle \alpha }$ ${\displaystyle \alpha \times 100\%}$

Для парных выборок необходимо применить тест парной перестановки.

Связь с параметрическими тестами

Тесты на перестановку — это подмножество непараметрической статистики . Предполагая, что наши экспериментальные данные получены на основе данных, измеренных в двух группах лечения, метод просто генерирует распределение средних различий в предположении, что две группы не различаются с точки зрения измеряемой переменной. Исходя из этого, затем можно использовать наблюдаемую статистику ( выше), чтобы увидеть, в какой степени эта статистика является особенной, т. е. вероятность наблюдения величины такого значения (или большего), если метки лечения были просто рандомизированы после лечения. ${\displaystyle T_{\text{obs}}}$

В отличие от тестов перестановки, распределения, лежащие в основе многих популярных «классических» статистических тестов, таких как t -test , F -test , z -test и χ ² test , получены из теоретических распределений вероятностей . Точный тест Фишера является примером часто используемого теста перестановки для оценки связи между двумя дихотомическими переменными. Когда размеры выборки очень велики, критерий хи-квадрат Пирсона даст точные результаты. Для небольших выборок нельзя предположить, что эталонное распределение хи-квадрат дает правильное описание распределения вероятностей тестовой статистики, и в этой ситуации использование точного критерия Фишера становится более подходящим.

Тесты на перестановку существуют во многих ситуациях, когда параметрические тесты отсутствуют (например, при построении оптимального теста, когда потери пропорциональны размеру ошибки, а не ее квадрату). Все простые и многие относительно сложные параметрические тесты имеют соответствующую версию теста перестановок, которая определяется с использованием той же статистики теста, что и параметрический тест, но получает значение p из распределения перестановок этой статистики для конкретной выборки, а не из теоретического распределение, полученное на основе параметрического предположения. Например, таким образом можно построить перестановочный t -тест , перестановочный тест ассоциации, перестановочную версию теста Али для сравнения дисперсий и так далее. ${\textstyle \chi ^{2}}$

Основным недостатком перестановочных тестов является то, что они

• Может требовать больших вычислительных ресурсов и может потребовать «собственного» кода для трудновычислимой статистики. Это необходимо переписывать для каждого случая.
• В основном используются для определения значения p. Инверсия теста для получения доверительных областей/интервалов требует еще большего объема вычислений.

Преимущества

Критерии перестановки существуют для любой тестовой статистики, независимо от того, известно ли ее распределение. Таким образом, каждый всегда свободен в выборе статистики, которая лучше всего различает гипотезу и альтернативу и которая минимизирует потери.

Тесты на перестановку можно использовать для анализа несбалансированных планов ^[4] и для объединения зависимых тестов на смеси категориальных, порядковых и метрических данных (Pesarin, 2001) ^{[ нужна ссылка ]} . Их также можно использовать для анализа качественных данных, которые были обработаны количественно (т. е. преобразованы в числа). Тесты перестановок могут быть идеальными для анализа квантованных данных, которые не удовлетворяют статистическим предположениям, лежащим в основе традиционных параметрических тестов (например, t-тесты, ANOVA), ^[5] см. PERMANOVA .

До 1980-х годов бремя создания эталонного распределения было непосильным, за исключением наборов данных с небольшим размером выборки.

С 1980-х годов появление относительно недорогих быстрых компьютеров и разработка новых сложных алгоритмов путей, применимых в особых ситуациях, сделали применение методов перестановочного тестирования практичным для решения широкого круга задач. Он также инициировал добавление опций точного теста в основные пакеты статистического программного обеспечения и появление специализированного программного обеспечения для выполнения широкого спектра точных тестов с одной и несколькими переменными и расчета «точных» доверительных интервалов на основе тестов.

Ограничения

Важным предположением, лежащим в основе теста перестановки, является то, что наблюдения можно обменивать при нулевой гипотезе. Важным следствием этого предположения является то, что тесты на различие в местоположении (например, t-критерий перестановки) требуют равной дисперсии при условии нормальности. В этом отношении классический перестановочный t-критерий имеет ту же слабость, что и классический t-критерий Стьюдента ( проблема Беренса-Фишера ). Эту проблему можно решить так же, как классический t-критерий был расширен для обработки неравных дисперсий: используя статистику Уэлча с поправкой Саттертуэйта на степени свободы. ^[6] Третьей альтернативой в этой ситуации является использование теста на основе начальной загрузки. Статистик Филип Гуд объясняет разницу между тестами перестановок и бутстрап-тестами следующим образом: «Перестановки проверяют гипотезы, касающиеся распределений; бутстрапы проверяют гипотезы, касающиеся параметров. В результате бутстрап влечет за собой менее строгие предположения». ^[7] Бутстрап-тесты неточны. В некоторых случаях тест на перестановку, основанный на правильно стьюдентизированной статистике, может быть асимптотически точным, даже если предположение об обменности нарушается. ^[8] Тесты на основе начальной загрузки могут проверять нулевую гипотезу и, следовательно, подходят для проведения тестирования эквивалентности . ${\displaystyle H_{0}:F\neq G}$

Тестирование Монте-Карло

Асимптотически эквивалентный тест на перестановку можно создать, когда существует слишком много возможных упорядочений данных, чтобы можно было выполнить полный перебор удобным способом. Это делается путем создания эталонного распределения методом выборки Монте-Карло , которая берет небольшую (относительно общего числа перестановок) случайную выборку из возможных повторов. Осознание того, что это можно применить к любому перестановочному тесту в любом наборе данных, стало важным прорывом в области прикладной статистики. Самые ранние известные ссылки на этот подход — Иден и Йейтс (1933) и Двасс (1957). ^{[9] [10]} Этот тип теста на перестановку известен под разными названиями: тест на приблизительную перестановку , тест на перестановку Монте-Карло или тест на случайную перестановку . ^[11]

После случайных перестановок можно получить доверительный интервал для значения p на основе биномиального распределения, см. Доверительный интервал биномиальной пропорции . Например, если после случайных перестановок значение p оценивается как , то 99% доверительный интервал для истины (тот, который возникнет в результате перебора всех возможных перестановок) равен . ${\displaystyle N}$ ${\displaystyle N=10000}$ ${\displaystyle {\widehat {p}}=0.05}$ ${\displaystyle p}$ ${\displaystyle \left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]}$

С другой стороны, цель оценки p-значения чаще всего состоит в том, чтобы решить , где находится порог, при котором нулевая гипотеза будет отклонена (обычно ). В приведенном выше примере доверительный интервал говорит нам только о том, что существует примерно 50% вероятность того, что значение p меньше 0,05, т.е. совершенно неясно, следует ли отклонять нулевую гипотезу на уровне . ${\displaystyle p\leq \alpha }$ ${\displaystyle \scriptstyle \ \alpha }$ ${\displaystyle \alpha =0.05}$ ${\displaystyle \alpha =0.05}$

Если важно только знать, является ли данное утверждение , логично продолжать моделирование до тех пор, пока не будет установлено, что утверждение истинно или ложно с очень низкой вероятностью ошибки. Учитывая границу допустимой вероятности ошибки (вероятность обнаружения того, что на самом деле или наоборот), вопрос о том, сколько перестановок сгенерировать, можно рассматривать как вопрос о том, когда прекратить генерировать перестановки, основываясь на результатах моделирования до сих пор, чтобы гарантировать, что вывод (или или ) верен с вероятностью, по крайней мере, такой же большой, как . ( обычно выбирается чрезвычайно малым, например, 1/1000.) Для достижения этого были разработаны правила остановки ^[12] , которые можно внедрить с минимальными дополнительными вычислительными затратами. Фактически, в зависимости от истинного базового значения p, часто оказывается, что количество требуемых симуляций чрезвычайно мало (например, всего 5, но часто не превышает 100), прежде чем решение может быть принято с виртуальной уверенностью. ${\displaystyle p\leq \alpha }$ ${\displaystyle \alpha }$ ${\displaystyle p\leq \alpha }$ ${\displaystyle \epsilon }$ ${\displaystyle {\widehat {p}}>\alpha }$ ${\displaystyle p\leq \alpha }$ ${\displaystyle p\leq \alpha }$ ${\displaystyle p>\alpha }$ ${\displaystyle 1-\epsilon }$ ${\displaystyle \epsilon }$

Примеры тестов

• Перестановочный анализ дисперсии
• Рейтинг продукта

Смотрите также

• Ранговый тест
• тест Лепажа

Литература

Оригинальные ссылки:

• Фишер, Р.А. (1935) План экспериментов , Нью-Йорк: Хафнер
• Питман, EJG (1937) «Тесты значимости, которые можно применять к выборкам из любой популяции», Приложение Королевского статистического общества , 4: 119–130 и 225–32 (части I и II). JSTOR  2984124 JSTOR  2983647
• Питман, EJG (1938). «Критерии значимости, которые можно применять к выборкам из любой совокупности. Часть III. Критерий дисперсионного анализа». Биометрика . 29 (3–4): 322–335. дои : 10.1093/biomet/29.3-4.322.

Современные ссылки:

• Коллингридж, DS (2013). «Букварь по квантовому анализу данных и тестированию перестановок». Журнал исследований смешанных методов . 7 (1): 79–95. дои : 10.1177/1558689812454457. S2CID  124618343.
• Эджингтон, Э.С., и Онгена, П. (2007) Рандомизационные тесты , 4-е изд. Нью-Йорк: Чепмен и Холл / ISBN CRC 9780367577711 
• Гуд, Филипп И. (2005) Перестановочные, параметрические и бутстреп-тесты гипотез , 3-е изд., Springer ISBN 0-387-98898-X 
• Хорошо, П. (2002). «Расширения понятия взаимозаменяемости и их приложения». Журнал современных прикладных статистических методов . 1 (2): 243–247. дои : 10.22237/jmasm/1036110240 .
• Луннеборг, Клифф. (1999) Анализ данных путем повторной выборки , Duxbury Press. ISBN 0-534-22110-6 . 
• Пезарин, Ф. (2001). Многомерные перестановочные тесты: с приложениями в биостатистике , John Wiley & Sons . ISBN 978-0471496700 
• Уэлч, WJ (1990). «Построение перестановочных тестов». Журнал Американской статистической ассоциации . 85 (411): 693–698. дои : 10.1080/01621459.1990.10474929.

Вычислительные методы:

• Мехта, ЧР; Патель, НР (1983). «Сетевой алгоритм для выполнения точного теста Фишера в таблицах непредвиденных обстоятельств rxc». Журнал Американской статистической ассоциации . 78 (382): 427–434. дои : 10.1080/01621459.1983.10477989.
• Мехта, ЧР; Патель, Северная Каролина; Сенчаудхури, П. (1988). «Выборка по важности для оценки точных вероятностей в перестановочном выводе». Журнал Американской статистической ассоциации . 83 (404): 999–1005. дои : 10.1080/01621459.1988.10478691.
• Гилл, PMW (2007). «Эффективный расчет p-значений в тестах значимости линейной статистики» (PDF) . Журнал статистических вычислений и моделирования . 77 (1): 55–61. CiteSeerX  10.1.1.708.1957 . дои : 10.1080/10629360500108053. S2CID  1813706.

Текущие исследования тестов на перестановку

• Гуд, ПИ (2012) Руководство для практикующих специалистов по методам повторной выборки.
• Гуд, ПИ (2005) Перестановочные, параметрические и бутстреп-тесты гипотез
• Хестерберг, Т.К., Д.С. Мур, С. Монаган, А. Клипсон и Р. Эпштейн (2005): Методы начальной загрузки и тесты перестановок, программное обеспечение.
• Мур, Д.С., Г. Маккейб, В. Дакворт и С. Склов (2003): Методы начальной загрузки и тесты перестановок
• Саймон, Дж. Л. (1997): Передискретизация: новая статистика.
• Ю, Чонг Хо (2003): Методы повторной выборки: концепции, приложения и обоснование. Практическая оценка, исследования и оценка, 8(19). (статистическая загрузка)
• Передискретизация: союз компьютеров и статистики (дайджесты ERIC)
• Пезарин Ф., Салмасо Л. (2010). Тесты перестановки сложных данных: теория, приложения и программное обеспечение. Уайли. https://www.google.de/books/edition/Permutation_Tests_for_Complex_Data/9PWVTOanxPUC?hl=de

Рекомендации

1. Мур, Джейсон Х. «Начальная настройка, тестирование перестановок и метод суррогатных данных». Физика в медицине и биологии 44.6 (1999): L11.
2. Онгена, Патрик (30 октября 2017 г.), Бергер, Вэнс В. (ред.), «Тесты рандомизации или тесты перестановки? Историческое и терминологическое уточнение», Рандомизация, маскирование и сокрытие распределения (1-е изд.), Бока Ратон, Флорида: Чепмен и Холл/CRC, стр. 209–228, номер документа : 10.1201/9781315305110-14, ISBN. 978-1-315-30511-0, получено 8 октября 2021 г.
3. Фипсон, Белинда; Смит, Гордон К. (2010). «P-значения перестановок никогда не должны быть равны нулю: вычисление точных p-значений, когда перестановки выбираются случайным образом». Статистические приложения в генетике и молекулярной биологии . 9 (1): Статья 39. arXiv : 1603.05766 . дои : 10.2202/1544-6115.1585. PMID  21044043. S2CID  10735784.
4. «Приглашенные статьи» (PDF) . Журнал современных прикладных статистических методов . 1 (2): 202–522. Осень 2011 г. Архивировано из оригинала (PDF) 5 мая 2003 г.
5. Коллингридж, Дэйв С. (11 сентября 2012 г.). «Букварь по квантовому анализу данных и тестированию перестановок». Журнал исследований смешанных методов . 7 (1): 81–97. дои : 10.1177/1558689812454457. S2CID  124618343.
6. Янссен, Арнольд (1997). «Студентизированные тесты перестановок для гипотез, не связанных с Iid, и обобщенная проблема Беренса-Фишера». Статистика и вероятностные буквы . 36 (1): 9–21. дои : 10.1016/s0167-7152(97)00043-6.
7. Хорошо, Филипп И. (2005). Методы повторной выборки: Практическое руководство по анализу данных (3-е изд.). Биркхойзер. ISBN 978-0817643867.
8. Чунг, EY; Романо, JP (2013). «Точные и асимптотически надежные тесты перестановок». Анналы статистики . 41 (2): 487–507. arXiv : 1304.5939 . дои : 10.1214/13-AOS1090 .
9. Иден, Т; Йейтс, Ф. (1933). «О достоверности z-критерия Фишера применительно к реальному примеру аномальных данных. (С пятью текстовыми цифрами)». Журнал сельскохозяйственной науки . 23 (1): 6–17. дои : 10.1017/S0021859600052862. S2CID  84802682 . Проверено 3 июня 2021 г.
10. Двасс, Мейер (1957). «Модифицированные тесты рандомизации для непараметрических гипотез». Анналы математической статистики . 28 (1): 181–187. дои : 10.1214/aoms/1177707045 . JSTOR  2237031.
11. Томас Э. Николс , Эндрю П. Холмс (2001). «Непараметрические перестановочные тесты для функциональной нейровизуализации: учебник с примерами» (PDF) . Картирование человеческого мозга . 15 (1): 1–25. дои : 10.1002/hbm.1058. hdl : 2027.42/35194. ПМК 6871862 . ПМИД  11747097. 
12. Ганди, Аксель (2009). «Последовательная реализация тестов Монте-Карло с равномерно ограниченным риском повторной выборки». Журнал Американской статистической ассоциации . 104 (488): 1504–1511. arXiv : math/0612488 . дои : 10.1198/jasa.2009.tm08368. S2CID  15935787.