В компьютерных сетях гиперкубические сети представляют собой тип сетевой топологии , используемый для соединения и маршрутизации данных между несколькими процессорами или компьютерами. Гиперкубические сети состоят из 2 m узлов , которые образуют вершины квадратов для создания межсетевого соединения. Гиперкуб по сути является многомерной ячеистой сетью с двумя узлами в каждом измерении. Из-за сходства такие топологии обычно группируются в k -арное d -мерное семейство ячеистых топологий, где d представляет собой число измерений, а k представляет собой число узлов в каждом измерении. [1]
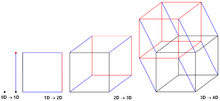
Сеть гиперкубических взаимосвязей формируется путем соединения N узлов, которые можно выразить как степень числа 2. Это означает, что если сеть имеет N узлов, ее можно выразить как:
где m — количество битов, необходимых для маркировки узлов в сети. Таким образом, если в сети 4 узла, для представления всех узлов в сети требуется 2 бита . Сеть строится путем соединения узлов, которые отличаются только одним битом в своем двоичном представлении. Это обычно называется двоичной маркировкой. Объединенная сеть трехмерного гиперкуба будет представлять собой куб с 8 узлами и 12 ребрами . Сеть четырехмерного гиперкуба может быть создана путем дублирования двух трехмерных сетей и добавления старшего бита. Новый добавленный бит должен быть «0» для одного трехмерного гиперкуба и «1» для другого трехмерного гиперкуба. Углы соответствующих однобитно измененных старших битов соединяются для создания более высокой сети гиперкуба. Этот метод можно использовать для построения любого гиперкуба, представленного m-битом, с гиперкубом, представленным (m-1)-битом. [2]
Метод маршрутизации для сети гиперкуба называется маршрутизацией E-Cube. Расстояние между двумя узлами в сети может быть задано весом Хэмминга (числом единиц в) операции XOR между их соответствующими бинарными метками.
Расстояние между узлом 1 (обозначенным как «01») и узлом 2 (обозначенным как «10») в сети определяется по формуле:
Маршрутизация E-Cube — это метод статической маршрутизации , использующий алгоритм XY-маршрутизации . Обычно это называют детерминированной моделью маршрутизации с упорядоченным измерением . Маршрутизация E-Cube работает путем обхода сети в k-м измерении , где k — младший ненулевой бит в результате вычисления расстояния.
Например, пусть метка отправителя будет «00», а метка получателя — «11». Таким образом, расстояние между ними равно 11, а младший ненулевой бит — это бит LSB . Определение того, в какую сторону идти для «0» или «1», определяется алгоритмом маршрутизации XY. [3]
Для оценки эффективности сетевого соединения гиперкуба по сравнению с другими топологиями сетей используются различные показатели производительности. [ неопределенно ]
Это определяет количество непосредственно смежных узлов к конкретному узлу. Эти узлы должны быть непосредственными соседями. В случае гиперкуба степень равна m.
Это определяет максимальное количество узлов, через которые должно пройти сообщение на своем пути от источника к месту назначения. Это в основном дает нам задержку при передаче сообщения по сети. В случае гиперкуба диаметр равен m.
Расстояние между двумя узлами, определяемое числом переходов в кратчайшем пути между двумя конкретными узлами. Оно задается формулой -
В случае гиперкубов среднее расстояние указывается как м/2.
Это наименьшее количество проводов, которое нужно перерезать, чтобы разделить сеть на две равные половины. Для гиперкубов оно равно 2 м-1 . [1]