Мгновенный центр вращения

Точка, прикрепленная к телу, совершающему плоское движение

Рисунок 1: Мгновенный центр P движущейся плоскости

Мгновенный центр вращения (также известный как мгновенный центр скорости , ^[1] мгновенный центр или полюс плоского смещения ) тела, совершающего плоское движение, — это точка, имеющая нулевую скорость в определенный момент времени. В этот момент векторы скорости других точек тела создают круговое поле вокруг этого центра вращения , которое идентично тому, что создается чистым вращением .

Плоское движение тела часто описывается с помощью плоской фигуры, движущейся в двумерной плоскости . Мгновенный центр — это точка в движущейся плоскости, вокруг которой вращаются все остальные точки в определенный момент времени.

Непрерывное движение плоскости имеет мгновенный центр для каждого значения параметра времени. Это порождает кривую, называемую движущимся центроидом . Точки в неподвижной плоскости, соответствующие этим мгновенным центрам, образуют неподвижный центроид.

Обобщение этой концепции на трехмерное пространство — это закручивание вокруг винта. Винт имеет ось, которая является линией в трехмерном пространстве (не обязательно через начало координат), ось вращения ; винт также имеет конечный шаг (фиксированное перемещение вдоль своей оси, соответствующее вращению вокруг оси винта).

Полюс плоского смещения

Рисунок 2: Полюс плоского смещения

Мгновенный центр можно считать предельным случаем полюса плоского смещения.

Плоское перемещение тела из положения 1 в положение 2 определяется комбинацией плоского вращения и плоской трансляции . Для любого плоского перемещения существует точка в движущемся теле, которая находится в одном и том же месте до и после перемещения. Смещение можно рассматривать как вращение вокруг этого полюса.

Построение полюса плоского смещения

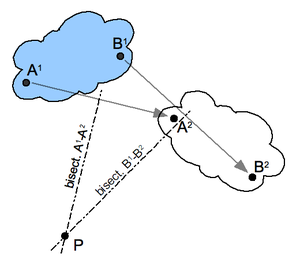
Сначала выберите две точки A и B в движущемся теле и найдите соответствующие точки в двух положениях; см. иллюстрацию. Постройте перпендикулярные серединные линии к двум отрезкам A ¹ A ² и B ¹ B ² . Пересечение P этих двух биссектрис является полюсом плоского смещения. Обратите внимание, что A ¹ и A ² лежат на окружности вокруг P. Это справедливо для соответствующих положений каждой точки в теле.

Если два положения тела разделены моментом времени в плоском движении, то полюс перемещения становится мгновенным центром. В этом случае отрезки, построенные между мгновенными положениями точек A и B, становятся векторами скорости V _A и V _B . Прямые, перпендикулярные этим векторам скорости, пересекаются в мгновенном центре.

Алгебраическую конструкцию декартовых координат можно организовать следующим образом: средняя точка между и имеет декартовы координаты ${\displaystyle \left(P_{x},P_{y}\right)}$ ${\displaystyle A^{1}}$ ${\displaystyle A^{2}}$

${\displaystyle A_{x}^{m}={\frac {1}{2}}\left(A_{x}^{1}+A_{x}^{2}\right);\quad A_{y}^{m}={\frac {1}{2}}\left(A_{y}^{1}+A_{y}^{2}\right),}$

а средняя точка между и имеет декартовы координаты ${\displaystyle B^{1}}$ ${\displaystyle B^{2}}$

${\displaystyle B_{x}^{m}={\frac {1}{2}}\left(B_{x}^{1}+B_{x}^{2}\right);\quad B_{y}^{m}={\frac {1}{2}}\left(B_{y}^{1}+B_{y}^{2}\right).}$

Два угла от до и от до, измеренные против часовой стрелки относительно горизонтали, определяются по формуле ${\displaystyle A^{1}}$ ${\displaystyle A^{2}}$ ${\displaystyle B^{1}}$ ${\displaystyle B^{2}}$

${\displaystyle \tan \tau _{A}={\frac {A_{y}^{2}-A_{y}^{1}}{A_{x}^{2}-A_{x}^{1}}},\quad \tan \tau _{B}={\frac {B_{y}^{2}-B_{y}^{1}}{B_{x}^{2}-B_{x}^{1}}}}$

Найдите положение ${\displaystyle P\left(P_{x},P_{y}\right)}$

Метод 1:

Взяв правильные ветви касательной . Пусть центр вращения имеет расстояния и до двух средних точек. Предполагая вращение по часовой стрелке (иначе поменяйте знак ): ${\displaystyle \left(P_{x},P_{y}\right)}$ ${\displaystyle d_{A}}$ ${\displaystyle d_{B}}$ ${\displaystyle \pi /2}$

${\displaystyle {\begin{aligned}P_{x}&=A_{x}^{m}+d_{A}\cos \left(\tau _{A}-{\frac {\pi }{2}}\right)\\&=B_{x}^{m}+d_{B}\cos \left(\tau _{B}-{\frac {\pi }{2}}\right);\\P_{y}&=A_{y}^{m}+d_{A}\sin \left(\tau _{A}-{\frac {\pi }{2}}\right)\\&=B_{y}^{m}+d_{B}\sin \left(\tau _{B}-{\frac {\pi }{2}}\right).\end{aligned}}}$

Перепишем это как неоднородную систему линейных уравнений 4 × 4 с 4 неизвестными (два расстояния и две координаты центра): ${\displaystyle d}$ ${\displaystyle P}$

${\displaystyle {\begin{pmatrix}1&0&-\sin \tau _{A}&0\\1&0&0&-\sin \tau _{B}\\0&1&\cos \tau _{A}&0\\0&1&0&\cos \tau _{B}\end{pmatrix}}{\begin{pmatrix}P_{x}\\P_{y}\\d_{A}\\d_{B}\end{pmatrix}}={\begin{pmatrix}A_{x}^{m}\\B_{x}^{m}\\A_{y}^{m}\\B_{y}^{m}\end{pmatrix}}.}$

Координаты центра вращения — первые две компоненты вектора решения

${\displaystyle {\begin{pmatrix}P_{x}\\P_{y}\\d_{A}\\d_{B}\end{pmatrix}}={\frac {1}{\sin \left(\tau _{A}-\tau _{B}\right)}}{\begin{pmatrix}\left(B_{y}^{m}-A_{y}^{m}\right)\sin \tau _{A}\sin \tau _{B}+B_{x}^{m}\sin \tau _{A}\cos \tau _{B}-A_{x}^{m}\cos \tau _{A}\sin \tau _{B}\\\left(A_{x}^{m}-B_{x}^{m}\right)\cos \tau _{A}\cos \tau _{B}+A_{y}^{m}\sin \tau _{A}\cos \tau _{B}-B_{y}^{m}\cos \tau _{A}\sin \tau _{B}\\\left(B_{x}^{m}-A_{x}^{m}\right)\cos \tau _{B}+\left(B_{y}^{m}-A_{y}^{m}\right)\sin \tau _{B}\\\left(B_{x}^{m}-A_{x}^{m}\right)\cos \tau _{A}+\left(B_{y}^{m}-A_{y}^{m}\right)\sin \tau _{A}\\\end{pmatrix}}.}$

Метод 2:

Найдите уравнения биссектрис двух отрезков A ¹ A ² и B ¹ B ² следующим образом:

Уравнение прямой линии в форме точки-наклона имеет вид: где — точка, а — наклон. ${\displaystyle y-y_{0}=m(x-x_{0})}$ ${\displaystyle (x_{0},y_{0})}$ ${\displaystyle m}$

Уравнение биссектрисы треугольника A ¹ A ² имеет вид ${\displaystyle y-A_{y}^{m}=\tan \tau _{A}\left(x-A_{x}^{m}\right)}$

Уравнение биссектрисы B ¹ B ² имеет вид ${\displaystyle y-B_{y}^{m}=\tan \tau _{B}\left(x-B_{x}^{m}\right)}$

Эти две биссектрисы пересекаются, поэтому можно записать систему из 2 уравнений с 2 ​​неизвестными и коэффициентами ${\displaystyle P\left(P_{x},P_{y}\right)}$

${\displaystyle {\begin{cases}P_{y}-A_{y}^{m}=\tan \tau _{A}\left(P_{x}-A_{x}^{m}\right)\\P_{y}-B_{y}^{m}=\tan \tau _{B}\left(P_{x}-B_{x}^{m}\right)\end{cases}}}$

Решение этой системы:

${\displaystyle P_{x}={\frac {B_{y}^{m}-A_{y}^{m}+A_{x}^{m}\tan \tau _{A}-B_{x}^{m}\tan \tau _{B}}{\tan \tau _{A}-\tan \tau _{B}}},\qquad P_{y}={\frac {B_{y}^{m}-A_{y}^{m}+\tan \tau _{A}\left(A_{x}^{m}-B_{x}^{m}\right)}{\tan \tau _{A}-\tan \tau _{B}}}+B_{y}^{m}}$

Чистый перевод

Если смещение между двумя положениями является чистым переносом, то перпендикуляры, проведенные через серединные отрезки A ¹ B ¹ и A ² B ^2, образуют параллельные прямые. Считается, что эти прямые пересекаются в точке на бесконечности , поэтому говорят, что полюс этого плоского смещения «лежит в бесконечности» в направлении перпендикуляров, проведенных через серединные отрезки.

В пределе чистое перемещение становится плоским движением с параллельными векторами скорости точек. В этом случае говорят, что мгновенный центр лежит на бесконечности в направлении, перпендикулярном векторам скорости.

Мгновенный центр колеса, катящегося без проскальзывания

Эскиз 3: Вращающееся колесо.

Мгновенный центр вращения катящегося колеса, разбитый на точки. Разбив катящееся колесо на несколько точек, можно легче увидеть, как все точки колеса вращаются вокруг одной точки в каждый момент времени. Эта точка является мгновенным центром вращения, показанным черным цветом.

Рассмотрим плоское движение круглого колеса, катящегося без проскальзывания по линейной дороге; см. рисунок 3. Колесо вращается вокруг своей оси M, которая перемещается в направлении, параллельном дороге. Точка контакта P колеса с дорогой не проскальзывает, что означает, что точка P имеет нулевую скорость относительно дороги. Таким образом, в момент, когда точка P на колесе соприкасается с дорогой, она мгновенно становится центром.

Множество точек движущегося колеса, которые становятся мгновенными центрами, — это сама окружность, которая определяет движущийся центроид. Точки в неподвижной плоскости, которые соответствуют этим мгновенным центрам, — это линия дороги, которая определяет неподвижный центроид.

Вектор скорости точки A в колесе перпендикулярен отрезку AP и пропорционален длине этого отрезка. В частности, скорости точек в колесе определяются угловой скоростью вращения колеса вокруг P. Векторы скорости ряда точек показаны на рисунке 3 и могут быть рассчитаны с помощью следующего уравнения:

${\displaystyle {\vec {v}}={\vec {\omega }}\times {\vec {r}}_{A}}$

где - скорость точки А, угловая скорость колеса и вектор из точки Р в А. ${\displaystyle {\vec {v}}}$ ${\displaystyle {\vec {\omega }}}$ ${\displaystyle {\vec {r}}_{A}}$

Чем дальше точка в колесе от мгновенного центра P, тем пропорционально больше ее скорость. Таким образом, точка наверху колеса движется в том же направлении, что и центр M колеса, но в два раза быстрее, так как она находится на вдвое большем расстоянии от P. Все точки, которые находятся на расстоянии, равном радиусу колеса 'r' от точки P, движутся с той же скоростью, что и точка M, но в разных направлениях. Это показано для точки на колесе, которая имеет ту же скорость, что и M, но движется в направлении, касательном к окружности вокруг P.

Относительный центр вращения двух соприкасающихся плоских тел

Рисунок 4: Пример относительного центра вращения. Два тела, соприкасающиеся в точке C , одно из которых вращается вокруг точки A , а другое вокруг точки B, должны иметь относительный центр вращения где-то вдоль линии AB . Поскольку части не могут проникать друг в друга, относительный центр вращения также должен быть вдоль нормального направления к контакту и через точку C. Единственное возможное решение — если относительный центр находится в точке D.

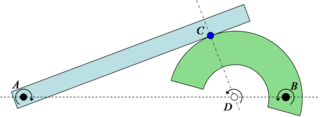
Если два плоских твердых тела находятся в контакте, и каждое тело имеет свой собственный центр вращения, то относительный центр вращения между телами должен лежать где-то на линии, соединяющей два центра. В результате, поскольку чистое качение может существовать только тогда, когда центр вращения находится в точке контакта (как показано выше с колесом на дороге), чистое качение может быть достигнуто только тогда, когда точка контакта проходит через линию, соединяющую два центра вращения. Это известно в конструкции эвольвентной передачи как точка шага, где нет относительного скольжения между шестернями. Фактически, передаточное отношение между двумя вращающимися частями находится по отношению двух расстояний до относительного центра. В примере на рисунке 4 передаточное отношение равно ${\displaystyle \gamma ={\frac {AD}{BD}}}$

Мгновенный центр вращения и механизмы

На рисунке 1 выше показан четырехзвенный шарнир , где проиллюстрирован ряд мгновенных центров вращения. Жесткое тело, обозначенное буквами BAC, соединено с основанием или рамой с помощью звеньев P ₁ -A и P _{2 -B.}

Три подвижные части этого механизма (основание неподвижно): звено P ₁ -A, звено P ₂ -B и корпус BAC. Для каждой из этих трех частей можно определить мгновенный центр вращения.

Рассмотрим первое звено P ₁ -A: все точки этого звена, включая точку A, вращаются вокруг точки P ₁ . Поскольку P ₁ является единственной точкой, не движущейся в данной плоскости, ее можно назвать мгновенным центром вращения для этого звена. Точка A, находящаяся на расстоянии P ₁ -A от P ₁ , движется по окружности в направлении, перпендикулярном звену P ₁ -A, как указано вектором V _A .

То же самое относится к звену P ₂ -B: точка P ₂ является мгновенным центром вращения этого звена, а точка B движется в направлении, указанном вектором V _B .

Для определения мгновенного центра вращения третьего элемента рычажной передачи, тела BAC, используются две точки A и B, поскольку его подвижные характеристики известны, поскольку выводятся из информации о звеньях P ₁ -A и P ₂ -B.

Направление скорости точки A указывается вектором V _A . Ее мгновенный центр вращения должен быть перпендикулярен этому вектору (так как V _A расположен по касательной к окружности). Единственная линия, которая удовлетворяет требованию, — это линия, коллинеарная со связью P ₁ -A. Где-то на этой линии находится точка P, мгновенный центр вращения для тела BAC.

То, что применимо к точке A, применимо и к точке B, поэтому этот мгновенный центр вращения P расположен на линии, перпендикулярной вектору V _B , линии, коллинеарной со связью P ₂ - B. Следовательно, мгновенный центр вращения P тела BAC находится в точке пересечения прямых, проходящих через P ₁ -A и P ₂ -B.

Поскольку этот мгновенный центр вращения P является центром для всех точек тела BAC для любой случайной точки, скажем, точки C, скорость и направление движения можно определить: соедините P с C. Направление движения точки C перпендикулярно этому соединению. Скорость пропорциональна расстоянию до точки P.

Продолжая этот подход с двумя звеньями P ₁ -A и P ₂ -B, вращающимися вокруг своих собственных мгновенных центров вращения, можно определить центроид для мгновенного центра вращения P. Из этого можно определить путь движения для C или любой другой точки на теле BAC.

Примеры применения

В биомеханических исследованиях мгновенный центр вращения наблюдается для функционирования суставов верхних и нижних конечностей. ^[2] Например, при анализе коленного , [ ^{3] [4] [5]} голеностопного , ^[6] или плечевого суставов. ^{[7] [8]} Такие знания помогают в разработке искусственных суставов и протезов , таких как локтевые ^[9] или суставы пальцев. ^[10]

Исследование суставов лошадей: «...векторы скорости, определенные из мгновенных центров вращения, показали, что поверхности суставов скользят друг по другу» ^[11].

Исследования по повороту судна, движущегося по воде. ^[12]

Тормозные характеристики автомобиля можно улучшить, изменив конструкцию механизма педали тормоза. [ ^13]

Проектирование подвески велосипеда ^[14] или автомобиля ^{[15] .}

В случае звена сцепки в четырехзвенной рычажной передаче , например , подвеска с двойным поперечным рычагом спереди, перпендикуляры к скорости лежат вдоль звеньев, соединяющих заземленное звено с звеном сцепки. Такая конструкция используется для установления кинематического центра крена подвески.

Смотрите также

• Угловая скорость
• Теория Берместера
• Центрод
• Группа точечного отражения
• Твёрдое тело
• Центр рулона
• Вращение вокруг фиксированной оси
• Ось винта
• Двумерное вращение

Ссылки

1. Иллюстрированный словарь по машиностроению: английский, немецкий, французский, голландский, русский (Springer Science & Business Media, 17 апреля 2013 г. - 422 страницы)
2. "Физиология мышц — момент силы в суставе". Архивировано из оригинала 2021-02-27 . Получено 2008-08-22 .
3. Описание и измерение движения коленного сустава ^{[ постоянная мертвая ссылка ]}
4. Moorehead JD, Montgomery SC, Harvey DM (сентябрь 2003 г.). «Мгновенная оценка центра вращения с использованием техники Reuleaux и техники боковой экстраполяции». J Biomech . 36 (9): 1301–7. doi :10.1016/S0021-9290(03)00156-8. PMID  12893038.
5. Hollman JH, Deusinger RH, Van Dillen LR, Matava MJ (август 2003 г.). «Гендерные различия в поверхностной качения и скользящей кинематике колена». Clin Orthop Relat Res . 413 (413): 208–21. doi :10.1097/01.blo.0000072902.36018.fe. PMID  12897612. S2CID  45191914.
6. Maganaris CN, Baltzopoulos V, Sargeant AJ (август 1998 г.). «Изменения в плече момента ахиллова сухожилия от покоя до максимального изометрического сгибания подошвы: наблюдения in vivo у человека». Journal of Physiology . 510 (Pt 3): 977–85. doi :10.1111/j.1469-7793.1998.977bj.x. PMC 2231068 . PMID  9660906. Архивировано из оригинала 2012-09-08. 
7. Биомеханика плеча ^{[ постоянная мертвая ссылка ]}
8. Poppen NK, Walker PS (март 1976). «Нормальное и ненормальное движение плеча». J Bone Joint Surg Am . 58 (2): 195–201. doi :10.2106/00004623-197658020-00006. PMID  1254624.
9. US 5030237  Протез локтевого сустава
10. "Pyrocarbon Finger Joint Implant" (PDF) . Архивировано из оригинала (PDF) 2011-07-21 . Получено 2008-08-22 .
11. Колахан П., Пиотровски Г., Пулос П. (сентябрь 1988 г.). «Кинематический анализ мгновенных центров вращения пястно-фалангового сустава лошади». Am J Vet Res . 49 (9): 1560–5. PMID  3223666.
12. "ЧАСТЬ VI Навигация и маневрирование судов" (PDF) . Архивировано из оригинала (PDF) 2009-12-15 . Получено 2008-08-22 .
13. GB 1443270 Крепления педали тормоза с переменным механическим передаточным отношением - General Motors, 1976 
14. US 7100930 Система задней подвески велосипеда 
15. Реза Н. Джазар (2008). Динамика транспортных средств: теория и применение. Берлин: Springer. ISBN 978-0-387-74243-4.