В механике чистая сила — это сумма всех сил, действующих на объект. Например, если две силы действуют на объект в противоположных направлениях, и одна сила больше другой, то силы можно заменить одной силой, которая является разностью большей и меньшей силы. Эта сила и есть чистая сила. [1]
Когда силы действуют на объект, они изменяют его ускорение . Чистая сила — это совокупное воздействие всех сил на ускорение объекта, как описано вторым законом движения Ньютона .
Когда чистая сила прикладывается к определенной точке объекта, можно рассчитать связанный с ней крутящий момент . Сумма чистой силы и крутящего момента называется результирующей силой , которая заставляет объект вращаться так же, как если бы все силы, действующие на него, применялись по отдельности. [2]
Возможно, что все силы, действующие на объект, не создают вообще никакого крутящего момента. Это происходит, когда чистая сила прикладывается вдоль линии действия .
В некоторых текстах термины результирующая сила и чистая сила используются так, как будто они означают одно и то же. Это не всегда так, особенно в сложных темах, таких как движение вращающихся объектов или ситуации, когда все идеально сбалансировано, известные как статическое равновесие . В этих случаях важно понимать, что «чистая сила» и «результирующая сила» могут иметь разные значения.
В физике сила считается векторной величиной. Это означает, что она имеет не только размер (или величину), но и направление, в котором она действует. Обычно мы обозначаем силу жирным шрифтом F или иногда помещаем стрелку над символом, чтобы указать на ее векторную природу, например: .
Когда нам нужно визуально представить силу, мы рисуем отрезок линии. Этот отрезок начинается в точке A , где приложена сила, и заканчивается в другой точке B. Эта линия не только дает нам направление силы (от A до B ), но и ее величину: чем длиннее линия, тем больше сила.
Одной из основных концепций в физике является то, что силы можно складывать, что является основой векторного сложения. Эта концепция была центральной в физике со времен Галилея и Ньютона, формируя краеугольный камень векторного исчисления , которое стало самостоятельным в конце 1800-х и начале 1900-х годов. [3]
На рисунке справа показано, как сложить две силы, используя метод «кончик-к-хвосту». Этот метод включает в себя рисование сил , и от кончика первой силы. Результирующая сила, или «общая» сила, , затем рисуется от начала первой силы (хвоста) до конца второй силы (кончика). Понимание этой концепции имеет основополагающее значение для понимания того, как силы взаимодействуют и объединяются, чтобы влиять на движение и равновесие объектов.
Когда силы прикладываются к протяженному телу (телу, которое не является одной точкой), они могут быть приложены в разных точках. Такие силы называются «связанными векторами». Важно помнить, что для сложения этих сил их нужно рассматривать в одной и той же точке.
Концепция «чистой силы» вступает в игру, когда вы смотрите на общее воздействие всех этих сил на тело. Однако чистая сила сама по себе не обязательно сохраняет движение тела. Это происходит потому, что, помимо чистой силы, «крутящий момент» или вращательный эффект, связанный с этими силами, также имеет значение. Чистая сила должна быть приложена в правильной точке и с правильным связанным крутящим моментом, чтобы воспроизвести воздействие исходных сил.
Когда чистая сила и соответствующий крутящий момент прикладываются в одной точке, они вместе составляют то, что известно как результирующая сила . Эта результирующая комбинация силы и крутящего момента будет иметь такое же воздействие на тело, как и все исходные силы и связанные с ними крутящие моменты.
Сила известна как связанный вектор — это означает, что она имеет направление, величину и точку приложения . Удобный способ определить силу — это отрезок прямой от точки A до точки B. Если обозначить координаты этих точек как A = (A x , A y , A z ) и B = (B x , B y , B z ), то вектор силы, приложенный в точке A, будет определяться как
Длина вектора определяет величину и задается выражением
Сумма двух сил F 1 и F 2 , приложенных в точке A, может быть вычислена из суммы определяющих их сегментов. Пусть F 1 = B − A и F 2 = D − A , тогда сумма этих двух векторов равна
что можно записать как
где E — середина отрезка BD , соединяющего точки B и D.
Таким образом, сумма сил F 1 и F 2 равна удвоенному отрезку, соединяющему точку A со средней точкой E отрезка, соединяющего конечные точки B и D двух сил. Удвоение этой длины легко достигается путем определения отрезков BC и DC , параллельных AD и AB , соответственно, чтобы завершить параллелограмм ABCD . Диагональ AC этого параллелограмма является суммой двух векторов сил. Это известно как правило параллелограмма для сложения сил.
Когда сила действует на частицу, она приложена к одной точке (объем частицы пренебрежимо мал): это точечная сила, а частица является точкой ее приложения. Но внешняя сила, действующая на протяженное тело (объект), может быть приложена к нескольким его составным частицам, т. е. может быть «распределена» по некоторому объему или поверхности тела. Однако для определения ее вращательного воздействия на тело необходимо указать ее точку приложения (фактически, линию приложения, как поясняется ниже). Обычно проблема решается следующими способами:
В любом случае анализ движения твердого тела начинается с модели точечной силы. И когда сила, действующая на тело, изображается графически, ориентированный отрезок линии, представляющий силу, обычно рисуется так, чтобы «начинаться» (или «заканчиваться») в точке приложения.

В примере, показанном на схеме напротив, на свободное твердое тело в точке приложения H действует одна сила . Тело имеет массу , а его центр масс находится в точке C. В приближении постоянной массы сила вызывает изменения в движении тела, описываемые следующими выражениями:
Во втором выражении — крутящий момент или момент силы, а — момент инерции тела. Крутящий момент, вызванный силой , — это векторная величина, определяемая относительно некоторой точки отсчета:
Вектор — это радиус-вектор точки приложения силы, и в этом примере он проведен из центра масс как отсчетной точки (см. диаграмму). Отрезок прямой линии — это плечо рычага силы относительно центра масс. Как следует из иллюстрации, крутящий момент не меняется (то же плечо рычага), если точка приложения перемещается вдоль линии приложения силы (пунктирная черная линия). Более формально это следует из свойств векторного произведения и показывает, что вращательный эффект силы зависит только от положения ее линии приложения, а не от конкретного выбора точки приложения вдоль этой линии.
Вектор крутящего момента перпендикулярен плоскости, определяемой силой и вектором , и в этом примере он направлен к наблюдателю; вектор углового ускорения имеет то же направление. Правило правой руки связывает это направление с вращением по часовой стрелке или против часовой стрелки в плоскости чертежа.
Момент инерции вычисляется относительно оси, проходящей через центр масс, параллельный крутящему моменту. Если тело, показанное на рисунке, представляет собой однородный диск, этот момент инерции равен . Если диск имеет массу 0,5 кг и радиус 0,8 м, момент инерции равен 0,16 кгм 2 . Если величина силы равна 2 Н, а плечо рычага 0,6 м, величина крутящего момента равна 1,2 Нм. В показанный момент сила сообщает диску угловое ускорение α = τ /I = 7,5 рад/с 2 , а его центру масс она сообщает линейное ускорение a = F / м = 4 м/с 2 .

Результирующая сила и крутящий момент заменяют эффекты системы сил, действующих на движение твердого тела. Интересным частным случаем является результирующая без крутящего момента, которая может быть найдена следующим образом:
где - чистая сила, - определяет ее точку приложения, а отдельные силы имеют точки приложения . Может оказаться, что нет точки приложения, которая дает равнодействующую без крутящего момента.
На схеме напротив показаны простые графические методы нахождения линии приложения равнодействующей силы простых плоских систем:
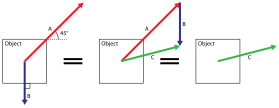
В общем случае систему сил, действующих на твердое тело, всегда можно заменить одной силой плюс одним чистым (см. предыдущий раздел) крутящим моментом. Сила является чистой силой, но для вычисления дополнительного крутящего момента чистой силе должна быть назначена линия действия. Линия действия может быть выбрана произвольно, но дополнительный чистый крутящий момент зависит от этого выбора. В частном случае можно найти такую линию действия, что этот дополнительный крутящий момент равен нулю.
Результирующая сила и крутящий момент могут быть определены для любой конфигурации сил. Однако интересным частным случаем является результирующая без крутящего момента. Это полезно как концептуально, так и практически, поскольку тело движется без вращения, как если бы оно было частицей.
Некоторые авторы не различают результирующую силу и чистую силу и используют эти термины как синонимы . [4]