Суд над Бернулли

Любой эксперимент с двумя возможными случайными исходами.

Графики вероятности P ненаблюдения независимых событий каждого из вероятностей p после n испытаний Бернулли в сравнении с np для различных p . Показаны три примера:
Синяя кривая : бросание шестигранного кубика 6 раз дает 33,5% вероятность того, что 6 (или любое другое заданное число) никогда не выпадет; можно заметить, что по мере увеличения n вероятность того, что 1/ n -случайное событие никогда не появится после n попыток, быстро стремится к 0 .
Серая кривая : чтобы получить шанс 50-50 выбросить Ятзи (5 кубических кубиков с одинаковым числом), требуется 0,69 × 1296 ~ 898 бросков.
Зеленая кривая : вытягивание карты из колоды игральных карт без джокеров 100 (1,92×52) раз с заменой дает 85,7% шанс вытянуть пиковый туз хотя бы один раз.

В теории вероятностей и статистике испытание Бернулли (или биномиальное испытание ) — это случайный эксперимент с ровно двумя возможными исходами : «успех» и «неудача», в котором вероятность успеха одинакова каждый раз, когда проводится эксперимент. ^[1] Он назван в честь Якоба Бернулли , швейцарского математика 17-го века, который проанализировал их в своей книге «Ars Conjectandi» (1713). ^[2]

Математическая формализация процесса Бернулли известна как процесс Бернулли . Эта статья предлагает элементарное введение в эту концепцию, тогда как статья о процессе Бернулли предлагает более продвинутое рассмотрение.

Поскольку испытание Бернулли имеет только два возможных результата, его можно сформулировать как вопрос «да или нет». Например:

• Является ли верхняя карта перетасованной колоды тузом?
• Был ли новорожденный ребенок девочкой? (См. соотношение полов у людей .)

Таким образом, успех и неудача — это просто обозначения этих двух результатов, и их не следует понимать буквально. Термин «успех» в этом смысле состоит в результате, удовлетворяющем заданным условиям; это не оценочное суждение. В более общем смысле, учитывая любое вероятностное пространство , для любого события (набора результатов) можно определить испытание Бернулли, соответствующее тому, произошло событие или нет (событие или дополнительное событие ). Примеры испытаний Бернулли включают:

• Подбрасывание монеты . В этом контексте аверс («орёл») традиционно обозначает успех, а реверс («решка») — неудачу. Честная монета по определению имеет вероятность успеха 0,5. В этом случае возможны ровно два исхода.
• Бросок кубика , где шестерка – «успех», а все остальное – «неудача». В этом случае существует шесть возможных исходов, а событие — шестеркой; дополнительное событие «не шестерка» соответствует остальным пяти возможным исходам.
• При проведении опроса политического мнения случайный выбор избирателя, чтобы выяснить, проголосует ли этот избиратель «за» на предстоящем референдуме.

Определение

Независимые повторные испытания эксперимента с ровно двумя возможными исходами называются испытаниями Бернулли. Назовите один из результатов «успехом», а другой — «неудачей». Пусть – вероятность успеха в испытании Бернулли, – вероятность неудачи. Тогда вероятность успеха и вероятность неудачи в сумме равны единице, поскольку это взаимодополняющие события: «успех» и «неудача» взаимоисключающие и исчерпывающие . Таким образом, возникают следующие отношения: ${\displaystyle p}$ ${\displaystyle q}$

${\displaystyle p=1-q,\quad \quad q=1-p,\quad \quad p+q=1.}$

В качестве альтернативы их можно выразить в терминах шансов : при заданной вероятности успеха и неудачи шансы на есть , а шансы против равны . Их также можно выразить в виде чисел путем деления, что дает шансы на и шансы против. : ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle p:q}$ ${\displaystyle q:p.}$ ${\displaystyle o_{f}}$ ${\displaystyle o_{a}}$

${\displaystyle {\begin{aligned}o_{f}&=p/q=p/(1-p)=(1-q)/q\\o_{a}&=q/p=(1-p)/p=q/(1-q).\end{aligned}}}$

Это мультипликативные обратные числа , поэтому они умножаются на 1 со следующими соотношениями:

${\displaystyle o_{f}=1/o_{a},\quad o_{a}=1/o_{f},\quad o_{f}\cdot o_{a}=1.}$

В случае, когда испытание Бернулли представляет собой событие из конечного числа равновероятных исходов , где исходами являются успех, а среди исходов - неудача, шансы за и шансы против равны. Это дает следующие формулы для вероятности и шансов: ${\displaystyle S}$ ${\displaystyle F}$ ${\displaystyle S:F}$ ${\displaystyle F:S.}$

${\displaystyle {\begin{aligned}p&=S/(S+F)\\q&=F/(S+F)\\o_{f}&=S/F\\o_{a}&=F/S.\end{aligned}}}$

Здесь шансы вычисляются путем деления количества исходов, а не вероятностей, но пропорция та же самая, поскольку эти отношения различаются только за счет умножения обоих членов на один и тот же постоянный коэффициент.

Случайные переменные , описывающие испытания Бернулли, часто кодируются по соглашению: 1 = «успех», 0 = «неуспех».

С испытанием Бернулли тесно связан биномиальный эксперимент, который состоит из фиксированного числа статистически независимых испытаний Бернулли, каждое из которых имеет вероятность успеха , и подсчитывает количество успехов. Случайная величина, соответствующая биномиальному эксперименту, обозначается и считается, что она имеет биномиальное распределение . Вероятность именно успеха в эксперименте определяется выражением: ${\displaystyle n}$ ${\displaystyle p}$ ${\displaystyle B(n,p)}$ ${\displaystyle k}$ ${\displaystyle B(n,p)}$

${\displaystyle P(k)={n \choose k}p^{k}q^{n-k}}$

где – биномиальный коэффициент . ${\displaystyle {n \choose k}}$

Испытания Бернулли могут также привести к отрицательным биномиальным распределениям (которые подсчитывают количество успехов в серии повторных испытаний Бернулли до тех пор, пока не будет обнаружено определенное количество неудач), а также к различным другим распределениям.

Когда выполняются несколько испытаний Бернулли, каждое из которых имеет свою вероятность успеха, их иногда называют испытаниями Пуассона . ^[3]

Пример: бросание монет.

Рассмотрим простой эксперимент, в котором честную монету подбрасывают четыре раза. Найти вероятность того, что ровно при двух бросках выпадет решка.

Решение

Представление возможных результатов четырехкратного подбрасывания честной монеты в зависимости от количества орлов. Как видно, вероятность выпадения ровно двух орлов за четыре броска равна 6/16 = 3/8, что соответствует расчетам.

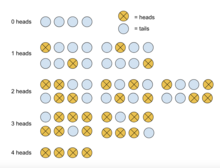
В этом эксперименте пусть орел будет определен как успех , а решка как неудача. Поскольку предполагается, что монета честная, вероятность успеха равна . Таким образом, вероятность отказа определяется выражением ${\displaystyle p={\tfrac {1}{2}}}$ ${\displaystyle q}$

${\displaystyle q=1-p=1-{\tfrac {1}{2}}={\tfrac {1}{2}}}$.

Используя приведенное выше уравнение, вероятность того, что ровно два броска из четырех общих бросков приведут к выпадению орла, определяется следующим образом:

${\displaystyle {\begin{aligned}P(2)&={4 \choose 2}p^{2}q^{4-2}\\&=6\times \left({\tfrac {1}{2}}\right)^{2}\times \left({\tfrac {1}{2}}\right)^{2}\\&={\dfrac {3}{8}}.\end{aligned}}}$

Смотрите также

• Схема Бернулли
• Выборка Бернулли
• Распределение Бернулли
• Биномиальное распределение
• Биномиальный коэффициент
• Биномиальная пропорция, доверительный интервал
• Выборка по Пуассону
• Выборочный дизайн
• Подбрасывание монеты
• Джейкоб Бернулли
• Точный тест Фишера
• тест Бошлоо

Рекомендации

1. Папулис, А. (1984). «Процессы Бернулли». Вероятность, случайные величины и случайные процессы (2-е изд.). Нью-Йорк: МакГроу-Хилл . стр. 57–63.
2. Джеймс Виктор Успенский: Введение в математическую вероятность , МакГроу-Хилл, Нью-Йорк, 1937, стр. 45
3. Раджив Мотвани и П. Рагхаван. Рандомизированные алгоритмы. Издательство Кембриджского университета, Нью-Йорк (Нью-Йорк), 1995, стр.67-68.

Внешние ссылки

• «Испытания Бернулли», Математическая энциклопедия , EMS Press , 2001 [1994]
• «Моделирование испытаний Бернулли». math.uah.edu . Проверено 21 января 2014 г.