Аккорд (одноранговый)

Протокол для распределенной хэш-таблицы

В вычислительной технике Chord — это протокол и алгоритм для одноранговой распределенной хэш-таблицы . Распределенная хэш-таблица хранит пары ключ-значение , назначая ключи разным компьютерам (известным как «узлы»); узел будет хранить значения для всех ключей, за которые он отвечает. Chord определяет, как ключи назначаются узлам, и как узел может обнаружить значение для данного ключа, сначала найдя узел, отвечающий за этот ключ.

Chord — один из четырёх оригинальных протоколов распределённых хэш-таблиц , наряду с CAN , Tapestry и Pastry . Он был представлен в 2001 году Ионом Стоикой , Робертом Моррисом , Дэвидом Каргером , Франсом Каашоком и Хари Балакришнаном и был разработан в Массачусетском технологическом институте . ^[1] Статья Chord 2001 года ^[1] получила награду ACM SIGCOMM Test of Time в 2011 году. ^[2]

Последующие исследования Памелы Заве показали, что исходный алгоритм Chord (как указано в статье SIGCOMM 2001 года ^[1] , Техническом отчете 2001 года ^[3] , статье PODC 2002 года ^[4] и статье TON 2003 года ^[5] ) может неправильно упорядочить кольцо, создать несколько колец и разорвать кольцо. ^[6]

Обзор

Узлам и ключам назначается -битный идентификатор с использованием согласованного хеширования . Алгоритм SHA-1 является базовой функцией хеширования для согласованного хеширования. Согласованное хеширование является неотъемлемой частью надежности и производительности Chord, поскольку и ключи, и узлы (фактически, их IP-адреса ) равномерно распределены в одном и том же пространстве идентификаторов с незначительной вероятностью коллизии . Таким образом, это также позволяет узлам присоединяться к сети и покидать ее без сбоев. В протоколе термин узел используется для обозначения как самого узла, так и его идентификатора (ID) без двусмысленности. То же самое относится и к термину ключ . ${\displaystyle m}$

Используя протокол поиска Chord, узлы и ключи размещаются в круге идентификаторов, который содержит не более узлов в диапазоне от до . ( должен быть достаточно большим, чтобы избежать коллизий.) Некоторые из этих узлов будут сопоставлены с машинами или ключами, в то время как другие (большинство) будут пустыми. ${\displaystyle 2^{m}}$ ${\displaystyle 0}$ ${\displaystyle 2^{m}-1}$ ${\displaystyle m}$

Каждый узел имеет преемника и предшественника . Преемником узла является следующий узел в круге идентификаторов по часовой стрелке. Предшественником является узел против часовой стрелки. Если для каждого возможного идентификатора есть узел, преемником узла 0 является узел 1, а предшественником узла 0 является узел ; однако, как правило, в последовательности есть «дыры». Например, преемником узла 153 может быть узел 167 (а узлы от 154 до 166 не существуют); в этом случае предшественником узла 167 будет узел 153. ${\displaystyle 2^{m}-1}$

Концепция преемника может использоваться и для ключей. Узел-преемник ключа — это первый узел, идентификатор которого равен или следует за ним в круге идентификатора, обозначенном как . Каждый ключ назначается (хранится) своему узлу-преемнику, поэтому поиск ключа заключается в запросе . ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle successor(k)}$ ${\displaystyle k}$ ${\displaystyle successor(k)}$

Поскольку преемник (или предшественник) узла может исчезнуть из сети (из-за сбоя или ухода), каждый узел записывает дугу узлов, в середине которой он находится, т. е. список узлов, предшествующих ему, и узлов, следующих за ним. Этот список приводит к высокой вероятности того, что узел сможет правильно определить местонахождение своего преемника или предшественника, даже если рассматриваемая сеть страдает от высокой частоты отказов. ${\displaystyle 2r+1}$ ${\displaystyle r}$ ${\displaystyle r}$

Подробности протокола

Сеть Хорда из 16 узлов. Выделены «пальцы» одного из узлов.

Базовый запрос

Основное использование протокола Chord — запрос ключа у клиента (обычно также узла), т. е. поиск . Основной подход — передача запроса преемнику узла, если он не может найти ключ локально. Это приведет к времени запроса, где — количество машин в кольце. ${\displaystyle successor(k)}$ ${\displaystyle O(N)}$ ${\displaystyle N}$

Таблица пальцев

Чтобы избежать линейного поиска выше, Chord реализует более быстрый метод поиска, требуя от каждого узла хранить таблицу finger, содержащую до записей, напомним, что это число бит в хэш-ключе. Запись узла будет содержать . Первая запись таблицы finger на самом деле является непосредственным преемником узла (и поэтому дополнительное поле преемника не требуется). Каждый раз, когда узел хочет найти ключ , он будет передавать запрос ближайшему преемнику или предшественнику (в зависимости от таблицы finger) в своей таблице finger («самому большому» на круге, идентификатор которого меньше ), пока узел не обнаружит, что ключ хранится в его непосредственном преемнике. ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle i^{th}}$ ${\displaystyle n}$ ${\displaystyle successor((n+2^{i-1})\,{\bmod {\,}}2^{m})}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k}$

При использовании такой таблицы пальцев количество узлов, с которыми необходимо связаться, чтобы найти преемника в сети из N узлов, равно . (См. доказательство ниже.) ${\displaystyle O(\log N)}$

Соединение узлов

При каждом присоединении нового узла необходимо поддерживать три инварианта (первые два обеспечивают корректность, а последний поддерживает быструю обработку запросов):

1. Последующий элемент каждого узла правильно указывает на своего непосредственного преемника.
2. Каждый ключ хранится в . ${\displaystyle successor(k)}$
3. Таблица пальцев каждого узла должна быть правильной.

Для удовлетворения этих инвариантов поле предшественника поддерживается для каждого узла. Поскольку преемник является первой записью таблицы finger, нам больше не нужно поддерживать это поле отдельно. Для вновь присоединенного узла должны быть выполнены следующие задачи : ${\displaystyle n}$

1. Инициализируем узел (предшественник и таблицу пальцев). ${\displaystyle n}$
2. Уведомить другие узлы о необходимости обновления их предшественников и таблиц Finger.
3. Новый узел принимает ответственные ключи от своего преемника.

Предшественник может быть легко получен из предшественника (в предыдущем круге). Что касается его таблицы finger, существуют различные методы инициализации. Самый простой из них — выполнить запросы find successor для всех записей, что приводит к времени инициализации. Лучший метод — проверить, является ли запись в таблице finger все еще корректной для записи. Это приведет к . Лучший метод — инициализировать таблицу finger из ее непосредственных соседей и внести некоторые обновления, что является . ${\displaystyle n}$ ${\displaystyle successor(n)}$ ${\displaystyle m}$ ${\displaystyle O(M\log N)}$ ${\displaystyle i^{th}}$ ${\displaystyle (i+1)^{th}}$ ${\displaystyle O(\log ^{2}N)}$ ${\displaystyle O(\log N)}$

Стабилизация

Для обеспечения корректного поиска все указатели-преемники должны быть актуальными. Поэтому в фоновом режиме периодически запускается протокол стабилизации, который обновляет таблицы пальцев и указатели-преемники.

Протокол стабилизации работает следующим образом:

• Stabilize(): n запрашивает у своего преемника предшествующего элемента p и решает, должен ли p быть преемником n (это происходит, если p недавно присоединился к системе).
• Notify(): уведомляет преемника n о его существовании, чтобы он мог изменить своего предшественника на n
• Fix_fingers(): обновляет таблицы пальцев

Потенциальные возможности использования

• Кооперативное зеркалирование: механизм балансировки нагрузки локальной сетью, размещающей информацию, доступную компьютерам за пределами локальной сети. Эта схема может позволить разработчикам балансировать нагрузку между многими компьютерами вместо центрального сервера, чтобы гарантировать доступность своего продукта.
• Хранилище с разделением времени: В сети, как только компьютер подключается к сети, его доступные данные распределяются по всей сети для извлечения, когда этот компьютер отключается от сети. Также данные других компьютеров отправляются на рассматриваемый компьютер для офлайн-извлечения, когда они больше не подключены к сети. В основном для узлов без возможности постоянного подключения к сети.
• Распределенные индексы: Извлечение файлов по сети в доступной для поиска базе данных. Например, клиенты передачи файлов P2P.
• Крупномасштабные комбинаторные поиски: ключи являются потенциальными решениями проблемы, и каждый ключ сопоставляется с узлом или компьютером, который отвечает за оценку их как решения или нет. Например, взлом кода
• Также используется в беспроводных сенсорных сетях для обеспечения надежности ^[7]

Эскизы для проверки

Маршрутный путь между узлами A и B. Каждый переход сокращает оставшееся расстояние вдвое (или лучше).

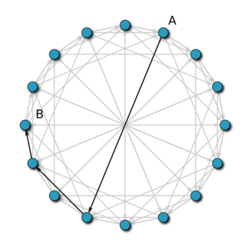
С высокой вероятностью Chord связывается с узлами, чтобы найти преемника в сети из -узлов. ${\displaystyle O(\log N)}$ ${\displaystyle N}$

Предположим, что узел хочет найти преемника ключа . Пусть будет предшественником . Мы хотим найти верхнюю границу для количества шагов, необходимых для маршрутизации сообщения от до . Узел проверит свою таблицу finger и направит запрос ближайшему предшественнику , который у него есть. Назовем этот узел . Если — запись в таблице finger , то оба и находятся на расстоянии между и от вдоль круга идентификатора. Следовательно, расстояние между и вдоль этого круга не превышает . Таким образом, расстояние от до меньше расстояния от до : новое расстояние до не превышает половины исходного расстояния. ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle p}$ ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle p}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle i^{th}}$ ${\displaystyle n}$ ${\displaystyle f}$ ${\displaystyle p}$ ${\displaystyle 2^{i-1}}$ ${\displaystyle 2^{i}}$ ${\displaystyle n}$ ${\displaystyle f}$ ${\displaystyle p}$ ${\displaystyle 2^{i-1}}$ ${\displaystyle f}$ ${\displaystyle p}$ ${\displaystyle n}$ ${\displaystyle f}$ ${\displaystyle p}$

Этот процесс деления оставшегося расстояния пополам повторяется, поэтому после шагов оставшееся расстояние составляет не более ; в частности, после шагов оставшееся расстояние составляет не более . Поскольку узлы распределены равномерно и случайным образом по окружности идентификатора, ожидаемое количество узлов, попадающих в интервал этой длины, равно 1, и с высокой вероятностью таких узлов меньше . Поскольку сообщение всегда продвигается по крайней мере на один узел, для прохождения этого оставшегося расстояния сообщению требуется не более шагов. Таким образом, общее ожидаемое время маршрутизации составляет . ${\displaystyle t}$ ${\displaystyle p}$ ${\displaystyle 2^{m}/2^{t}}$ ${\displaystyle \log N}$ ${\displaystyle 2^{m}/N}$ ${\displaystyle \log N}$ ${\displaystyle \log N}$ ${\displaystyle O(\log N)}$

Если Chord отслеживает предшественников/последователей, то с высокой вероятностью, если каждый узел имеет вероятность отказа 1/4, find_successor (см. ниже) и find_predecessor (см. ниже) вернут правильные узлы. ${\displaystyle r=O(\log N)}$

Проще говоря, вероятность того, что все узлы выйдут из строя , равна , что является низкой вероятностью; поэтому с высокой вероятностью по крайней мере один из них будет активен, и узел будет иметь правильный указатель. ${\displaystyle r}$ ${\displaystyle \left({{1} \over {4}}\right)^{r}=O\left({{1} \over {N}}\right)}$

Псевдокод

Определения псевдокода

палец[к]

первый узел, который успешно ${\displaystyle (n+2^{k-1}){\mbox{ mod }}2^{m},1\leq k\leq m}$

преемник

следующий узел от рассматриваемого узла на кольце идентификаторов

предшественник

предыдущий узел от рассматриваемого узла на кольце идентификаторов

Ниже приведен псевдокод для поиска последующего узла идентификатора:

// запросить у узла n найти преемника id n.find_successor(id)  // Да, это должна быть закрывающая квадратная скобка, соответствующая открывающей круглой скобке.  // Это полузакрытый интервал.  если id ∈ (n, successor] , то  вернуть преемника, иначе // переслать запрос по кругу n0 := ближайший_предшествующий_узел(id) вернуть n0.find_successor(id)// поиск в локальной таблице наивысшего предшественника id n.closest_preceding_node(id)  for i = m downto 1 do  if (finger[i] ∈ (n, id)) then вернуть палец[i] вернуть н

Псевдокод для стабилизации хордового кольца/окружности после соединения и разъединения узлов выглядит следующим образом:

// создаем новое кольцо аккордов. n.create() предшественник := ноль преемник := n// присоединяем кольцо Chord, содержащее узел n'. n.join(n') предшественник := ноль преемник := n'.find_successor(n)// вызывается периодически. n спрашивает преемника // о его предшественнике, проверяет, является ли непосредственный // преемник n согласованным, и сообщает преемнику о n n.stabilize() x = преемник.предшественник если x ∈ (n, преемник), то преемник := x преемник.уведомить(n)// n' думает, что это может быть наш предшественник. n.notify(n')  если предшественник равен nil или n'∈(predecessor, n) тогда предшественник := n'// вызывается периодически. обновляет записи таблицы пальцев. // затем сохраняет индекс пальца для исправления n.fix_fingers() следующий := следующий + 1 если следующий > м тогда следующий := 1 палец[следующий] := find_successor(n+2 следующий-1 );// вызывается периодически. проверяет, не произошел ли сбой предшественника. n.check_predecessor()  если предшественник произошел сбой , то предшественник := ноль

Смотрите также

• Кадемлия
• Коорде
• OverSim – фреймворк наложенного моделирования
• SimGrid – набор инструментов для моделирования распределенных приложений -

Ссылки

1. Stoica, I. ; Morris, R.; Kaashoek, MF; Balakrishnan, H. (2001). "Chord: масштабируемая одноранговая служба поиска для интернет-приложений" (PDF) . ACM SIGCOMM Computer Communication Review . 31 (4): 149. doi :10.1145/964723.383071.
2. "ACM SIGCOMM Test of Time Paper Award" . Получено 16 января 2022 г. .
3. Stoica, I. ; Morris, R.; Liben-Nowell, D.; Karger, D.; Kaashoek, MF; Dabek, F.; Balakrishnan, H. (2001). Chord: масштабируемая одноранговая служба поиска для интернет-приложений (PDF) (технический отчет). MIT LCS. MIT. 819. Архивировано из оригинала (PDF) 22 июля 2012 г.
4. Либен-Ноуэлл, Дэвид; Балакришнан, Хари; Каргер, Дэвид (июль 2002 г.). Анализ эволюции одноранговых систем (PDF) . PODC '02: Труды двадцать первого ежегодного симпозиума по принципам распределенных вычислений. стр. 233–242. doi :10.1145/571825.571863.
5. Stoica, I. ; Morris, R.; Liben-Nowell, D.; Karger, D.; Kaashoek, MF; Dabek, F.; Balakrishnan, H. (25 февраля 2003 г.). «Chord: масштабируемый протокол однорангового поиска для интернет-приложений». IEEE/ACM Transactions on Networking . 11 (1): 17–32. doi :10.1109/TNET.2002.808407. S2CID  221276912.
6. Zave, Pamela (2012). «Использование облегченного моделирования для понимания аккорда» (PDF) . ACM SIGCOMM Computer Communication Review . 42 (2): 49–57. doi :10.1145/2185376.2185383. S2CID  11727788.
7. Лаббай, Пир Мира (осень 2016 г.). "T2WSN: ИЗОБРЕТЕННОЕ ДВУХШИННОЕ НАЛОЖЕНИЕ АККОРДА, ПОМОГАЮЩЕЕ ПОВЫШЕНИЮ НАДЕЖНОСТИ И КОЭФФИЦИЕНТА ДОСТАВКИ ДЛЯ БЕСПРОВОДНЫХ СЕНСОРНЫХ СЕТЕЙ" (PDF) . Журнал теоретических и прикладных информационных технологий . 91 : 168–176.

Внешние ссылки

• Проект «Аккорд» (перенаправление с: http://pdos.lcs.mit.edu/chord/)
• Open Chord – реализация Java с открытым исходным кодом
• Chordless – еще одна реализация Java с открытым исходным кодом
• jDHTUQ — реализация Java с открытым исходным кодом. API для обобщения реализации одноранговых систем DHT. Содержит GUI в структуре данных режима