Энергетический профиль (химия)

Представление химического процесса как единого энергетического пути

В теоретической химии энергетический профиль — это теоретическое представление химической реакции или процесса в виде единого энергетического пути, по которому реагенты превращаются в продукты . Этот путь проходит вдоль координаты реакции , которая представляет собой параметрическую кривую , которая следует за путем реакции и указывает на ее ход; таким образом, энергетические профили также называются диаграммами координат реакции . Они выводятся из соответствующей поверхности потенциальной энергии (ППЭ), которая используется в вычислительной химии для моделирования химических реакций путем связывания энергии молекулы(молекул) с ее структурой (в рамках приближения Борна–Оппенгеймера ).

Рисунок 1: Координатная диаграмма реакции: исходное вещество или реагент A преобразуется в продукт C через переходное состояние B с помощью энергии активации ΔG ^≠ , после чего высвобождается химическая энергия ΔG°

Качественно, диаграммы координат реакции (одномерные энергетические поверхности) имеют многочисленные приложения. Химики используют диаграммы координат реакции как аналитическое и педагогическое пособие для рационализации и иллюстрации кинетических и термодинамических событий. Целью энергетических профилей и поверхностей является предоставление качественного представления того, как потенциальная энергия изменяется с молекулярным движением для данной реакции или процесса. ^[1]

Поверхности потенциальной энергии

Проще говоря, поверхность потенциальной энергии или ППЭ — это математическое или графическое представление связи между энергией молекулы и ее геометрией. Методы описания потенциальной энергии делятся на интерпретацию классической механики ( молекулярную механику ) и интерпретацию квантовой механики . В квантово-механической интерпретации точное выражение для энергии может быть получено для любой молекулы, выведенной из квантовых принципов (хотя может потребоваться бесконечный базисный набор), но расчеты/методы ab initio часто будут использовать приближения для снижения вычислительных затрат. ^{[2] [3]} Молекулярная механика основана на эмпирических данных, а потенциальная энергия описывается как функция компонентных членов, которые соответствуют отдельным потенциальным функциям, таким как кручение , растяжения, изгибы, энергии Ван-дер-Ваальса , электростатика и перекрестные члены. ^{[3] [4] [5]} Каждая компонентная потенциальная функция соответствует экспериментальным данным или свойствам, предсказанным расчетами ab initio . ^[4] Молекулярная механика полезна для прогнозирования равновесных геометрий и переходных состояний , а также относительной конформационной стабильности. В процессе реакции атомы участвующих молекул обычно претерпевают некоторые изменения в пространственной ориентации посредством внутреннего движения, а также электронного окружения. ^[1] Искажения геометрических параметров приводят к отклонению от равновесной геометрии (локальные минимумы энергии). Эти изменения геометрии молекулы или взаимодействия между молекулами являются динамическими процессами, которые требуют понимания всех сил, действующих внутри системы. Поскольку эти силы могут быть математически выведены как первая производная потенциальной энергии по смещению, имеет смысл отобразить потенциальную энергию E системы как функцию геометрических параметров q ₁ , q ₂ , q ₃ и так далее. ^[1] Потенциальная энергия при заданных значениях геометрических параметров ( q ₁ , q ₂ , ..., q _n ) представлена ​​в виде гиперповерхности (когда n > 2 ) или поверхности (когда n ≤ 2 ). Математически это можно записать как

${\displaystyle E=f(q_{1},q_{2},\dots ,q_{n})}$

Для квантово-механической интерпретации ППЭ обычно определяется в приближении Борна-Оппенгеймера (чтобы различать ядерное и электронное движение и энергию), которое утверждает, что ядра неподвижны относительно электронов. Другими словами, приближение позволяет пренебречь кинетической энергией ядер (или движением ядер), и поэтому отталкивание ядер является постоянной величиной (как статические точечные заряды ) и учитывается только при расчете полной энергии системы. Затем принимается, что электронная энергия параметрически зависит от ядерных координат, что означает, что для каждой соответствующей атомной конфигурации должна быть рассчитана новая электронная энергия ( E _e ^{). [2] [3]}

ПЭС является важной концепцией в вычислительной химии и существенно помогает в оптимизации геометрии и переходного состояния.

Степени свободы

Система из n атомов определяется 3 n координатами: ( x , y , z ) для каждого атома. Эти 3 n степеней свободы можно разбить на 3 общие поступательные и 3 (или 2) общие вращательные степени свободы для нелинейной системы (для линейной системы). Однако общие поступательные или вращательные степени не влияют на потенциальную энергию системы, которая зависит только от ее внутренних координат. Таким образом, система из n атомов будет определяться 3 n – 6 (нелинейными) или 3 n – 5 (линейными) координатами. ^{[1] [3]} Эти внутренние координаты могут быть представлены простыми координатами растяжения, изгиба, кручения или линейными комбинациями, адаптированными к симметрии, или избыточными координатами, или координатами нормальных мод и т. д. Для системы, описываемой n- внутренними координатами, можно записать отдельную функцию потенциальной энергии относительно каждой из этих координат, удерживая другие n – 1 параметры на постоянном значении, что позволяет контролировать вклад потенциальной энергии от конкретного молекулярного движения (или взаимодействия), пока определяются другие n – 1 параметры.

Рассмотрим двухатомную молекулу AB, которую можно макроскопически визуализировать как два шара (которые изображают два атома A и B), соединенных пружиной, которая изображает связь. Когда эта пружина (или связь) растягивается или сжимается, потенциальная энергия системы шар-пружина (молекула AB) изменяется, и это можно отобразить на двумерном графике как функцию расстояния между A и B, т. е. длины связи.

Рисунок 2: Модель шара и пружины для двухатомной молекулы — атомы A и B соединены связью (пружиной). Потенциальная энергия — это функция расстояния r от точки равновесия.

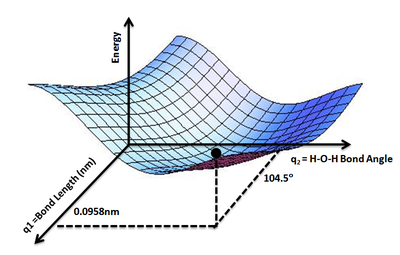
Эту концепцию можно расширить до трехатомной молекулы, такой как вода, где у нас есть две связи O−H и угол связи H−O−H в качестве переменных, от которых будет зависеть потенциальная энергия молекулы воды. Мы можем с уверенностью предположить, что две связи O−H равны. Таким образом, можно нарисовать ППЭ, отображающую потенциальную энергию E молекулы воды как функцию двух геометрических параметров, q ₁ = длина связи O–H и q ₂ = угол связи H–O–H . Самая низкая точка на такой ППЭ будет определять равновесную структуру молекулы воды.

Рисунок 3: ППЭ для молекулы воды:
показывает минимум энергии, соответствующий оптимизированной молекулярной структуре для воды, длина связи O−H 0,0958 нм и угол связи H−O−H 104,5°

Та же концепция применяется к органическим соединениям, таким как этан , бутан и т. д., чтобы определить их наиболее низкоэнергетические и стабильные конформации .

Характеристика ПЭС

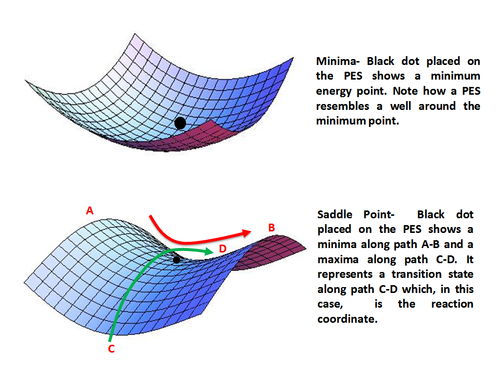
Наиболее важными точками на ППЭ являются стационарные точки , где поверхность плоская, т. е. параллельная горизонтальной линии, соответствующей одному геометрическому параметру, плоскости, соответствующей двум таким параметрам, или даже гиперплоскости, соответствующей более чем двум геометрическим параметрам. Значения энергии, соответствующие переходным состояниям и основному состоянию реагентов и продуктов, можно найти с помощью функции потенциальной энергии, вычислив критические точки функции или стационарные точки. Стационарные точки возникают, когда первая частная производная энергии по каждому геометрическому параметру равна нулю.

${\displaystyle {\frac {\partial E}{\partial q_{1}}}={\frac {\partial E}{\partial q_{2}}}=\dots ={\frac {\partial E}{\partial q_{n}}}=0}$

Используя аналитические производные полученного выражения для энергии, можно найти и охарактеризовать стационарную точку как минимум, максимум или седловую точку . Основные состояния представлены локальными минимумами энергии, а переходные состояния — седловыми точками. ${\displaystyle E=f(q_{1},q_{2},\dots ,q_{n}),}$

Минимумы представляют стабильные или квазистабильные виды, т.е. реагенты и продукты с конечным временем жизни. Математически точка минимума задается как

${\displaystyle {\frac {\partial E}{\partial q_{1}}}=0}$

${\displaystyle {\frac {\partial ^{2}E}{\partial q_{1}^{2}}}>0}$

Точка может быть локальным минимумом, если ее энергия ниже по сравнению только с окружающей средой, или глобальным минимумом, если это точка с самой низкой энергией на всей поверхности потенциальной энергии.

Седловая точка представляет максимум только по одному направлению (координате реакции) и является минимумом по всем остальным направлениям. Другими словами, седловая точка представляет переходное состояние по координате реакции. Математически седловая точка возникает, когда

${\displaystyle {\frac {\partial ^{2}E}{\partial q^{2}}}>0}$

для всех q, за исключением координаты реакции и

${\displaystyle {\frac {\partial ^{2}E}{\partial q_{1}^{2}}}<0}$

вдоль координаты реакции.

Рисунок 4:
Минимумы (вверху) и седловая точка (внизу) на поверхности потенциальной энергии

Диаграммы координат реакции

Внутренняя координата реакции ^[6] (IRC), полученная из поверхности потенциальной энергии, представляет собой параметрическую кривую, которая соединяет два минимума энергии в направлении, которое пересекает минимальный энергетический барьер (или самый пологий подъем), проходя через одну или несколько седловых точек. Однако в действительности, если реагирующие частицы достигают достаточной энергии, они могут в некоторой степени отклониться от IRC. ^[1] Значения энергии (точки на гиперповерхности) вдоль координаты реакции приводят к одномерной энергетической поверхности (линии), а при построении относительно координаты реакции (энергия против координаты реакции) дают то, что называется диаграммой координат реакции (или энергетическим профилем). Другой способ визуализации энергетического профиля — это поперечное сечение гиперповерхности или поверхности вдоль координаты реакции. На рисунке 5 показан пример поперечного сечения, представленного плоскостью, взятой вдоль координаты реакции, а потенциальная энергия представлена ​​как функция или составная часть двух геометрических переменных для формирования двухмерной энергетической поверхности. В принципе, функция потенциальной энергии может зависеть от N переменных, но поскольку точное визуальное представление функции 3 или более переменных не может быть получено (исключая гиперповерхности уровня ), была показана 2-мерная поверхность. Точки на поверхности, которые пересекают плоскость, затем проецируются на диаграмму координат реакции (показанную справа) для получения 1-мерного среза поверхности вдоль IRC. Координата реакции описывается ее параметрами, которые часто задаются как составная часть нескольких геометрических параметров, и может менять направление по мере протекания реакции, пока преодолевается наименьший энергетический барьер (или энергия активации (Ea)). ^[1] Седловая точка представляет собой самую высокую энергетическую точку, лежащую на координате реакции, соединяющей реагент и продукт; это известно как переходное состояние. Диаграмма координат реакции может также иметь один или несколько переходных промежуточных продуктов, которые показаны высокоэнергетическими ямами, соединенными через пик переходного состояния. Любая химическая структура, которая сохраняется дольше времени типичных колебаний связей (10−13 ^– 10−14 ^с ), может рассматриваться как промежуточная. ^[4]

Рисунок 5: Поверхность потенциальной энергии и соответствующая двумерная диаграмма координат реакции, полученная из плоскости, проходящей через путь минимальной энергии между A и C и проходящей через B.

Реакция, включающая более одного элементарного шага, имеет один или несколько промежуточных продуктов, которые, в свою очередь, означают, что необходимо преодолеть более одного энергетического барьера. Другими словами, на пути реакции лежит более одного переходного состояния. Поскольку интуитивно понятно, что преодоление энергетического барьера или прохождение через пик переходного состояния повлечет за собой самую высокую энергию, становится ясно, что это будет самый медленный шаг в пути реакции. Однако, когда необходимо преодолеть более одного такого барьера, становится важным распознать самый высокий барьер, который определит скорость реакции. Этот шаг реакции, скорость которого определяет общую скорость реакции, известен как шаг, определяющий скорость, или шаг, ограничивающий скорость. Высота энергетического барьера всегда измеряется относительно энергии реагента или исходного материала. Различные возможности показаны на рисунке 6.

Рисунок 6: Диаграммы координат реакции, показывающие реакции с 0, 1 и 2 промежуточными продуктами: Двунаправленная стрелка показывает первый, второй и третий шаг на каждой диаграмме координат реакции. Во всех трех этих реакциях первый шаг является медленным, поскольку энергия активации от реагентов до переходного состояния самая высокая. На последующих шагах энергия активации только от промежуточного до следующего переходного состояния. ^[4]

Координатные диаграммы реакции также дают информацию о равновесии между реагентом или продуктом и промежуточным продуктом. Если барьерная энергия для перехода от промежуточного продукта к продукту намного выше, чем для перехода от реагента к промежуточному продукту, можно с уверенностью заключить, что между реагентом и промежуточным продуктом установлено полное равновесие. Однако, если два энергетических барьера для превращения реагента в промежуточный продукт и промежуточного продукта почти равны, то полное равновесие не устанавливается, и для вывода выражений кинетической скорости для такой реакции используется приближение стационарного состояния. ^[7]

Рисунок 7: Координатные диаграммы реакции: реакция с равновесием между реагентом и промежуточным продуктом (слева) и реакция без такого равновесия (справа) ^[4]

Построение диаграммы координат реакции

Хотя диаграмма координат реакции по сути выводится из поверхности потенциальной энергии, не всегда возможно нарисовать ее из ППЭ. Химик рисует диаграмму координат реакции для реакции, основываясь на знании свободной энергии или изменения энтальпии, связанного с преобразованием, что помогает ему поместить реагент и продукт в перспективу и определить, образуется ли какой-либо промежуточный продукт или нет. Одним из руководящих принципов для рисования диаграмм для сложных реакций является принцип наименьшего движения , который гласит, что предпочтительная реакция, идущая от реагента к промежуточному продукту или от одного промежуточного продукта к другому или продукту, — это та, которая имеет наименьшее изменение в ядерном положении или электронной конфигурации. Таким образом, можно сказать, что реакции, включающие резкие изменения в положении ядер, на самом деле происходят через серию простых химических реакций. Постулат Хаммонда — еще один инструмент, который помогает извлечь энергию переходного состояния относительно реагента, промежуточного продукта или продукта. Он гласит, что переходное состояние напоминает реагент, промежуточный продукт или продукт, к которому оно ближе всего по энергии, пока разница в энергии между переходным состоянием и смежной структурой не слишком велика. Этот постулат помогает точно предсказать форму координатной диаграммы реакции, а также дает представление о молекулярной структуре в переходном состоянии.

Кинетические и термодинамические соображения

Химическая реакция может быть определена двумя важными параметрами — свободной энергией Гиббса , связанной с химическим превращением, и скоростью такого превращения. Эти параметры независимы друг от друга. В то время как изменение свободной энергии описывает стабильность продуктов относительно реагентов, скорость любой реакции определяется энергией переходного состояния относительно исходного материала. В зависимости от этих параметров реакция может быть благоприятной или неблагоприятной, быстрой или медленной, обратимой или необратимой, как показано на рисунке 8.

Благоприятная реакция — это та, в которой изменение свободной энергии ∆ G ° отрицательно ( экзергоническая ) или, другими словами, свободная энергия продукта, G ° _product , меньше свободной энергии исходных материалов, G ° _reactant . ∆ G °> 0 ( эндергоническая ) соответствует неблагоприятной реакции. ∆ G ° можно записать как функцию изменения энтальпии ( ∆ H °) и изменения энтропии (∆ S °) как ∆ G °= ∆ H ° – T ∆ S ° . На практике для определения того, является ли реакция благоприятной или неблагоприятной, используются энтальпии, а не свободная энергия, поскольку ∆ H ° легче измерить, а T ∆ S ° обычно слишком мала, чтобы иметь какое-либо значение (для T < 100 °C). Реакция с ∆ H °<0 называется экзотермической , а с ∆ H °>0 — эндотермической .

Рисунок 8: Диаграммы координат реакции, показывающие благоприятные или неблагоприятные, а также медленные или быстрые реакции ^[7]

Относительная стабильность реагента и продукта сама по себе не определяет осуществимость любой реакции. Для того чтобы любая реакция могла протекать, исходный материал должен иметь достаточно энергии, чтобы преодолеть энергетический барьер. Этот энергетический барьер известен как энергия активации (∆ G ^≠ ), и скорость реакции зависит от высоты этого барьера. Низкий энергетический барьер соответствует быстрой реакции, а высокий энергетический барьер соответствует медленной реакции. Реакция находится в равновесии, когда скорость прямой реакции равна скорости обратной реакции. Такая реакция называется обратимой. Если исходный материал и продукт(ы) находятся в равновесии, то их относительное содержание определяется разницей в свободной энергии между ними. В принципе, все элементарные стадии обратимы, но во многих случаях равновесие лежит так далеко в сторону продукта, что исходный материал фактически больше не наблюдается или присутствует в достаточной концентрации, чтобы влиять на реакционную способность. Практически говоря, реакция считается необратимой.

Хотя большинство обратимых процессов будут иметь достаточно малый K , равный 10 ³ или меньше, это не является жестким правилом, и ряд химических процессов требуют обратимости даже очень благоприятных реакций. Например, реакция карбоновой кислоты с аминами с образованием соли происходит при K, равном 10 ^5–6 , и при обычных температурах этот процесс считается необратимым. Тем не менее, при достаточном нагревании происходит обратная реакция, что позволяет образовать тетраэдрический промежуточный продукт и, в конечном итоге, амид и воду. (Для экстремального примера, требующего обратимости шага с K > 10 ¹¹ , см. деметилирование .) Реакция также может стать необратимой, если происходит последующий, более быстрый шаг для потребления исходного продукта(ов) или в открытой системе выделяется газ. Таким образом, не существует значения K , которое служило бы «разделительной линией» между обратимыми и необратимыми процессами. Вместо этого обратимость зависит от временных рамок, температуры, условий реакции и общего энергетического ландшафта.

Когда реагент может образовывать два разных продукта в зависимости от условий реакции, становится важным выбрать правильные условия, благоприятствующие желаемому продукту. Если реакция проводится при относительно более низкой температуре, то образующийся продукт лежит по ту сторону меньшего энергетического барьера. Это называется кинетическим контролем, и соотношение образующихся продуктов зависит от относительных энергетических барьеров, ведущих к продуктам. Относительная стабильность продуктов не имеет значения. Однако при более высоких температурах молекулы имеют достаточно энергии, чтобы пересечь оба энергетических барьера, ведущих к продуктам. В таком случае соотношение продуктов определяется исключительно энергиями продуктов, а энергии барьера не имеют значения. Это известно как термодинамический контроль, и его можно достичь только тогда, когда продукты могут взаимно преобразовываться и уравновешиваться в условиях реакции. Диаграмма координат реакции также может быть использована для качественной иллюстрации кинетического и термодинамического контроля в реакции.

Рисунок 9: Кинетический и термодинамический контроль: A. Продукт B является как кинетическим, так и термодинамическим продуктом, а B. Продукт A является кинетическим продуктом, а B — термодинамическим продуктом. ^[4]

Приложения

Ниже приведены несколько примеров того, как интерпретировать диаграммы координат реакций и использовать их при анализе реакций.

Эффект растворителя: В общем, если переходное состояние для этапа определения скорости соответствует более заряженным видам относительно исходного материала, то увеличение полярности растворителя увеличит скорость реакции, поскольку более полярный растворитель будет более эффективен в стабилизации переходного состояния (ΔG ^‡ уменьшится). Если структура переходного состояния соответствует менее заряженным видам, то увеличение полярности растворителя уменьшит скорость реакции, поскольку более полярный растворитель будет более эффективен в стабилизации исходного материала (ΔG ^o уменьшится, что, в свою очередь, увеличит ΔG ^‡ ). ^[8]

С _Н 1 против С _Н 2

Механизмы S _N 1 и S _N 2 используются в качестве примера для демонстрации того, как эффекты растворителя могут быть отображены на диаграммах координат реакции.

• S _N 1: На рисунке 10 показан этап определения скорости для механизма S _N 1, образование промежуточного карбокатиона и соответствующая диаграмма координат реакции. Для механизма S _N 1 структура переходного состояния показывает частичную плотность заряда относительно нейтральной структуры основного состояния. Поэтому увеличение полярности растворителя, например, от гексанов (показано синим цветом) до эфира (показано красным цветом), приведет к снижению скорости реакции. Как показано на рисунке 9, исходный материал имеет приблизительно одинаковую стабильность в обоих растворителях (поэтому ΔΔG ^o =ΔG ^o _{полярный} – ΔG ^o _{неполярный} мало), а переходное состояние стабилизировано больше в эфире, что означает ΔΔG ^≠ = ΔG ^≠ _{полярный} – ΔG ^≠ _{неполярный} велико.

Рисунок 10: Показывает энергетический профиль для RDS в механизме S _N 1, когда растворитель меняется с более полярного растворителя (показан красным) на менее полярный растворитель (показан синим). Обратите внимание, что показанная структура переходного состояния имеет частичный заряд.

• S _N 2: Для механизма S _N 2 благоприятен сильноосновный нуклеофил (т. е. заряженный нуклеофил). На рисунке 11 ниже показан этап определения скорости для синтеза эфира Уильямсона . ^{[9] [10]} Исходным материалом является метилхлорид и этоксид-ион, который имеет локализованный отрицательный заряд, что означает, что он более стабилен в полярных растворителях. На рисунке показана структура переходного состояния, когда метилхлорид подвергается нуклеофильной атаке. В структуре переходного состояния заряд распределен между атомами Cl и O, и более полярный растворитель менее эффективен в стабилизации структуры переходного состояния по сравнению с исходными материалами. Другими словами, разница в энергии между полярным и неполярным растворителем больше для основного состояния (для исходного материала), чем в переходном состоянии.

Рисунок 11: Показывает влияние полярности растворителя на механизм S _N 2. Полярный растворитель показан красным, а неполярный растворитель показан синим.

Катализаторы: существует два типа катализаторов , положительные и отрицательные. Положительные катализаторы увеличивают скорость реакции, а отрицательные катализаторы (или ингибиторы) замедляют реакцию и, возможно, приводят к тому, что реакция вообще не происходит. Цель катализатора — изменить энергию активации. Рисунок 12 иллюстрирует цель катализатора, заключающуюся в том, что изменяется только энергия активации , а не относительная термодинамическая стабильность, показанная на рисунке как ΔH, продуктов и реагентов. Это означает, что катализатор не изменит равновесные концентрации продуктов и реагентов, а только позволит реакции достичь равновесия быстрее. Рисунок 13 показывает катализируемый путь, происходящий в несколько этапов, что является более реалистичным изображением катализируемого процесса. Новый катализируемый путь может происходить через тот же механизм, что и некатализируемая реакция, или через альтернативный механизм. ^[4] Фермент — это биологический катализатор, который увеличивает скорость многих жизненно важных биохимических реакций. Рисунок 13 показывает распространенный способ иллюстрации влияния фермента на данную биохимическую реакцию. ^[11]

Рисунок 12: Энергетический профиль, показывающий продукты (Y), реагенты (X), энергию активации (E _a ​​) для эндотермической и экзотермической реакции и энтальпию (ΔH). Также показан профиль для той же реакции, но с катализатором.

Рисунок 13: Диаграмма энергетического профиля, демонстрирующая влияние катализатора на общую экзотермическую реакцию X + Y → Z. Катализатор предлагает альтернативный путь реакции (показан красным), где этап определения скорости имеет меньшую ΔG≠. Относительная термодинамическая стабильность остается прежней.

Смотрите также

• Свободная энергия Гиббса
• Энтальпия
• Энтропия
• Вычислительная химия
• Молекулярная механика
• Приближение Борна-Оппенгеймера

Ссылки

1. Lewars, EG (2011). Вычислительная химия. Springer. стр. 9–43. ISBN 978-9048138616.
2. Сабо, Аттила; Остлунд, Нил (1989). Современная квантовая химия: Введение в передовую теорию электронной структуры . Довер. ISBN 0-486-69186-1.
3. Шеррилл, Дэвид. "Поверхности потенциальной энергии" (PDF) . Получено 27.10.2013 .
4. Anslyn, Dougherty, Eric, Dennis (2006). Современная физическая органическая химия . Книги по университетской науке. ISBN 1-891389-31-9.{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
5. Шеррилл, Дэвид. «Введение в молекулярную механику» (PDF) .
6. IUPAC , Compendium of Chemical Terminology , 2nd ed. («Золотая книга») (1997). Онлайн-исправленная версия: (2006–) «Intrinsic responseordinate». doi :10.1351/goldbook.IT07057
7. Гроссман, Роберт (31 июля 2007 г.). Искусство написания разумных механизмов органических реакций, 2-е изд. Springer. ISBN 978-0-387-95468-4.
8. Брюс, Паула (2007). Органическая химия, 5-е изд . Нью-Джерси: Pearson Prentice Hall. ISBN 978-0-13-196316-0.
9. Ньюман, Роберт (2013). Органическая химия. Роберт С. Ньюман, младший. стр. Гл.7, 1–71.
10. Портал органической химии. "Нуклеофильное замещение" . Получено 25.10.2013 .
11. Сильверман, Ричард (2004). Органическая химия разработки и действия лекарств, 2-е изд. Elsevier. стр. 178. ISBN 0-12-643732-7.