F-тест

Проверка статистической гипотезы, в основном с использованием множественных ограничений

PDF-теста f с d1 и d2 = 10, при уровне значимости 0,05. (Красная затененная область указывает на критическую область)

F - тест — это любой статистический тест, используемый для сравнения дисперсий двух выборок или отношения дисперсий между несколькими выборками. Тестовая статистика , случайная величина F, используется для определения того, имеют ли тестируемые данные F -распределение при истинной нулевой гипотезе и истинных обычных предположениях относительно погрешности (ε). ^[1] Чаще всего он используется при сравнении статистических моделей , подогнанных под набор данных , для того, чтобы определить модель, которая лучше всего подходит для популяции , из которой были отобраны данные. Точные « F -тесты» в основном возникают, когда модели подгоняются под данные с использованием наименьших квадратов . Название было придумано Джорджем В. Снедекором в честь Рональда Фишера . Фишер первоначально разработал статистику как отношение дисперсии в 1920-х годах. ^[2]

Распространенные примеры

Распространенными примерами использования F -тестов являются исследования следующих случаев:

• 

  Таблица однофакторного дисперсионного анализа с 3 случайными группами, каждая из которых содержит 30 наблюдений. Значение F вычисляется в предпоследнем столбце.

  Гипотеза о том, что средние значения заданного набора нормально распределенных совокупностей, все имеющие одинаковое стандартное отклонение , равны. Это, возможно, самый известный F -тест, и он играет важную роль в дисперсионном анализе (ANOVA).
  • F-тест дисперсионного анализа (ANOVA) следует трем предположениям
    1. Нормальность (статистика)
    2. Однородность дисперсии
    3. Независимость от ошибок и случайной выборки

• Гипотеза о том, что предложенная регрессионная модель хорошо соответствует данным . См. Несоответствие суммы квадратов .
• Гипотеза о том, что набор данных в регрессионном анализе следует более простой из двух предложенных линейных моделей, вложенных друг в друга.
• Тестирование множественных сравнений проводится с использованием необходимых данных в уже выполненном F-тесте, если F-тест приводит к отклонению нулевой гипотезы и изучаемый фактор оказывает влияние на зависимую переменную. ^[1]
  • « априорные сравнения»/«плановые сравнения» — определенный набор сравнений
  • «парные сравнения» — все возможные сравнения
    • т.е. тест Фишера на наименьшую значимую разницу (LSD), тест Тьюки на достоверно значимую разницу (HSD) , тест Ньюмена-Кейлса , тест Дюкана
  • « апостериорные сравнения » / « сравнения после получения результатов » / « исследовательские сравнения » - выберите сравнения после изучения данных
    • т.е. метод Шеффе

Ф-тест равенства двух дисперсий

F - тест чувствителен к ненормальности . ^{[3] [4]} В дисперсионном анализе (ANOVA) альтернативные тесты включают тест Левена , тест Бартлетта и тест Брауна-Форсайта . Однако, когда любой из этих тестов проводится для проверки базового предположения о гомоскедастичности ( т.е. однородности дисперсии) в качестве предварительного шага к проверке на средние эффекты, наблюдается увеличение экспериментальной частоты ошибок типа I. ^[5]

Формула и расчет

Большинство F -тестов возникают при рассмотрении разложения изменчивости в наборе данных в терминах сумм квадратов . Тестовая статистика в F -тесте представляет собой отношение двух масштабированных сумм квадратов, отражающих различные источники изменчивости. Эти суммы квадратов построены таким образом, что статистика имеет тенденцию быть больше, когда нулевая гипотеза не верна. Для того чтобы статистика следовала F - распределению при нулевой гипотезе, суммы квадратов должны быть статистически независимыми , и каждая должна следовать масштабированному χ²-распределению . Последнее условие гарантируется, если значения данных независимы и нормально распределены с общей дисперсией .

Однофакторный дисперсионный анализ

Формула для однофакторного F - теста ANOVA имеет вид

${\displaystyle F={\frac {\text{explained variance}}{\text{unexplained variance}}},}$

или

${\displaystyle F={\frac {\text{between-group variability}}{\text{within-group variability}}}.}$

«Объясненная дисперсия» или «межгрупповая изменчивость» — это

${\displaystyle \sum _{i=1}^{K}n_{i}({\bar {Y}}_{i\cdot }-{\bar {Y}})^{2}/(K-1)}$

где обозначает выборочное среднее значение в i -й группе, — количество наблюдений в i -й группе, обозначает общее среднее значение данных, а обозначает количество групп. ${\displaystyle {\bar {Y}}_{i\cdot }}$ ${\displaystyle n_{i}}$ ${\displaystyle {\bar {Y}}}$ ${\displaystyle K}$

«Необъяснимая дисперсия» или «внутригрупповая изменчивость» — это

${\displaystyle \sum _{i=1}^{K}\sum _{j=1}^{n_{i}}\left(Y_{ij}-{\bar {Y}}_{i\cdot }\right)^{2}/(N-K),}$

где - j ^-е наблюдение в i ^-й группе , а - общий размер выборки. Эта F -статистика следует F -распределению со степенями свободы и при нулевой гипотезе. Статистика будет большой, если межгрупповая изменчивость велика по сравнению с внутригрупповой изменчивостью, что вряд ли произойдет, если средние значения совокупности всех групп будут иметь одинаковое значение. ${\displaystyle Y_{ij}}$ ${\displaystyle K}$ ${\displaystyle N}$ ${\displaystyle d_{1}=K-1}$ ${\displaystyle d_{2}=N-K}$

Таблица F: Критические значения уровня 5%, содержащие степени свободы как для знаменателя, так и для числителя в диапазоне от 1 до 20

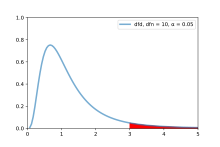
Результат F-теста можно определить, сравнив вычисленное значение F и критическое значение F с определенным уровнем значимости (например, 5%). Таблица F служит справочным руководством, содержащим критические значения F для распределения F-статистики при предположении истинной нулевой гипотезы. Она предназначена для определения порогового значения, за пределами которого ожидается, что F-статистика превысит контролируемый процент времени (например, 5%), когда нулевая гипотеза точна. Чтобы найти критическое значение F в таблице F, необходимо использовать соответствующие степени свободы. Это включает в себя определение соответствующей строки и столбца в таблице F, которые соответствуют проверяемому уровню значимости (например, 5%). ^[6]

Как использовать критические значения F:

Если статистика F < критического значения F

• Не удалось отвергнуть нулевую гипотезу
• Отклонить альтернативную гипотезу
• Нет существенных различий между средними значениями выборки.
• Наблюдаемые различия между средними значениями выборки вполне могли быть вызваны случайностью.
• Результат статистически незначим.

Если статистика F > критического значения F

• Принять альтернативную гипотезу
• Отклонить нулевую гипотезу
• Существуют значительные различия между средними значениями выборки.
• Наблюдаемые различия между средними значениями выборки не могут быть разумно вызваны случайностью.
• Результат статистически значим.

Обратите внимание, что при наличии только двух групп для однофакторного ANOVA F- теста, где t — статистика Стьюдента , ${\displaystyle F=t^{2}}$ ${\displaystyle t}$

Преимущества

• Эффективность сравнения нескольких групп: упрощение одновременного сравнения нескольких групп, повышение эффективности, особенно в ситуациях, в которых участвует более двух групп.
• Ясность в сравнении дисперсий: предоставление простой интерпретации различий дисперсий между группами, способствующее четкому пониманию наблюдаемых закономерностей в данных.
• Универсальность в разных дисциплинах: демонстрация широкой применимости в различных областях, включая социальные науки, естественные науки и инженерию.

Недостатки

• Чувствительность к предположениям: F-тест очень чувствителен к определенным предположениям, таким как однородность дисперсии и нормальность, которые могут повлиять на точность результатов теста.
• Ограниченная область применения для сравнения групп: F-тест предназначен для сравнения дисперсий между группами, что делает его менее подходящим для анализа за пределами этой конкретной области применения.
• Проблемы интерпретации: F-тест не определяет конкретные пары групп с отчетливыми дисперсиями. Необходима тщательная интерпретация, и для более детального понимания различий между группами часто необходимы дополнительные постфактум-тесты.

Проблемы множественного сравнения ANOVA

F -тест в однофакторном дисперсионном анализе ( ANOVA ) используется для оценки того, отличаются ли друг от друга ожидаемые значения количественной переменной в пределах нескольких заранее определенных групп. Например, предположим, что в медицинском исследовании сравниваются четыре метода лечения. F -тест ANOVA можно использовать для оценки того, являются ли какие-либо методы лечения в среднем лучше или хуже других по сравнению с нулевой гипотезой о том, что все четыре метода лечения дают одинаковый средний ответ. Это пример «омнибусного» теста, означающего, что один тест выполняется для обнаружения любого из нескольких возможных различий. В качестве альтернативы мы могли бы провести парные тесты среди методов лечения (например, в примере медицинского исследования с четырьмя методами лечения мы могли бы провести шесть тестов среди пар методов лечения). Преимущество F -теста ANOVA заключается в том, что нам не нужно заранее указывать, какие методы лечения следует сравнивать, и нам не нужно корректировать для проведения множественных сравнений . Недостатком F -теста ANOVA является то, что если мы отвергаем нулевую гипотезу , мы не знаем, какие методы лечения можно считать существенно отличающимися от других, а также, если F -тест проводится на уровне α, мы не можем утверждать, что пара методов лечения с наибольшей разницей средних значений существенно отличается на уровне α.

Проблемы регрессии

Рассмотрим две модели, 1 и 2, где модель 1 «вложена» в модель 2. Модель 1 — ограниченная модель, а модель 2 — неограниченная. То есть модель 1 имеет p ₁ параметров, а модель 2 — p ₂ параметров, где p ₁  <  p ₂ , и для любого выбора параметров в модели 1 та же самая кривая регрессии может быть получена некоторым выбором параметров модели 2.

Одним из распространенных контекстов в этом отношении является решение вопроса о том, соответствует ли модель данным значительно лучше, чем наивная модель, в которой единственным объясняющим термином является член-перехват, так что все прогнозируемые значения для зависимой переменной устанавливаются равными выборочному среднему этой переменной. Наивная модель является ограниченной моделью, поскольку коэффициенты всех потенциальных объясняющих переменных ограничены и равны нулю.

Другим распространенным контекстом является решение о наличии структурного разрыва в данных: здесь ограниченная модель использует все данные в одной регрессии, в то время как неограниченная модель использует отдельные регрессии для двух различных подмножеств данных. Такое использование F-теста известно как тест Чоу .

Модель с большим количеством параметров всегда сможет соответствовать данным, по крайней мере, так же хорошо, как и модель с меньшим количеством параметров. Таким образом, обычно модель 2 будет давать лучшее (т. е. меньшую ошибку) соответствие данным, чем модель 1. Но часто хочется определить, дает ли модель 2 значительно лучшее соответствие данным. Один из подходов к этой проблеме — использовать F -тест.

Если имеется n точек данных для оценки параметров обеих моделей, то можно рассчитать F -статистику, заданную как

${\displaystyle F={\frac {\left({\frac {{\text{RSS}}_{1}-{\text{RSS}}_{2}}{p_{2}-p_{1}}}\right)}{\left({\frac {{\text{RSS}}_{2}}{n-p_{2}}}\right)}}={\frac {{\text{RSS}}_{1}-{\text{RSS}}_{2}}{{\text{RSS}}_{2}}}\cdot {\frac {n-p_{2}}{p_{2}-p_{1}}},}$

где RSS _i — остаточная сумма квадратов модели i . Если регрессионная модель была рассчитана с весами, то замените RSS _i на χ ² , взвешенную сумму квадратов остатков. При нулевой гипотезе о том, что модель 2 не обеспечивает значительно лучшего соответствия, чем модель 1, F будет иметь распределение F с ( p ₂ − p ₁ ,  n − p ₂ ) степенями свободы . Нулевая гипотеза отклоняется, если F , вычисленное по данным, больше критического значения F -распределения для некоторой желаемой вероятности ложного отклонения (например, 0,05). Поскольку F — монотонная функция статистики отношения правдоподобия, F -тест является тестом отношения правдоподобия .

Смотрите также

• Качество соответствия

Ссылки

1. Бергер, Пол Д.; Маурер, Роберт Э.; Челли, Джована Б. (2018). Экспериментальный дизайн. Cham: Springer International Publishing. стр. 108. doi : 10.1007/978-3-319-64583-4. ISBN 978-3-319-64582-7.
2. Ломакс, Ричард Г. (2007). Статистические концепции: Второй курс . стр. 10. ISBN 978-0-8058-5850-1.
3. Бокс, GEP (1953). «Ненормальность и тесты на дисперсии». Biometrika . 40 (3/4): 318–335. doi :10.1093/biomet/40.3-4.318. JSTOR  2333350.
4. Марковски, Кэрол А.; Марковски, Эдвард П. (1990). «Условия эффективности предварительного дисперсионного теста». Американский статистик . 44 (4): 322–326. doi :10.2307/2684360. JSTOR  2684360.
5. Sawilowsky, S. (2002). "Fermat, Schubert, Einstein, and Behrens–Fisher: The Probable Difference Between Two Means When σ12 ≠ σ22". Journal of Modern Applied Statistical Methods . 1 (2): 461–472. doi : 10.22237/jmasm/1036109940 . Архивировано из оригинала 2015-04-03 . Получено 2015-03-30 .
6. Siegel, Andrew F. (2016-01-01), Siegel, Andrew F. (ред.), «Глава 15 — ANOVA: Тестирование различий между многими выборками и многое другое», Practical Business Statistics (седьмое издание) , Academic Press, стр. 469–492, doi : 10.1016/b978-0-12-804250-2.00015-8, ISBN 978-0-12-804250-2, получено 2023-12-10

Дальнейшее чтение

• Фокс, Карл А. (1980). Промежуточная экономическая статистика (второе издание). Нью-Йорк: John Wiley & Sons. стр. 290–310. ISBN 0-88275-521-8.
• Джонстон, Джон (1972). Эконометрические методы (второе изд.). Нью-Йорк: McGraw-Hill. С. 35–38.
• Кмента, Ян (1986). Элементы эконометрики (Второе изд.). Нью-Йорк: Macmillan. С. 147–148. ISBN 0-02-365070-2.
• Маддала, GS ; Лахири, Каджал (2009). Введение в эконометрику (Четвертое изд.). Чичестер: Уайли. стр. 155–160. ISBN 978-0-470-01512-4.

Внешние ссылки

• Таблица критических значений F-теста
• Бесплатный калькулятор для F-тестирования
• F-тест для линейной регрессии
• Лекция по эконометрике (тема: проверка гипотез) на YouTube от Марка Тома